Atoms | Physics Notes for IITJEE/NEET

ATOMS

THOMSON'S ATOMIC MODEL

This model suggests an atom to be a tiny sphere of radius, containing the positive charge. The atom is electrically neutral. It contains an equal negative charge in the form of electrons, which are embedded randomly in this sphere, like seeds in a watermelon.

This model failed to explain

• large scattering angle of α-particle
• origin of spectral lines observed in the spectrum of hydrogen atom

ALPHA-PARTICLE SCATTERING AND RUTHERFORD'S NUCLEAR MODEL OF ATOM

In Rutherford α- particle scattering experiment a very fine beam of α-particle passes through a small hole in the lead screen. This well collimated beam is then allowed to fall on a thin gold foil. While passing through the gold foil, α-particles are scattered through different angles. A zinc sulphide screen is placed out the other side of the gold foil, this screen is movable, so as to receive the α-particles, scattered from the gold foil at angles varying from 0 to 180°. When a α-particle strikes the screen, it produces a flash of light.

FINDINGS

• Most of the α-particles went straight through the gold foil and produced flashes on the screen as if there were nothing inside gold foil. This suggests that the most part of the atom is empty.
• Few particles collided with the atoms of the foil which have scattered or deflected through considerable large angles. Very few particles even turned back towards source itself.

CONCLUSIONS

• The entire positive charge and almost whole mass of the atom is concentrated in small centre called a nucleus.
• The electrons revolving round the nucleus could not deflected the path of α-particles. This suggests that electrons are very light.

In 1911 Rutherford, proposed a new type of model of the atom. According to this model, the positive charge of the atom, instead of being uniformly distributed throughout a sphere of atomic dimension is concentrated in a very small volume at its centre. This central core, called nucleus, is surrounded by clouds of electrons makes the entire atom electrically neutral.

According to Rutherford scattering formula, the number of
α-particles scattered at angle θ by a target,

N ∝ cosec4 (θ/2)

Impact parameter

Distance of closest approach

RESULT OF RUTHERFORD SCATTERING EXPERIMENT

Nucleus is central, massive, positively charged core, its size of the order of 10–15 m, number of electrons surrounding nucleus is such that atom is electrically neutral.

Unit for nuclear dimension measurement : 1 fermi = 10–15m.

BOHR’S ATOMIC (HYDROGEN ATOM) MODEL

In 1913 Bohr gave his atomic theory primarily to explain, the spectra of hydrogen and hydrogen-like atoms. His theory, contained a combination of views from Plank’s quantum theory, Einstein’s photon concept and Rutherford model of atom. The Bohr theory can explain, the atomic spectra of hydrogen atom and hydrogen-like ions such as He+, Li2+, Be3+...(one electron ions). But his theory failed to explain, the spectra of more complex atom and ions.

BASIC POSTULATES OF BOHR’S MODEL

1. The electron moves in circular orbits around the nucleus under the influence of coulombic force of attraction between the electron and the positively charged nucleus (as shown in figure below).

Bohr’s model of hydrogen atom

2. The electron rotates about the nucleus in certain stationary circular orbits, for which the angular momentum of electron about the nucleus is an integral multiple of, where h is plank’s constant

i.e., Angular Momentum, ...(1)

(where n = 1, 2, 3......... principal quantum number)

3. When the electron is in one of its stationary orbits, it does not radiate energy, hence the atom is stable. These stationary orbits are called allowed orbits.
4. The atom radiates energy when the electron “jumps” from one allowed stationery state to another. The frequency of radiation follows the condition

hν = Ei – Ef ...(2)

Where Ei and Ef are total energies of initial and final stationary states. This difference in energy (Ei -Ef) between two allowed stationary states is radiated/absorbed in the form of a packet of electromagnetic energy (hν - one photon of frequency ν) called a photon.

Now we calculate the allowed energies of hydrogen atom,

For moving an electron in a circular orbit the required centripetal force is provided by the coulomb force of attraction which acts between nucleus [Ze+, here Z = 1 (atomic number) for hydrogen atom] & electron (e–),

i.e., ...(3)

where is electrostatic constant & εo is permittivity of free space.

Eliminating v from eqn. (1) and (3) we obtain radius of nth orbit

(where n = 1, 2, 3 .....) ...(4)

Equation (4) gives the radii of various orbits (have discrete values).

The smallest radius (also called Bohr radius) corresponds to n = 1 is

...(5)

⇒ r = 0.529 n2 Å for hydrogen atom and

r = 0.529 × for hydrogen like ions.

From equation (4) & (1) we obtain,

Velocity of electron in nth state

or  (for hydrogen atom ) ...(6)

  for hydrogen like ions

The total energy of electron is given by

E = K.E. + P.E. = Kinetic energy + Potential energy

   

...(7)  

(Allowed energy state)

After substituting numerical values in eqn.(7), we obtain

   (for hydrogen atom) ...(8)

(for hydrogen like ions)

The lowest energy state, or ground state, corresponds to n = 1 is

The next state corresponds to n = 2 i.e., first excited state has an energy, E = –3.4 eV

LIMITATIONS OF BOHR'S MODEL

• It could not explain the spectra of atoms containing more than one electron.
• There was no theoretical basis for selecting mvr to be an integral multiple of .
• It involved the orbit concept which could not be checked experimentally.
• It could not explain Zeeman & Stark effect and fine lines of spectra.
• It was against de-Broglie concept and uncertainty principle.

KEEP IN MEMORY

1. Total energy of electron = – Kinetic energy

2. The reference level for potential energy has been taken as infinity
3. The energy gap between two successive levels decreases as the value of n increases
4. The  radius difference between the successive orbit (or shells) increases as the value of n increases
5. The velocity of electrons around the nucleus goes on decreasing as n increases
6. The time period of the electron in an orbit
7. Maximum number of spectral lines that can be emitted when an electron jumps from nth orbit is

ENERGY LEVELS AND THE LINES SPECTRA OF HYDROGEN ATOM

An energy level diagram of the hydrogen atom is shown in figure. The upper most level corresponding to n→, represents the state for which the electron is completely removed from the atom.

Some transitions for Lyman, Balmer & Paschen series are shown. The quantum numbers are at left & energies of levels are at right.

E = 0 for r = (Since  n = )

If the electron jumps from allowed state ni to allowed state nf, then frequency of emitted photon is given by

...(1)

and the wavelength of emitted photon is

for hydrogen atom ...(2)

and ( for H-like atoms)

where R = 1.096776 × 107m–1 is known as Rydberg constant. By using this expression we can calculate the wavelengths for various series (Lyman, Balmer...) in hydrogen spectrum, i.e.

1. Lyman series ni = 1 & nf = 2, 3, 4...............
2. Balmer series ni = 2, & nf = 3, 4, 5...............
3. Paschen series ni = 3 & nf = 4, 5, 6..............
4. Brackett series ni = 4 & nf = 5, 6, 7...............
5. P fund series ni = 5 & nf = 6, 7, 8...............

First three series of hydrogen atom are shown in figure.

But in practice, the value of Rydberg constant varies between and R

This is because in above calculations we assumed that electron revolves around a massive fixed nucleus of mass M. But in reality, the electron and nucleus each revolve round their common center of mass i.e., the motion of nucleus cannot be ignored. The correction for nuclear motion amounts to replacing electronic mass m by reduced mass μ which is defined as

...(3)

So total energy by taking this correction is

...(4)

If we are dealing with hydrogen like ions such as – He+, Li2+, Be3+, Be4+ (one electron ions), each can be considered as a system of two charges, the electron of mass m & charge –e & nucleus of mass M and charge +Ze, where Z is atomic number. The radii of circular orbits for these one electron ions can be written as

(n = 1, 2, 3............) ...(5)

and the allowed energies are given by

  (n = 1, 2, 3.........) ...(6)

WAVELENGTH LIMITS IN VARIOUS SPECTRAL SERIES OF HYDROGEN ATOM

1. For Lyman series (lies in ultraviolet region)

Here  

2. For Balmer series (lies in visible region)

Here

3. For Paschen series (lies in infrared region)

Here

4. For Brackett series (lies in infrared region)

Here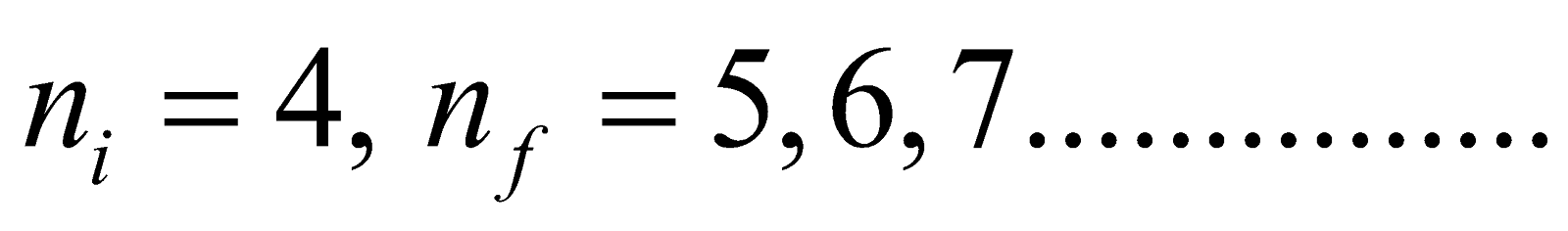

5. For p-fund series (lies in infrared region)

Here

KEEP IN MEMORY

1. The first line of Lyman series is when electron jumps from 2 → 1, It is also called α–line

The second line of lyman series is when electron jumps from 3 → 1, It is also called β–line

The limiting line of lyman series is when electron jumps from ∞ → 1

2. Energy of electrons in different orbits in an atom varies inversely with the square of the number of orbits. So, energy of electrons increases (decreases in negative) as the orbit becomes higher.
3. If energy of a particular orbit is E for H-atom then its value for a H-like atom with atomic number Z is given by E' = E × Z2.
4. If the radius of a particular orbit of H-atom is R then its value for a H-like atom is given by

5. If velocity of an electron in a particular orbit of H-atom be v then its value for H-like atom is given by

v'= v × Z.

6. If kinetic energy and potential energy of an electron in a particular orbit of H-atom be T and V respectively then their corresponding values for  H-like atom are given by
   T' = T × Z2  and  V' = V× Z2.

COMMON DEFAULT

🗶 Incorrect.  Bohr's formula for spectral lines does not differentiate between isotopes. For example the first line of Lyman series in hydrogen and deuterium will have same wavelength because

✔ Correct. The value of R will be different for hydrogen and deuterium and therefore λ will be different for the two cases. In fact

Physics Study Notes

• Physical World
• Units and Measurements
• Motion in a Straight Line
• Motion in a Plane
• Laws of Motion
• Work, Energy and Power
• System of particles and Rotational Motion
• Gravitation
• Mechanical Properties of Solids
• Mechanical Properties of Fluids
• Thermal Properties of Matter
• Thermodynamics
• Kinetic Theory of Gases
• Oscillations
• Waves
• Electric Charges and Fields
• Electrostatic Potential and Capacitance
• Current Electricity
• Moving Charges and Magnetism
• Magnetism and Matter
• Electromagnetic Induction
• Alternating Current
• Electromagnetic Waves
• Ray Optics and Optical Instruments
• Wave Optics
• Dual Nature of Radiation and Matter
• Atoms
• Nuclei
• Semiconductor Electronics : Materials, Devices and Simple Circuits
• Communication Systems
• Experimental Skills in Physics

Study Notes for JEE Main/JEE Advanced

Study Notes for NEET/AIIMS