EXPERIMENTAL SKILLS IN PHYSICS
LEAST COUNT AND ZERO ERROR
The magnitude of the smallest measurement that can be measured by an instrument accurately is called its least count (L.C.).
The difference between one main scale division (M.S.D.) and one vernier scale division is called least count.
i.e. L.C. = One M.S.D. – One V.S.D.
ZERO ERROR
If there is no object between the jaws (i.e., jaws are in contact), the vernier should give zero reading. But due to some extra material on jaws, even if there is no object between the jaws, it gives some excess reading. This excess reading is called zero error.
Zero correction : Zero correction is invert of zero error.
Zero correction = – (Zero error)
Actual reading = observed reading – excess reading (zero error)
= observed reading + zero correction
= observed reading + zero correction
EXPERIMENT 1
AIM
To measure the internal and external diameter and depth of a vessel using a vernier callipers.
THEORY
If with the body between the jaws, the zero of vernier scale lies ahead of Nth division of main scale, then main scale reading (M.S.R.) = N
If with division of vernier scale coincides with any division of main scale, then vernier scale reading (V.S.R.)
= n × (L.C.) (L.C. is least count of vernier callipers)
= n × (V.C.) (V.C. is vernier constant of vernier callipers)
And total reading, T.R. = M.S.R. + V.S.R. = N + n × (V.C.)
DESCRIPTION
First calculate the least count of vernier callipers by the formula L.C. = 1 M.S.D. – 1 V.S.D.
For a standard vernier callipers, the least count is 0.1 mm or 0.01cm. Now find the zero error and check it is positive or negative. The zero error is positive if the zero of vernier scale lies to the right to the zero of main scale and negative if the zero of vernier scale lies to the left to the zero of main scale. Let nth division of vernier scale coincides to the zero of main scale then multiply n by least count and put positive sign if zero error is positive and put negative sign if zero error is negative. Now add the zero error with sign opposite to the observation.
To measure the internal diameter, use upper jaws of vernier callipers. Note main scale reading and find the number of division on vernier scale which matches with main scale division and multiply it with least count and add it to main scale reading to get the internal diameter.
To measure the external diameter, use lower jaws of vernier callipers. Note the reading and get the external diameter.
To measure the depth of vessel, use the sliding strip of vernier callipers. Put the edge of the main scale of the vernier callipers on the mouth of the vessel, in such a way that the strip R is able to go inside the vessel along its depth. Move the sliding jaw so that the strip R touches the bottom of vessel. Read the observations as above and get the depth of vessel.
PRECAUTIONS
- Make the motion of vernier scale on main scale very smooth (by oiling).
- Find the vernier constant and zero error carefully and record them properly.
- Grip the body between the jaws formerly but gently.
- Take atleast observation at three different places at right angles at each place.
- No parallax should be there.
EXPERIMENT 2
AIM
To determine thickness/diameter of thin sheet/wire using a Screw Gauge.
THEORY
If with the wire between plane faces A and B, the edge of the cap lies ahead of Nth division of linear scale.
Then, linear scale reading (L.S.R.) = N
If nth division of circular scale lies over reference line, then circular scale reading (C.S.R.) = n × L.C. (L.C. is least count of screw gauge)
Total reading, T.R. = L.S.R. + C.S.R. = N + n × (L.C.)
First calculate the pitch of screw gauge.
Pitch = 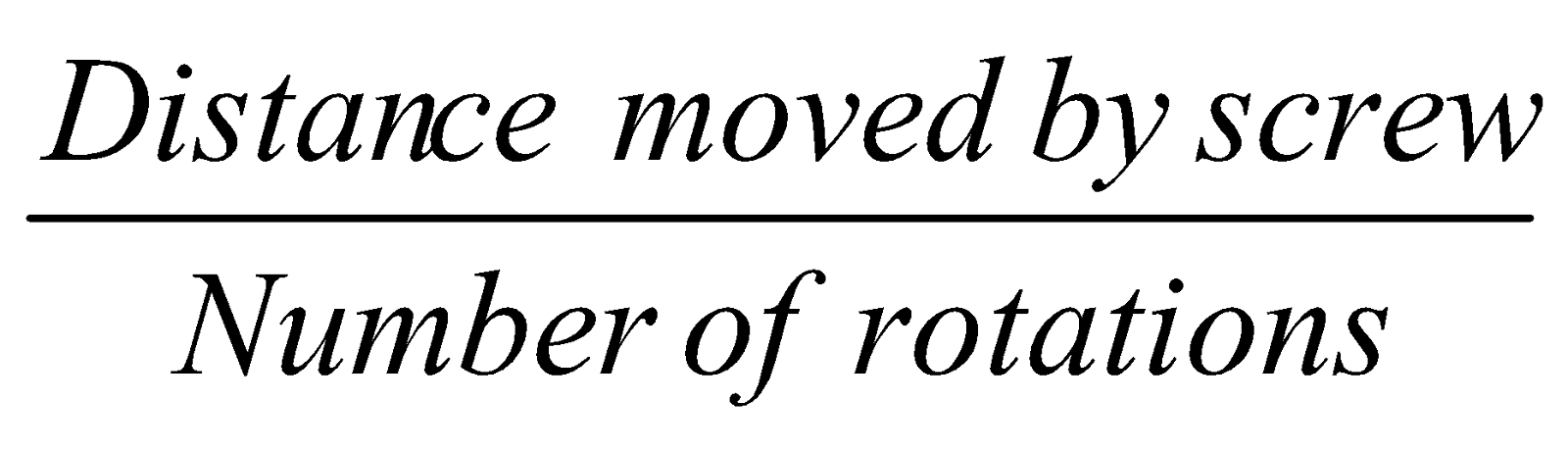
Note the total number of divisions on the circular scale, then
Least count (L.C.) = 
To find zero error, screw up until the gap between jaws is just closed and ratchet arrangement gives a click. If zero division of the circular scale coincides with the reference line, then there is no zero error, if reference line may be x divisions towards positive side of zero, then zero error is + x × L.C. and if negative side then zero error is – x × L.C.
DESCRIPTION
To find the thickness of sheet, place it between the gaps and turn screw head. Note the reading of main scale and no. of divisions of the circular scale coinciding with reference line. If the reading of main scale is x mm and yth division coincides, then total reading is (x + y × L.C.) mm.
To find the diameter of wire, place the wire between the gaps and take different observations as above and find the diameter.
PRECAUTIONS
- Always rotate the screw by the ratchet and not by the cap.
- The screw should move freely without friction.
- Note the zero correction properly (with sign).
- Avoid backlash error of the screw by moving it in the same direction for same set of observations.
- Measure the diameter into two perpendicular directions at each place.
- Avoid parallax error.
EXPERIMENT 3
AIM
To study conservation of energy at different positions while a simple pendulum is oscillating.
MATERIAL REQUIRED
A thin wire, tension screw fixed to a rigid support in ceiling a metallic block, bob, ticker timer, paper tape, metre scale and thread.
THEORY
When a simple pendulum oscillates then at mean position it has kinetic energy and at extreme position it has potential energy and at different intermediate positions it has both types of energies.
Here, h = 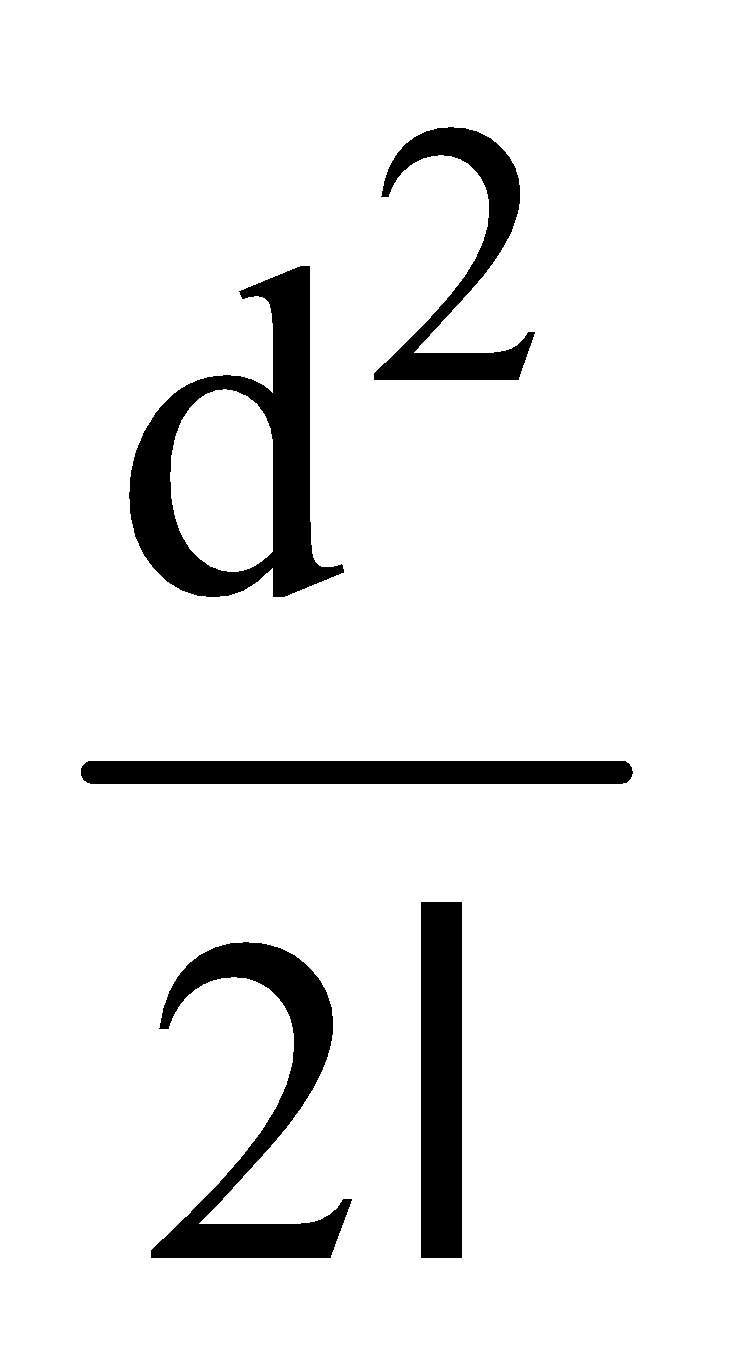 .
.
KE at E =  mv2; P.E at
mv2; P.E at
E = mgh = mg
Total energy = 
DESCRIPTION
It obeys the law of conservation of energy. Clamp the wire with ceiling, suspend metallic block as shown in diagram. Paste paper tape from carbon of ticker timer and attach one end to the centre of block. Tie a thread at C.G of block. Pull the thread towards ticker timer and leave it. It oscillates and pulls the paper tape and dots are obtained. Observe the paper tape.
Distance of dots from central dot (A) = d
Time period of ticker timer = 0.01 sec. Draw table for d, t, v, h, KE and PE and total energy and draw graph shown as:
We observe that the energy conservation law holds good.
PRECAUTIONS
- Carefully take the readings.
- Clamp the wire tightly with ceiling.
EXPERIMENT 4
AIM
To measure the mass of a given object by the principle of moments using a metre scale.
MATERIAL REQUIRED
A set of known masses, metre scale and an unknown mass.
THEORY
If m and M be the mass of the body and mass of the weight used and a1 and a2 be the distances of their loops from wedge. Then, power (mass) arm = a1, weight arm = a2
From principle of moments mg a1 = Mg a2
or  which can be calculated.
which can be calculated.
DESCRIPTION
Metre scale is hang by a thread to a peg so that it is in horizontal position. The principle is that whenever two equal and opposite forces act at a perpendicular distance, then they form a couple and hence a torque is applied.
Torque = either force × perpendicular distance between two forces
Here, metre scale is hung at its centre of gravity, a known mass is attached at one side of centre of gravity and attach an unknown weight on other side of centre of gravity and adjust its distance from centre of gravity, such that the metre scale becomes horizontal. Now apply the formula for torque after measuring the distances from C.G.
M × x = m × y
PRECAUTIONS
• Use a broad and heavy wedge with sharp edge.
• Metre scale should have uniform mass distribution.
• Threads used for loops should be thin, light and strong.
EXPERIMENT 5
AIM
Determination of Young's modulus of elasticity of the material of a metallic wire.
MATERIAL REQUIRED
Searle's apparatus with steel wire, screw gauge, metre rod and weight.
THEORY
If a wire of length L and radius r be loaded by a weight Mg and if l be the increase in length, then,
Normal stress =  and longitudinal strain
and longitudinal strain 
Hence, Young's modulus (Y) 
or 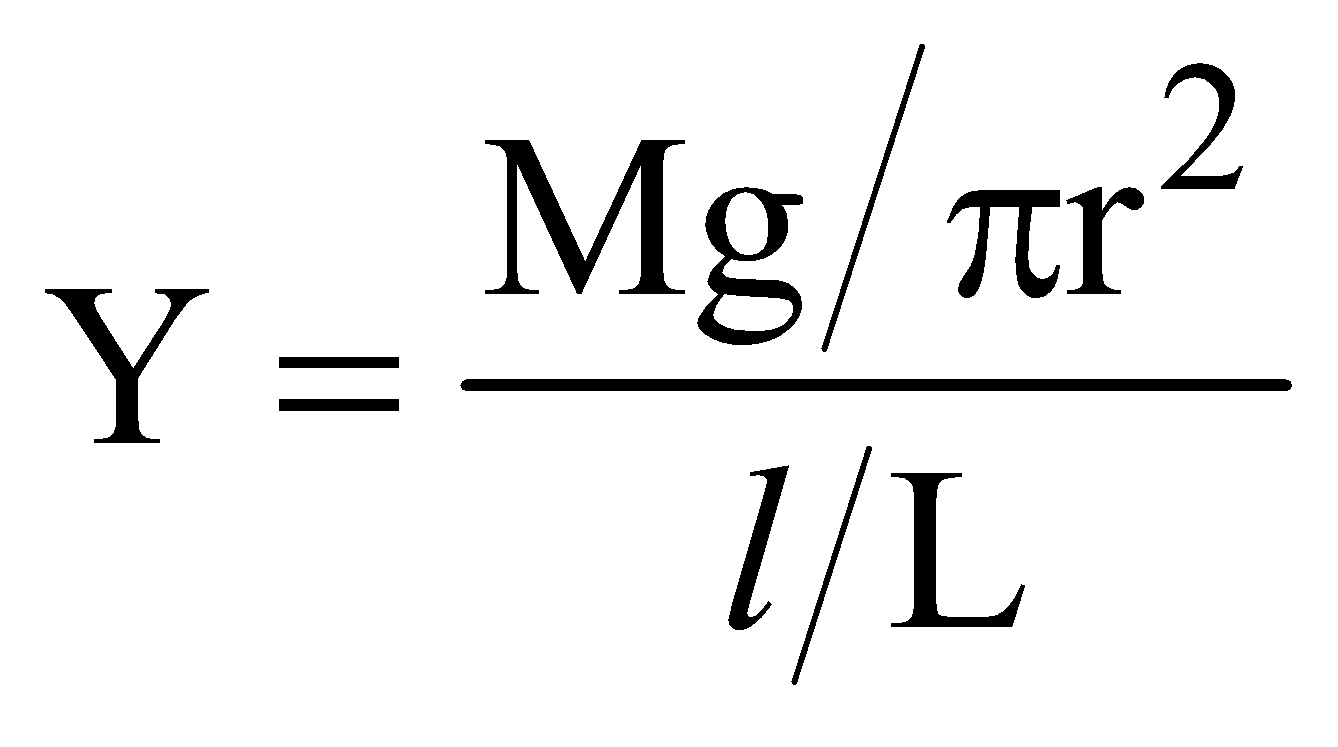 or
or 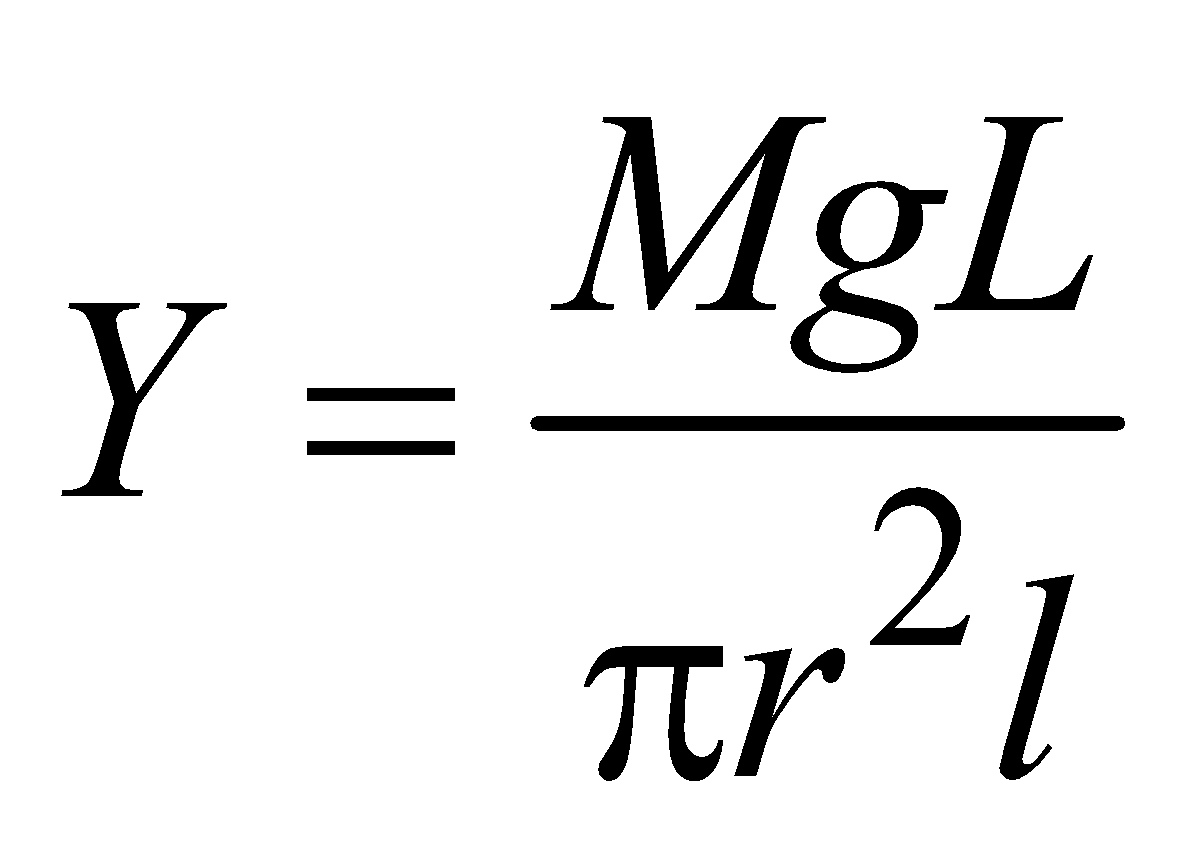
Knowing L and r, and finding l for known Mg, Y can be calculated.
Mg = wt. suspended; L = original length of the wire; r = radius of the wire; l = change in length of wire
DESCRIPTION
First, calculate the diameter of the wire with the help of screw gauge. Now, determine the pitch and least count of micrometer screw. Hang a hanger 'H' in the hook B and connect to experimental wire b. Suspend a weight W from the other hook.
Searle's apparatus
Now calculate the breaking load by formula
Breaking load = Breaking stress × area of cross-section.
Place gently half kg wt in H and wait for few minutes, so that the wire extends and note the reading of micrometer screw. Repeat the experiment for more weights. Now unload the hanger. Take the reading for extension when weight loaded or unloaded is 2kg. Find mean extension and by using formula
Calculate the value of Young's modulus of material of wire.
PRECAUTIONS
- The wires (both experimental and auxiliary) should be of same length, material and thickness.
- They must be supported from the same rigid support.
- Kinks should be removed from the experimental wire.
- Measure the diameter of the wire at different places and along two mutually perpendicular directions at every place.
- Add and remove weights gently and slowly.
EXPERIMENT 6
AIM
Calculation of surface tension of water by capillary rise and effect of detergents.
MATERIAL REQUIRED
Tubes of different radii, a pointer, metallic plate, travelling microscope, open dish, thermometer etc.
THEORY
Let the liquid rise upto a height h (as measured for the lower meniscus B) and let the meniscus ABC have hemispherical shape [Fig. (b)].
Then, volume of the liquid risen upto lower meniscus = πr2h
Volume of liquid in meniscus above B.
= Volume of cylinder of radius r – Volume of hemisphere of radius r
Water level rising in a glass capillary tube
Total volume of the liquid risen
If liquid has a density ρ, then, mass of liquid risen 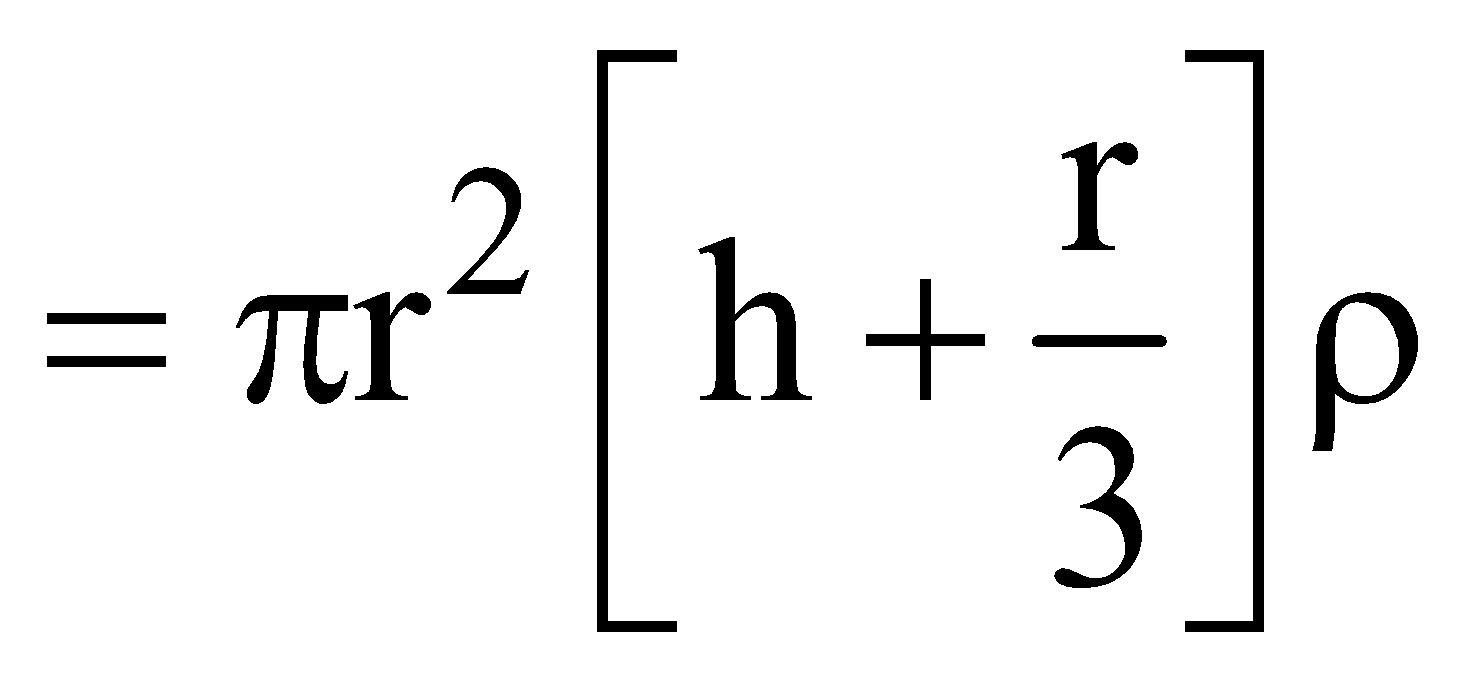
and weight of the liquid risen 
For equilibrium,
or 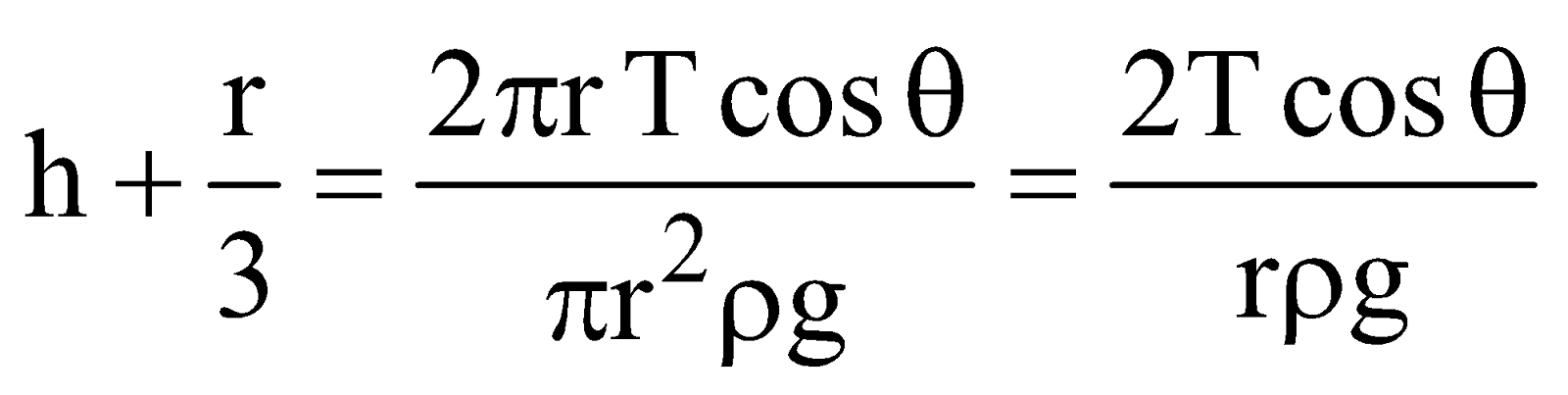
or 
[From above we find that 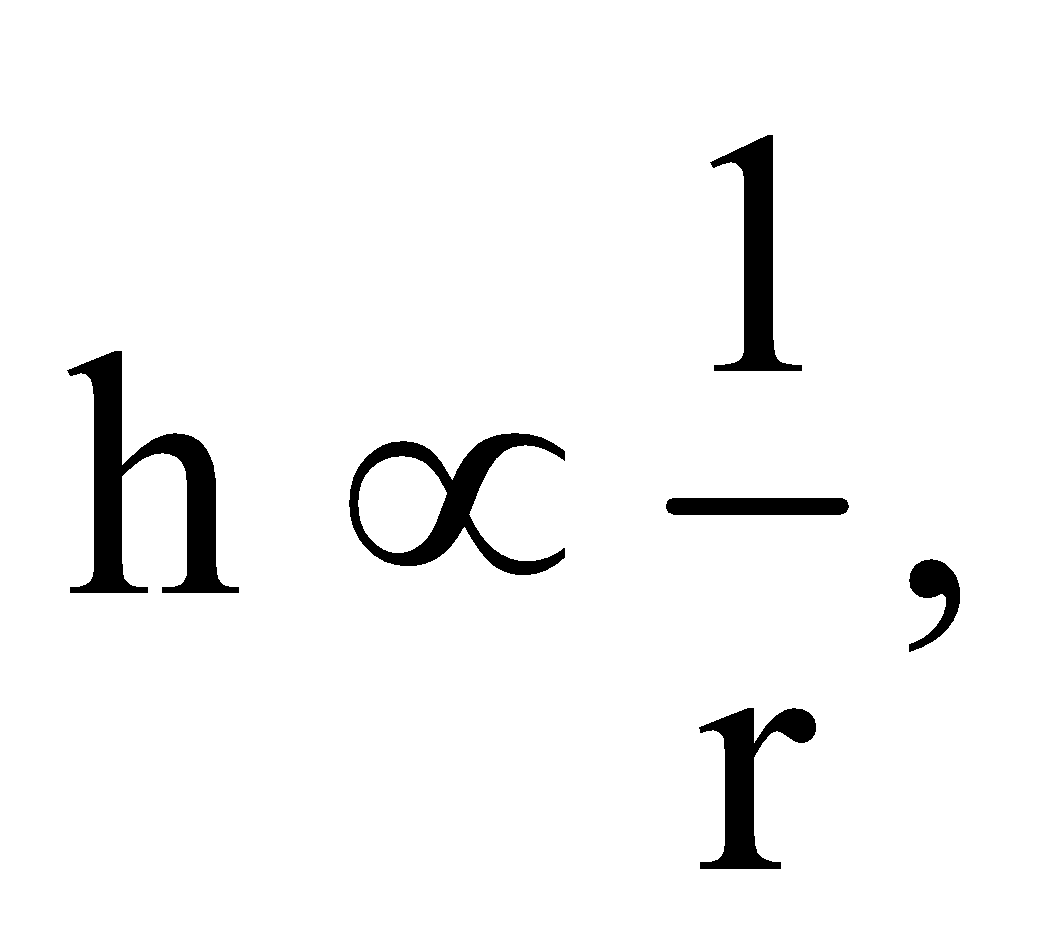 liquid rises more in capillary tube of small radius]
liquid rises more in capillary tube of small radius]
Also, 
Measuring height h of liquid risen in capillary tube and knowing other quantities, surface tension of liquid (T), can be calculated.
[In practice,  is neglected as compared to h, then
is neglected as compared to h, then ]
]
Description : Set the apparatus as shown in diagram.
Measurement of surface tension by capillary rise
Calculate least count of travelling microscope, raise the microscope to a suitable height and bring in front of first tube. Now make the cross-wire just touch the central part of the concave meniscus note the reading of vertical scale and do same for second and third tube. Now move the microscope horizontally so as to bring infront of the pointer. Find the difference in the readings and calculate h.
Now to calculate the internal diameter of capillary tube place the tube horizontally on the adjustable stand. A white circle (inner bore) surrounded by a green circular strip is to be seen (glass cross-section).
Make horizontal crosswire touch the inner circle at A and note the reading.
Now raise the microscope so that the cross wire touches the circle at B. Note the reading. Difference gives the internal diameter AB. Note the temperature of water.
Internal radius = 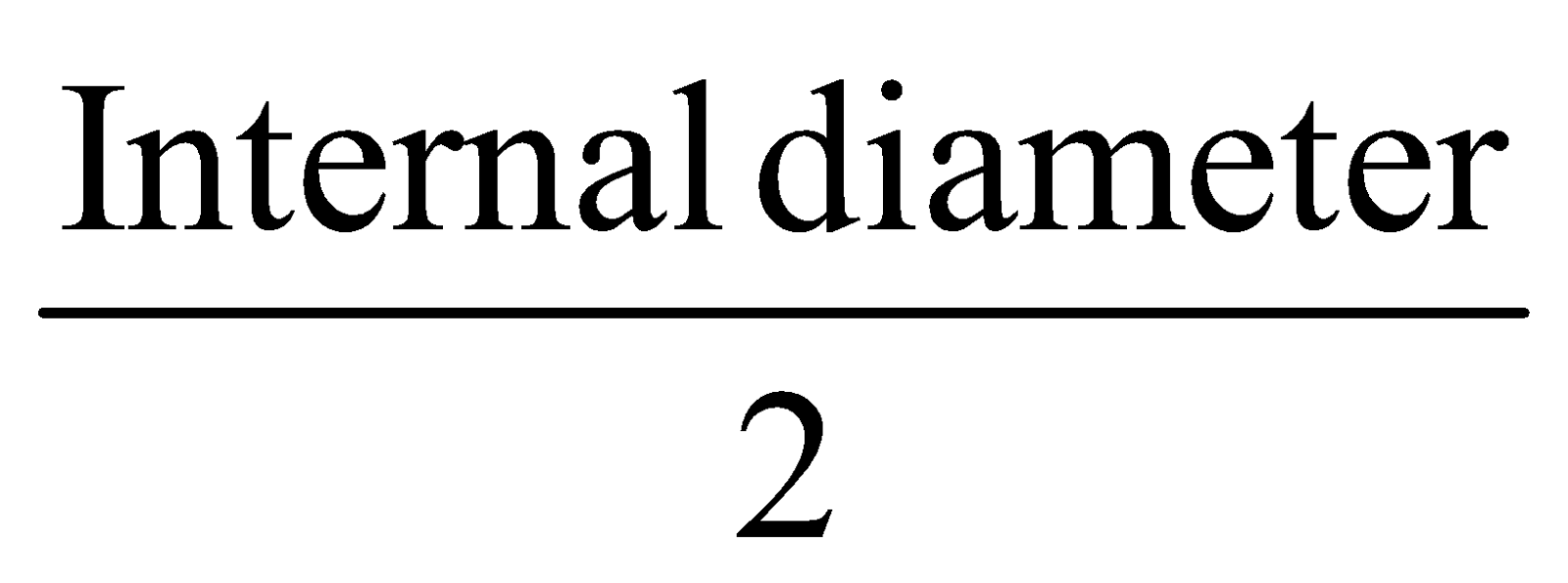
and 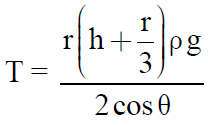 can be calculated.
can be calculated.
For water : θ = 8° ; cos θ = 0.99027 taken as 1
If we dissolve some amount of detergent to water then rise of water will be less than that for pure water. As we increase more and more detergent then level will go down and thus surface tension decreases.
PRECAUTIONS
- Capillary tube and water should be free from grease.
- The tube should be set properly.
- Vertical microscope should be moved in lower direction only to avoid backlash error.
- Keep a note of the temperature of water.
- Measure the internal diameter of the capillary tube in two mutually perpendicular directions.
EXPERIMENT 7
AIM
Calculation of coefficient of viscosity of a given viscous liquid by measuring terminal velocity of a given spherical body.
MATERIAL REQUIRED
A beaker or jar, screw gauge, viscous liquid. steel ball, glycerine and paper clip.
THEORY
We know that the terminal velocity
where , r = radius of spherical body
ρ = density of solid
ρ = density of solid
σ = density of liquid
v = terminal velocity
v = terminal velocity
η = coefficient of viscosity.
DESCRIPTION
Take a wide glass jar and filled with glycerine. Paste some paper strip round the jar. Take some steel balls and measure their diameter with screw gauge. Roll the steel balls into the liquid and after covering some distance start the stopwatch and note the time of falls between two slips (paper). Repeat the experiment four times and put the value of terminal speed = and find the value of coefficient of viscosity.
and find the value of coefficient of viscosity.
Take a wide glass jar and filled with glycerine. Paste some paper strip round the jar. Take some steel balls and measure their diameter with screw gauge. Roll the steel balls into the liquid and after covering some distance start the stopwatch and note the time of falls between two slips (paper). Repeat the experiment four times and put the value of terminal speed =
PRECAUTIONS
- Liquid should be transparent to watch the motion of the ball.
- Ball should be perfectly spherical.
- Note the velocity only once it becomes constant.
EXPERIMENT 8
AIM
To plot a cooling curve for the relationship between the temperature of a hot body and time.
To plot a cooling curve for the relationship between the temperature of a hot body and time.
MATERIAL REQUIRED
Newton's law of cooling apparatus,two thermometers, clamp and stopwatch.
THEORY
According to Newton's law of cooling, rate of cooling ∝ difference of temperature of body and surrounding.
i.e.,  ;
;  ∝ (θ-θ0)
∝ (θ-θ0)
so, 
DESCRIPTION
Set the apparatus as shown in diagram.
Newton's law of cooling apparatus
Fill the calorimeter with two third of water at 80°C. Now, find least count of calorimeter. Set the stop watch at zero and note the temperature of water in enclosure. Start stirring the water in calorimeter to cool uniformly and start the stopwatch. Take the temperature of water after every minute. Draw a graph between temperature (°C) and time (min) which is shown as
First temperature decreases fastly and then slowly.
PRECAUTIONS
- Use double walled enclosure to maintain surrounding at a constant temperature.
- Stirring should remain continuous for uniform cooling.
EXPERIMENT 9
AIM
To determine the speed of sound in air at room temperature using a resonance tube.
PRINCIPLE
The resonance tube works on the phenomenon of resonance of air column.
THEORY
Let l1 and l2 be the length of the air column for the first and the second resonance respectively with a tuning fork of frequency ν then, λ = 2(l2– l1)
From relation, 
⇒ v = ν 2(l2 – l1) [Putting the value of λ]
⇒ v =2ν(l2 –l1) , which can be calculated.
If t be the temperature of the air in air column of the resonance tube
Then from formula,
Here v is the average velocity which can be calculated by taking the average of two observed velocities.
Resonance tube
OBSERVATIONS
Temperature of air in column :
(a) In the beginning, t1 = .......°C
(b) At the end, t2 = .......°C
Mean temperature, 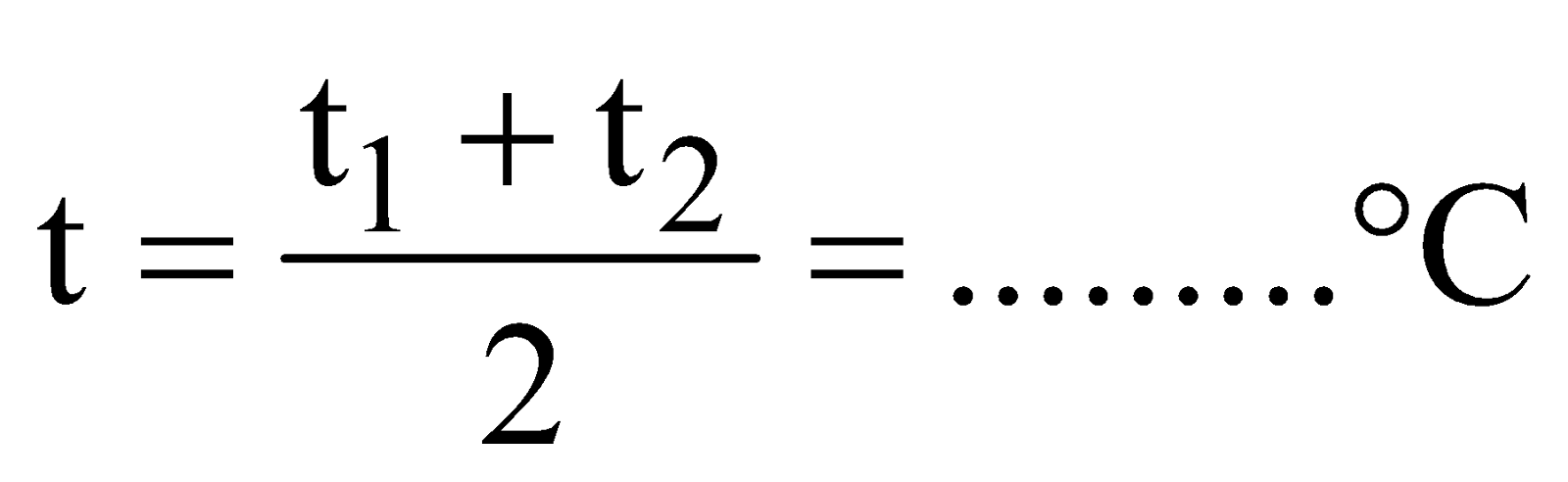
Frequency of first tuning fork, ν1 = 512 Hz
Frequency of second tuning fork, ν2 = 480 Hz
Table for resonant length of air column
Once these observations are made, the velocities at the two frequencies can be calculated. The average of these two velocities will give as v0 can be calculated by the following formula.
% error 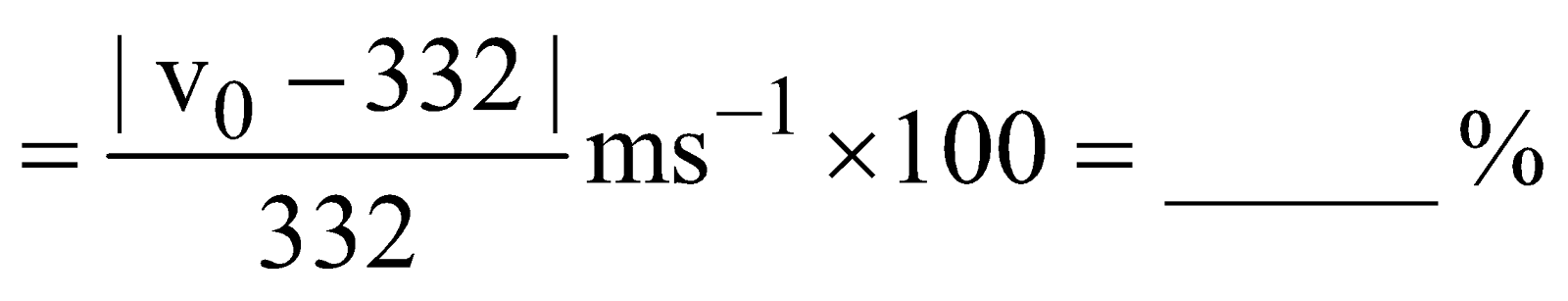
[Actual velocity of sound in air at 0°C = 332 ms –1]
PRECAUTIONS
- Keep the resonance tube vertical and pinch cock tight.
- Vibrate the tuning fork gently by a rubber pad.
- Prongs should be vibrated in a vertical plane above the mouth (end) of the metallic tube and it should not touch it.
- Note the reading for water level falling and rising using a set square.
- While measuring the air temperature, thermometer bulb should not touch water or sites of the resonance tube.
EXPERIMENT 10
AIM
Determination of specific heat capacity of a given (a) solid (b) liquid by method of mixtures.
MATERIAL REQUIRED
A calorimeter, a metal piece, water, thermometer, balance, burner etc.
THEORY
Firstly measure the mass of metal piece heated upto temperature T1. Now drop metal piece into known mass of water in copper calorimeter whose initial temperature is T2 (T2< T1). After stirring sometime the temperature of mixture becomes T. The specific heat of water is known i.e., in M.K.S. system 4200 J/kg°C. So, according to the principle of calorimetry,
Heat lost by metal piece = Heat gained by water
m1c1(T1 – T) = m2c2(T – T2)
so, 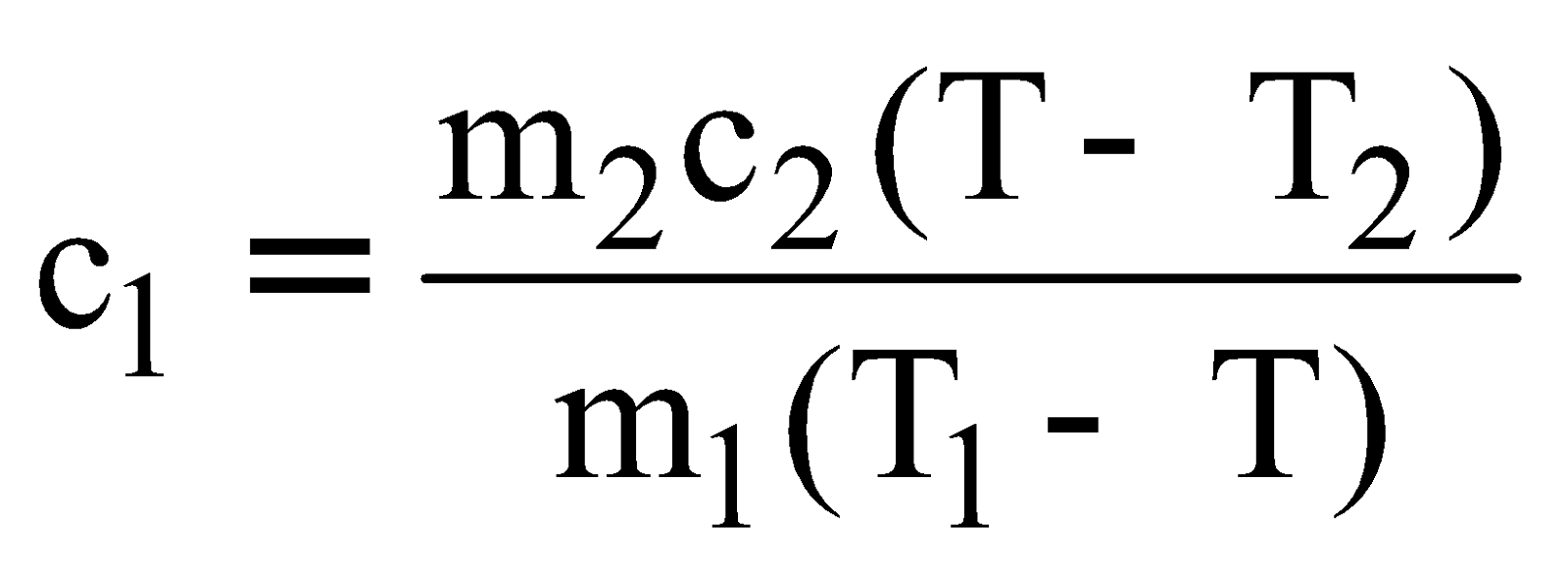
where, m1 = mass of metal
m2 = mass of water
c2 = specific heat of water
T = temperature of mixture
Similarly, we calculate the specific heat of liquid, which is non-reactable.
PRECAUTIONS
- Take the reading of thermometer carefully.
- Stirring should remain continuous
EXPERIMENT 11
AIM
To determine the resistance and resistivity of the material of a given wire using metre bridge.
MATERIAL REQUIRED
A meter bridge, wire whose resistivity is to be measure, battery, etc.
THEORY
- For Resistance : Let AB = cm, then BC = (100 – )
As the metre bridge wire AC has uniform material density and area of cross-section.
Metre bridge
Its resistance is proportional to its length. Hence AB and BC are the ratio arms and their resistances correspond to resistances P and Q, respectively.
Thus, 
where σ is the resistance per unit length (cm) of the bridge wire.
Hence, according to Wheatstone's bridge principle
So knowing R and l, unknown resistance X can be determined.
- For Specific Resistance : From resistance formula
For a wire of radius r or diameter D = 2r
DESCRIPTION
Slide wire bridge or metre bridge is the practical form of Wheatstone bridge. Since the bridge uses 1 metre long wire, it is called metre bridge and a jockey is slided over the wire, it is called a slide wire bridge.
OBSERVATIONS
PRECAUTIONS
- The connections should be neat, clean and tight.
- Move the jockey gently over the bridge wire and do not rub it.
- Introduce a high resistance box in series or a low resistance shunt in parallel with the galvanometer to save the sensitive galvanometer from high current.
- When taking the observation, close the box or open the shunt.
- The plug in the key should be inserted only when the observations are to be taken.
- Keep the null point between 40 cm and 60 cm.
- Use set square to note null point to avoid parallax error.
- Measure the diameter of the wire in two mutually perpendicular directions at one place.
- The wire should not make a loop.
EXPERIMENT 12
AIM
To determine the resistance of a given wire using Ohm's law.
MATERIAL REQUIRED
Ammeter, voltmeter, rheostat, battery and wire whose resistance is to be determined.
THEORY
If V is the potential difference between the two ends of a conductor and I be the current flowing through it, then
V ∝ I or V = IR
where R is the resistance of the conductor.
If we plot a graph of potential difference (V) along Y-axis and current (I) along X-axis then we get a straight line passing through the origin. From the slope of the graph we can calculate the resistance of the wire.
Slope = 
OBSERVATIONS
PRECAUTIONS
- The connections should be neat, clean and tight.
- Use thick copper wires for the connections after removing the insulations near their ends by sand paper.
- The range of the ammeter and voltmeter should be proper.
- Use a low resistance rheostat.
- The unknown resistance should not be too low (much lower than the internal resistance of the battery).
- The key should be inserted only while taking observations to avoid heating of resistance (otherwise its resistance will increase).
EXPERIMENT 13 (A)
AIM
To compare the e.m.f's of two primary cells using a potentiometer.
MATERIAL REQUIRED
Galvanometer, ammeter, rheostat, potentiometer and two primary cells.
PRINCIPLE
It works on the principle that when a current flows through a wire of uniform thickness and material, potential difference between its two points is directly proportional to the length of the wire between the two points.
i.e., 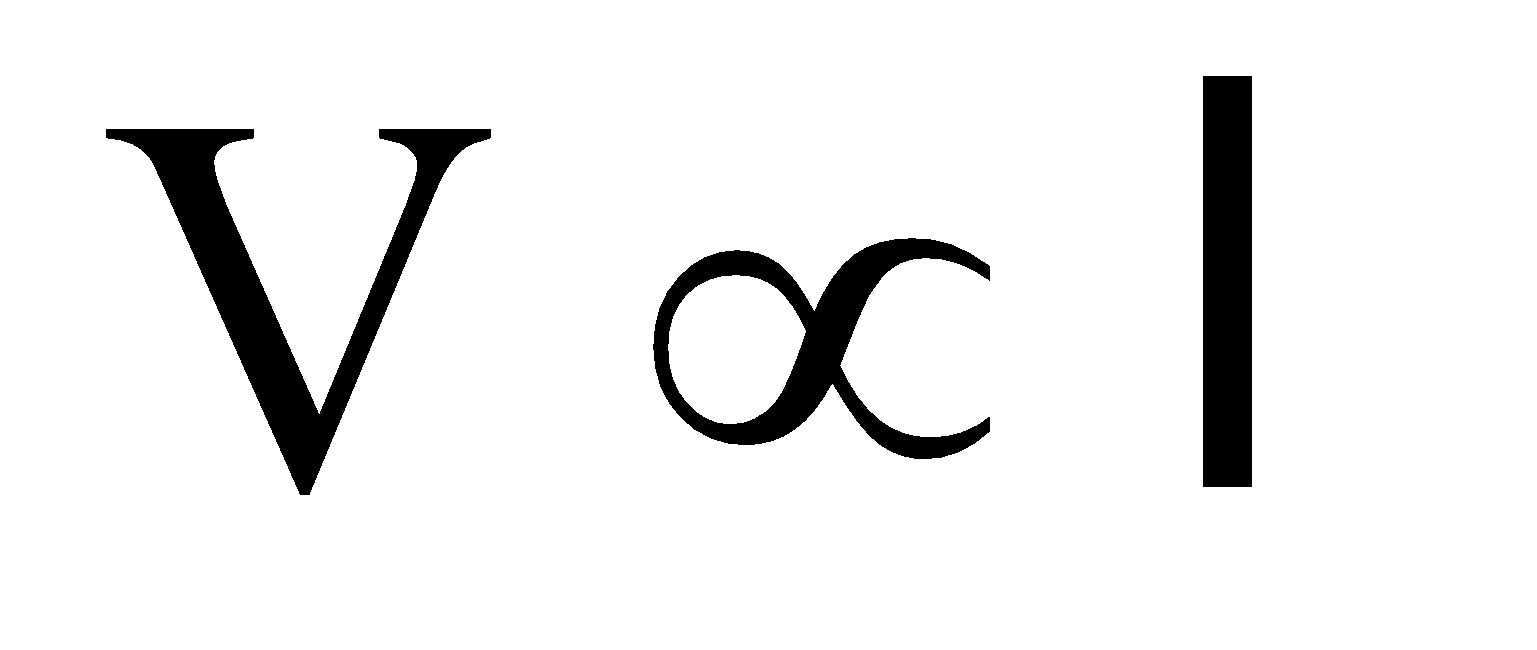 or V = kl
or V = kl
where k is constant of proportionality. It is called 'Potential gradient' along the potentiometer wire.
THEORY
If the null point is at J1 at a distance l1 from A for balancing the e.m.f E1 then
E1 = kl1 ........(i)
If the e.m.f of cell E2 is balanced by the potentiometer wire of length l2 with a balance point at J2 then
E2 = kl2 ∴
Since the galvanometer shows no deflection at the null point so, no current is drawn from the experimental cell and it is thus the actual e.m.f of the cell. First the key K1 is put and null point J1 is noted and then the key K2 is put and null point J2 is noted.
OBSERVATIONS
PRECAUTIONS
- The connections should be neat, clean and tight.
- Introduce the plugs in the key only while taking observations.
- The positive polls of the battery and the cells should all be connected to the terminal at the zero of the wires.
- The e.m.f. of the battery should be greater than the e.m.f.’s of the either of the two cells.
- Do not rub the jockey key along the wire, it should touch the wire gently.
- The ammeter reading should remain constant for a particular set of observations. If necessary, adjust the rheostat for this purpose.
- Use only a low resistance rheostat.
EXPERIMENT 13 (B)
AIM
Comparison of internal resistance of a cell by potentiometer.
MATERIAL REQUIRED
Galvanometer, ammeter rheostat, potentiometer and cells.
THEORY
Let J is the null point and AJ = l1 when cell L is in open circuit (R2 is open). J' is the null point and AJ' = l2 when K2 is closed.
Then E = kl1 V = kl2
OBSERVATIONS
PRECAUTIONS
- Current should be passed for short time only while finding the null point.
- Rheostat should be adjusted so that initial null point lies of last wire of the potentiometer.
- The cell should not be disturbed during experiment.
- Jockey should not be rubbed against the potentiometer wire.
EXPERIMENT 14
AIM
To determine the resistance and figure of merit of a galvanometer by half deflection method.
MATERIAL REQUIRED
Resistance box, galvanometer, battery etc.
THEORY
When K1 is closed and K2 is open, the current Ig through the galvanometer
When K2 is closed, current through the galvanometer,
I'g =
I'g =
Figure of merit (k) can be calculated by the relation,
Ig = k θ ⇒ k = 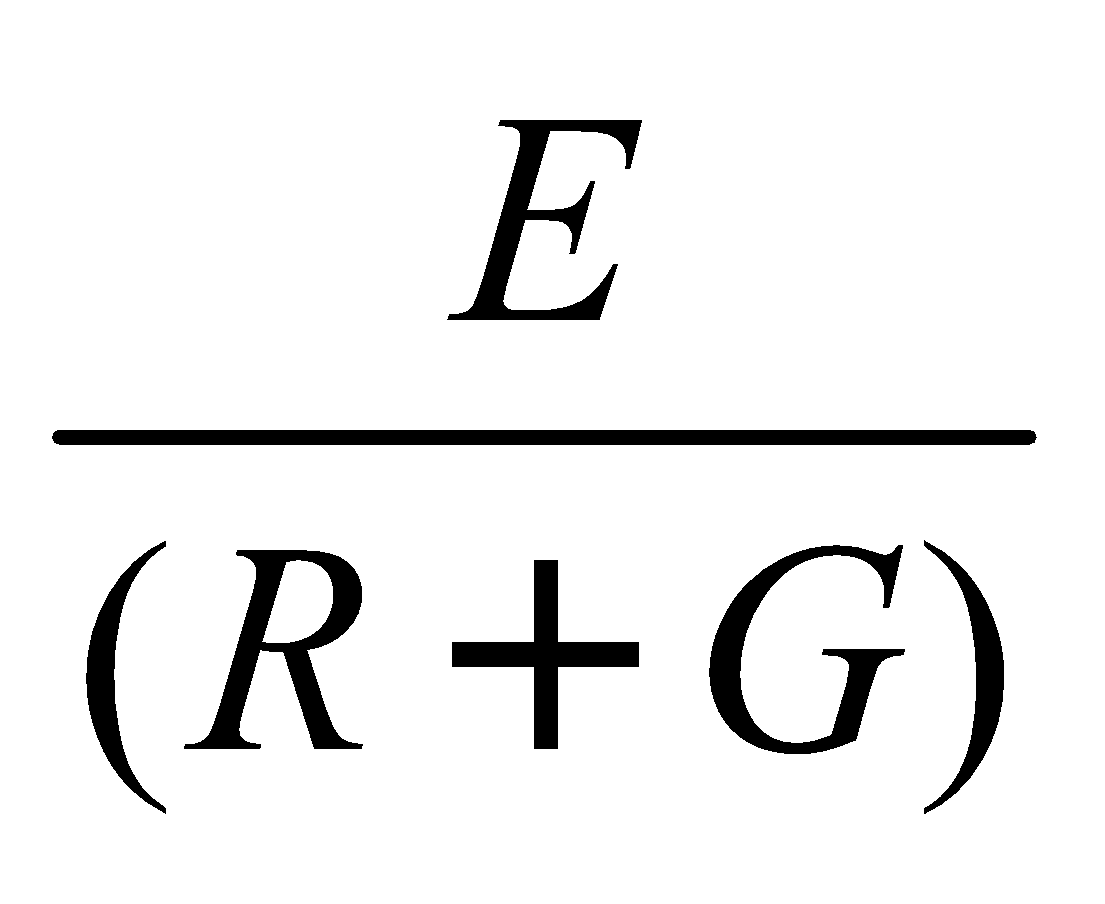
Where θ is the deflection of the galvanometer when current through it is Ig.
OBSERVATIONS
Resistance of galvanometer (G) :
Figure of merit (K) :
PRECAUTIONS
- The e.m.f. of cell or battery should be constant.
- The ammeter used for verification should preferably be of same range, as the range of conversion.
- Initially a high resistance from the resistance box should be introduced in the circuit (otherwise for small resistance an excess current will flow and damage the galvanometer or ammeter).
- Measure the diameter of the shunt resistance wire (neither too small nor too large in length) accurately.
EXPERIMENT 15(A)
AIM
To determine the focal length of a concave mirror.
MATERIAL REQUIRED
Concave mirror, object needle, metre scale etc.
THEORY
Let an object needle be at a distance 'u' from the mirror. Position of image is found by removing the parallax between the image of the object needle and the image needle.
Let 'v' be the distance of the image from the mirror. Then the focal length of the mirror 'f' is calculated from the relation 
1st method : (graphical)
A graph is plotted to represent u along X-axis and v-along Y axis. It is a rectangular hyperbola.
To calculate the focal length from the graph a line OP is drawn from the origin to a point P on the graph making an angle 45° with x-axis. Draw PM and PR perpendiculars on the axes. OM which gives the value of 2f from which f can be calculated.
2nd method : (graphical)
When a graph of 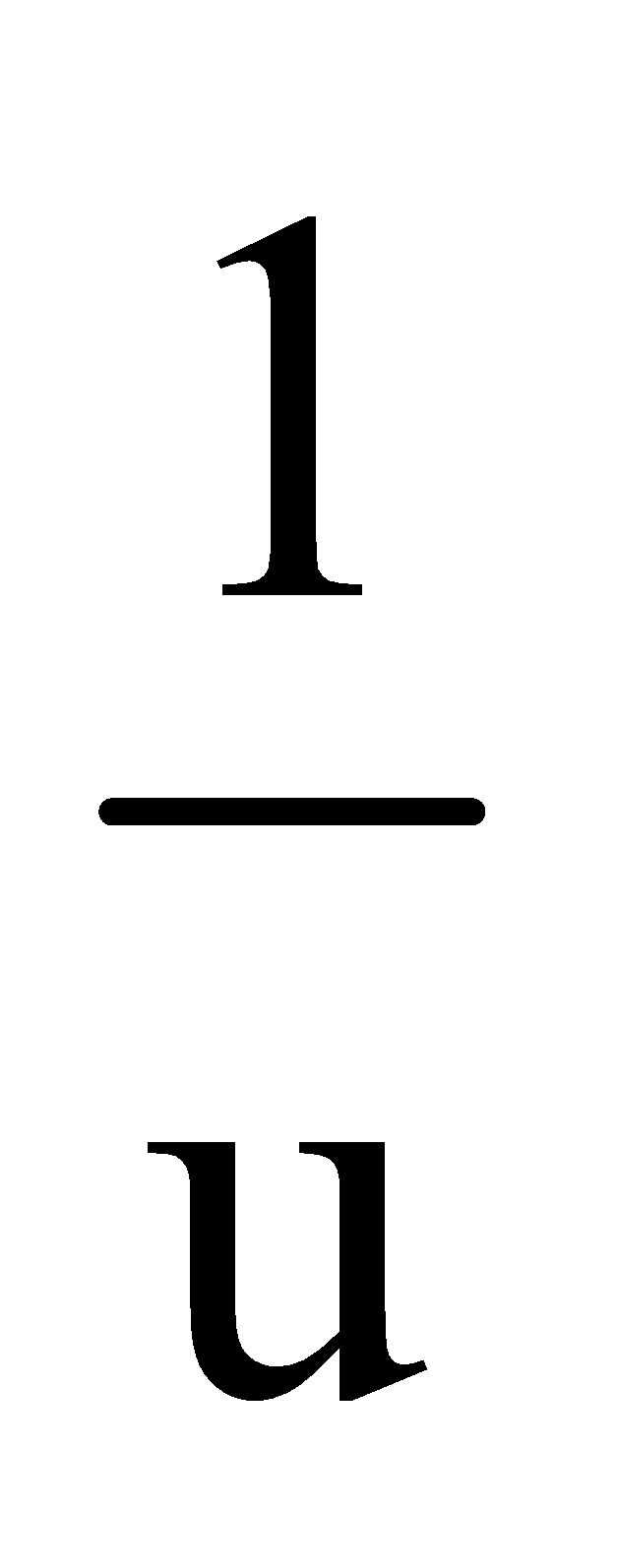 versus
versus 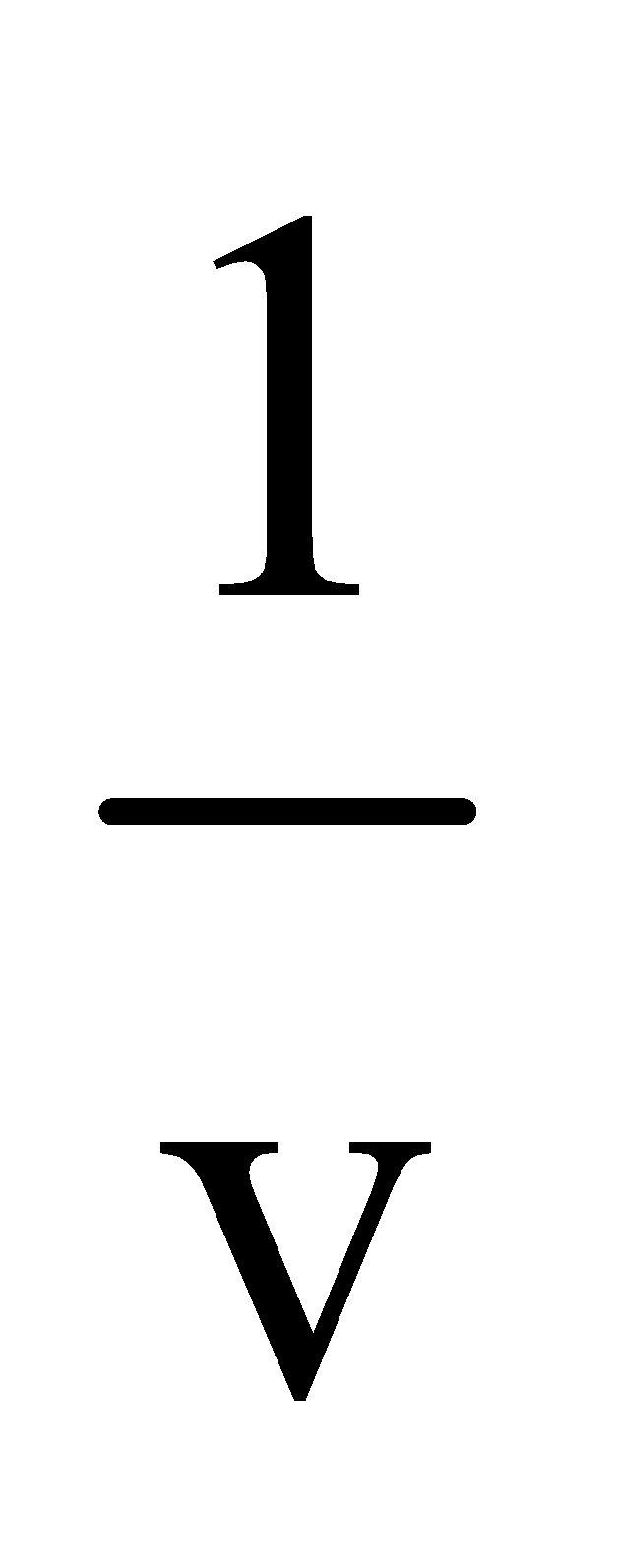 is plotted, it is a straight line.
is plotted, it is a straight line.
Select proper scale to represent 1/u along X-axis and  along Y-axis. The straight line will cut the axes at A and B at 45°.
along Y-axis. The straight line will cut the axes at A and B at 45°.
Then f = 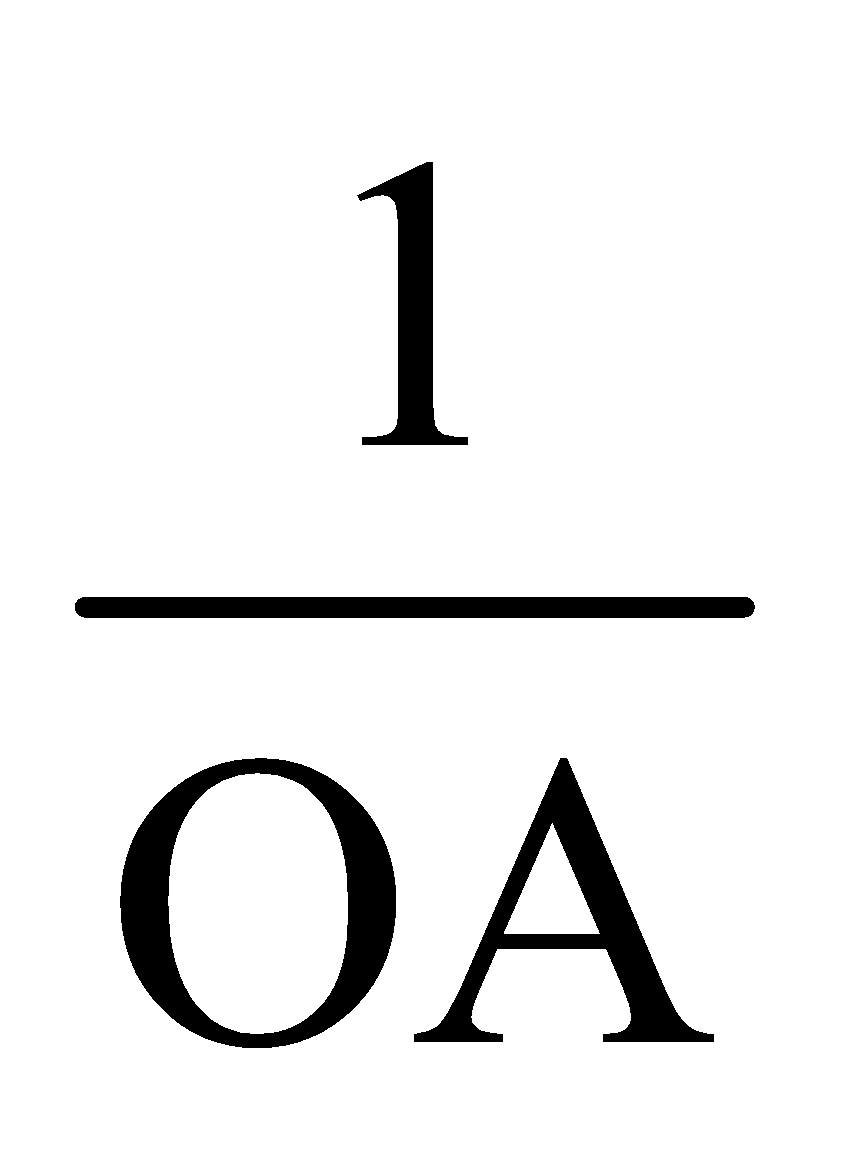 or
or 
OBSERVATIONS
EXPERIMENT 15(B)
AIM
To find the focal length of convex mirror using convex lens.
MATERIAL REQUIRED
Convex mirror, convex lens, metre scale.
THEORY
Focal length f = 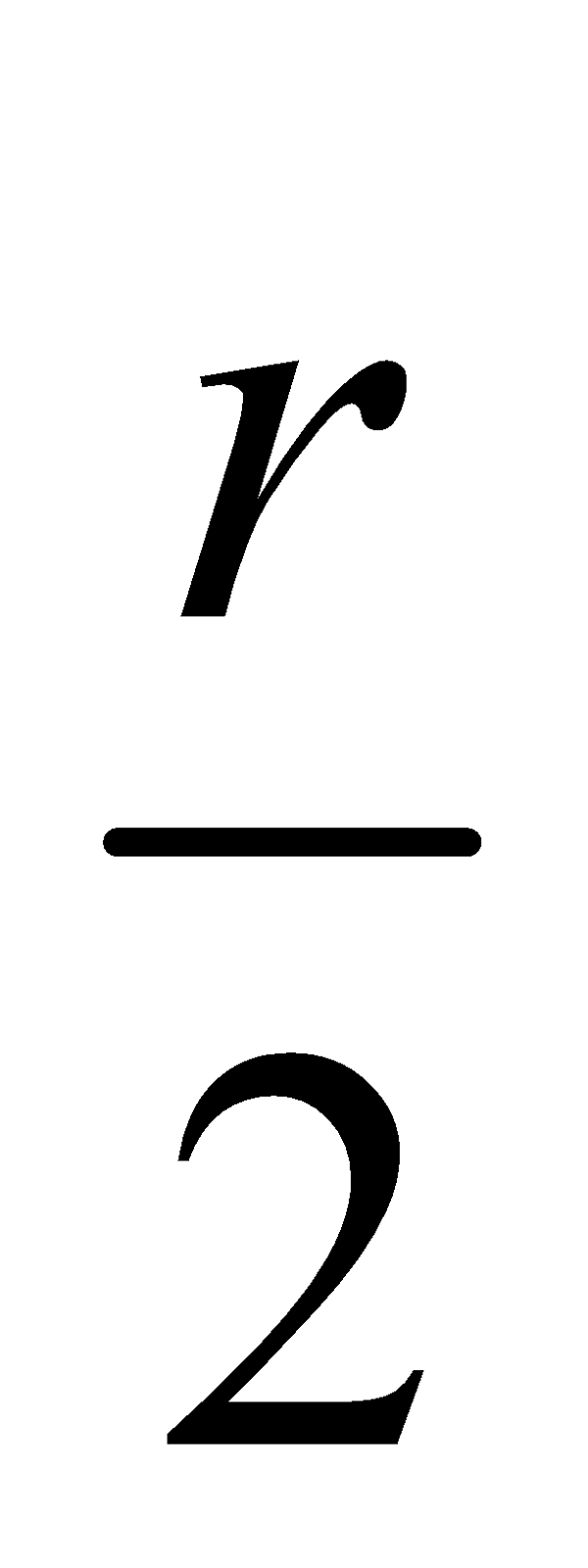 or, r = 2f
or, r = 2f
Descriptions
A convex mirror always forms a virtual image. So it is not possible to obtain it on the screen and hence measure image distance. So a convex lens is used to make the real image.
Let O be a point object on the axis of a convex lens L and I its real image. A convex mirror M is put between L and I and its position is so adjusted so that I is the centre of curvature of the mirror. The rays of light after refraction through the lens will then fall normally on it. They are reflected back along the original path and the real image (I2) formed in coincidence with O. Then PI is the radius of curvature (r) of the convex mirror.
OBSERVATIONS
Index error to be calculated.
EXPERIMENT 15(C)
AIM
To find the focal length of a convex lens by plotting u versus v graph and
and versus graph.
versus graph.
MATERIAL REQUIRED
Convex lens, image needle and metre scale.
THEORY
The focal length is calculated by the relation 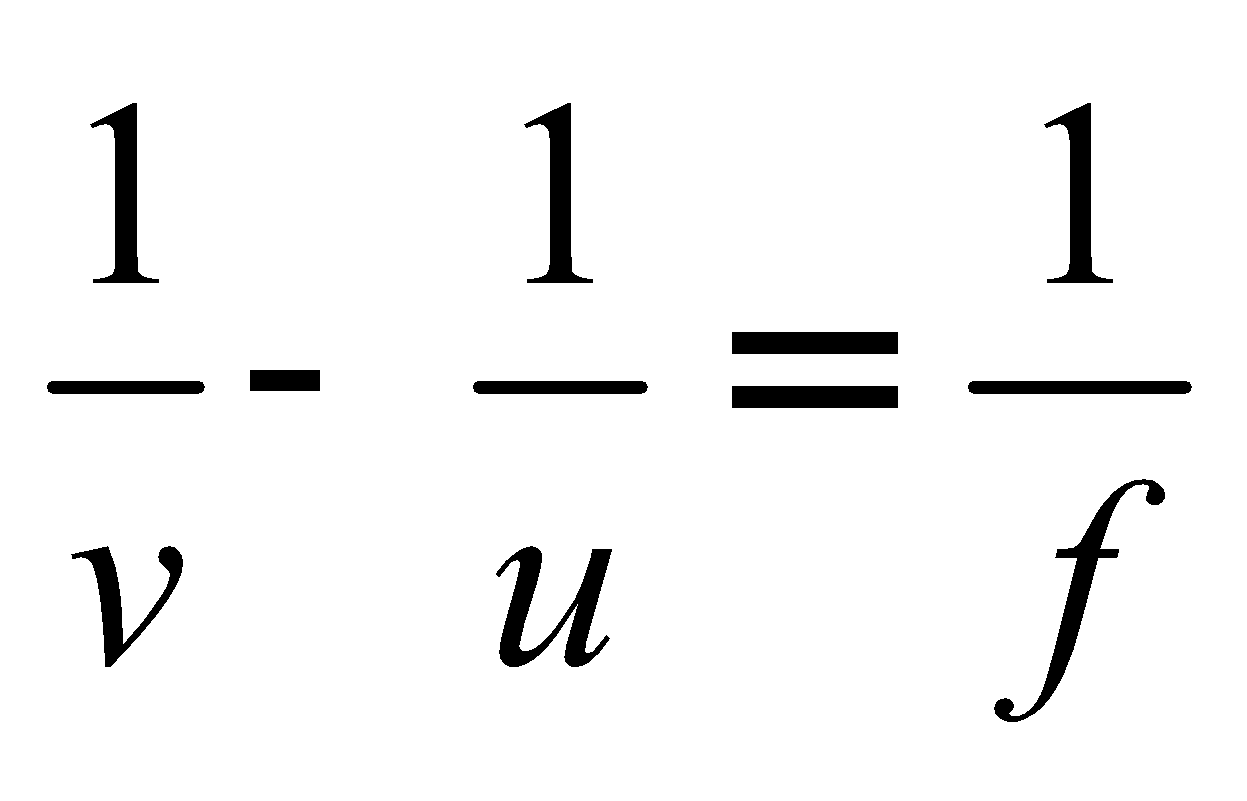
DESCRIPTION
When an object needle (AB) is placed in front of a convex lens at a distance greater than the focal length of the lens, its real, inverted image is formed on the other side. By placing a second needle there, the position of the image of the object needle can be located by removing the parallax between this image and the second needle itself.
Calculation of 'f ' from graphs:
1st method : u vs v graph
The graph is in the 2nd quadrant as u is negative by choosing a suitable scale u is plotted along X-axis and v along Y-axis. The graph will be a rectangular hyperbola. Draw a line (OP) making an angle of 45° with X-axis. From P draw perpendiculars PM and PN on X and Y axes respectively. OM = ON = 2f.
f = 
2nd method :  graph
graph
focal length = f =  or
or 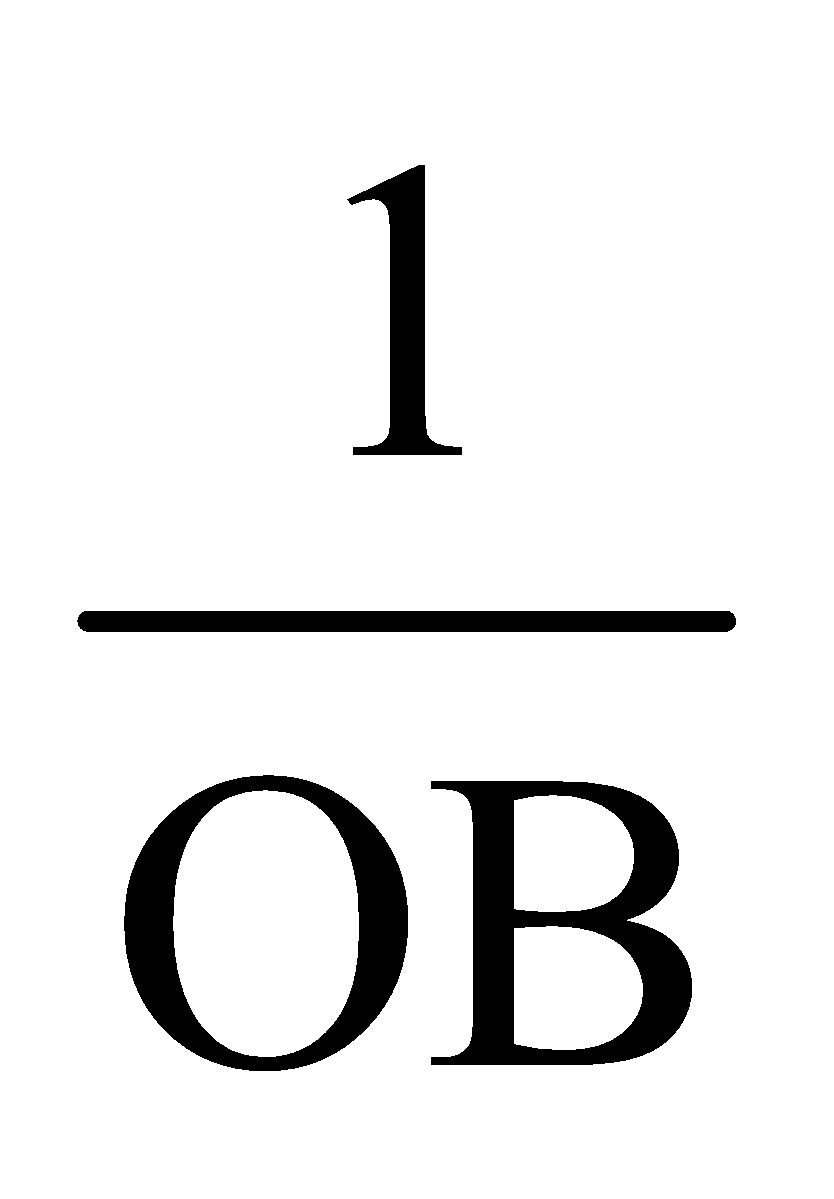 .
.
OBSERVATIONS
PRECAUTIONS
(FOR EXPERIMENT A AND B)
- Principal axis of the mirror should be horizontal and parallel to the central line of the optical bench.
- The uprights should be vertical.
- Tip to tip parallax should be removed between the needle and image of the needle.
- To locate the position of the image the eye should be at least 30 cm away from the needle.
- Tips of the object and image needles should lie at the same height as that of pole of the concave mirror.
- Index correction for u and v should be applied.
(FOR EXPERIMENT C)
- Tips of the object and image needles should lie at the same height as the centre of the lens.
- Parallax should be removed from tip to tip by keeping eye at a distance atleast 30 cm away from the needle.
- The object needle should be placed at such a distance that only real, inverted image of it is formed.
- Index correction for u and v should be applied.
EXPERIMENT 16
AIM
Using parallax method, to plot a graph of angle of deviation vs angle of incidence for a triangular prism.
MATERIAL REQUIRED
A prism, a protractor, drawing board, drawing pins.
THEORY
The refractive index of the material be calculated by the formula.
where,A = angle of prism, Dm = angle of minimum deviation
DESCRIPTION
If a graph is plotted between angle of incidence (i) along X-axis and angle of deviation (Dm) along Y-axis, then angle of deviation first decreases with increase in angle of incidence, becomes minimum (Dm) at a particular angle of incidence then increases again. The angle of minimum deviation is measured from the graph. Angle of prism (A) for an equilateral prism is 60°.
The angle of deviation is calculated for various angle of incidences by parallax method. Two pins P1 and P2 [refer to fig. (1)] are put on the incident ray and their images are seen through the other face of the prism. Two pins P3 and P4 are put on the same line as the images of P1 and P2.
OBSERVATIONS
PRECAUTIONS
- A sharp pointed pencil should be used for drawing boundary of the prism and for making the pin pricks.
- The angle of incidence should lie between 30º–60º.
- The pins should be fixed vertical.
- The distance between the two pins should not be less than 10 cm.
- Arrow heads should be marked to represent the incident and emergent rays.
- The same angle of prism should be used for all the observations.
EXPERIMENT 17
AIM
To determine the refractive index of a glass slab using a travelling microscope.
MATERIAL REQUIRED
Travelling microscope, ink, white paper and glass slab.
THEORY
Refractive index of glass μ = 
DESCRIPTION
Put an ink mark on a paper. Focus the microscope to note the mark. The position of the microscope is noted from the scale. Put the glass slab on the mark. Raise the microscope to focus the image of the mark again. Note this position from the scale. Now put another mark on the top surface of the glass slab and focus it again.
OBSERVATIONS
PRECAUTIONS
- In microscope, the parallax should be properly removed.
- The microscope should be moved in upper direction only to avoid backlash error.
EXPERIMENT 18
AIM
To draw the characteristic curves of a p-n junction diode in forward and reverse bias.
MATERIAL REQUIRED
PN junction diode, milliammeter, micro-ammeter, voltmeter, potentiometer and battery.
THEORY
Forward-bias Pn junction
It produces forward current. With increase in bias voltage the forward current increases slowly in the beginning and then rapidly. At about 2.4 V, the current increases suddenly. The bias is at once made zero to avoid damage to the diode.
Reverse-bias Pn junction
In the beginning no appreciable reverse current flows. At about 5V a feeble current starts flowing. With increase in bias voltage, the current slowly increases. At about 25 V the reverse current increases suddenly. Again the bias is made zero to avoid damage.
DESCRIPTION
When the p-side is connected to positive and n-side to negative of a cell the diode is forward biased. When the p-side is connected to negative and n-side to positive of a cell the diode is reverse biased. If the voltage is plotted along X-axis and current along y-axis then it is called a V–I characteristic curve.
In the forward region, the voltage where the current start to increase rapidly is called knee voltage.
The dynamic or a.c. resistance can be calculated from the slope of the curve. ra.c = 
The forward resistance of the diode is low. The resistance decreases with increase in current. The reverse resistance is very high at the beginning but decreases beyond breakdown voltage.
OBSERVATIONS
PRECAUTIONS
- All connections should be neat, clean and tight.
- Key should be used in circuit and opened when the circuit is not being used.
- Forward-bias voltage beyond breakdown should not be applied.
- Reverse-bias voltage beyond breakdown should not be applied.
EXPERIMENT 19
AIM
To draw the characteristic curves of a Zener diode and finding reverse breakdown voltage.
MATERIAL REQUIRED
Zener diode, battery micro ammeter and voltmeter.
THEORY
Zener diode a semiconductor diode, in which the n-type and the p-type sections are heavily doped, i.e., they have more percentage of impurity atoms. This heavy doping results in a low value of reverse breakdown voltage (BVR). This value can be controlled during manufacture.
The reverse breakdown voltage of Zener diode, is called Zener current (IZ).
Circuit Parameters : In the circuit given before (Fig. 10.08)
VI = Input (reverse bias) voltage
VO = Output voltage (RL/IL)
RI = Input resistance
RL = Load resistance
IL = Input current (reverse current)
IZ = Zener diode current
IL = Load current
Relations :
IL = II – IZ .......... (1)
VO = VI –RI II .......... (2)
VO = RLIL .......... (3)
Initially as VI is increased, II increases a little, then VO increases.
At break-down, increase of VI increases II by large amount, so that VO = VI – RIII becomes constant.
This constant value of VO which is the reverse breakdown voltage, is called Zener voltage.
Formula used : VO = VI – RIII
Constant value of VO gives reverse breakdown voltage.
DESCRIPTION
Zener diode normally operates under reverse bias condition so the output voltage remains constant even if input voltage and hence the current changes. From the reverse bias characteristics the breakdown voltage is calculated. It is the voltage at which the reverse current start increasing enormously.
OBSERVATIONS
From the graph, reverse breakdown voltage = ________ volt.
PRECAUTIONS
- All connection should be neat, clean and tight.
- Key should be used in circuit and opened when the circuit is not being used.
EXPERIMENT 20
AIM
To draw the characteristic curves of a transistor and finding current gain and voltage gain.
MATERIAL REQUIRED
Transistor, milliammeter microammeter, voltmeter, potentiometer, rheostat and battery.
CHARACTERISTIC CURVES
Input characteristics : Here input current is plotted against input voltage. For common emitter configuration the input voltage is emitter to base voltage and input current is base current. Here output voltage is kept constant. From the slope of input characteristics input resistance is calculated.
Input resistance = Ri = 
Output characteristics : Here output voltage is plotted against output current. For common emitter configuration, the output voltage is collector to emitter voltage (VCE) and output current is collector current (IC). Here input current is kept constant. From the slope of output characteristics output resistance (RO) is calculated.
Output resistance = RO = 
Transfer characteristics : If a graph is plotted with base current (Ib) along X-axis and output current (Ic) along Y-axis then it is called transfer characteristics. Here output voltage is kept constant.
From the slope of transfer characteristics current gain is calculated.
Current gain =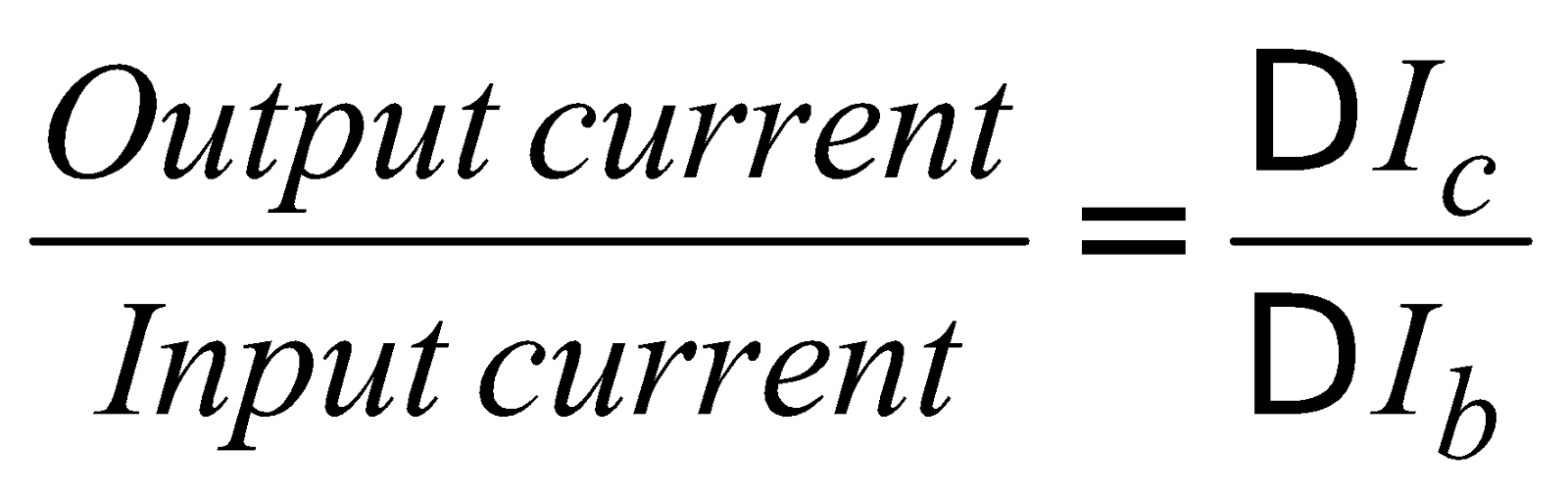 ;
;
Resistance gain = 
∴ Voltage gain = current gain × resistance gain
OBSERVATIONS
Output characteristics : Transfer characteristics :
Base current = Ib μA Collector voltage = VC V
PRECAUTIONS
- All connections should be neat, clean and tight.
- Key should be used in circuit and opened when the circuit is not being used.
- Forward-bias voltage beyond breakdown should not be applied.
- Reverse-bias voltage beyond breakdown should not be applied.
EXPERIMENT 21
AIM
To identify diode, LED, transistor, IC, resistor, capacitor from mixed collection of such items.
DESCRIPTION
- Diode : Diodes are two terminal devices. A diode is a device that has a very high resistance when connected in reverse bias i.e. the p-side is connected to negative side of the battery and n-side to positive of the battery. But it has a very low resistance when connected in forward bias i.e. p-side is connected to positive and n-side to negative of a battery.
Semiconductor diodes are designed by two letters followed by a serial number. The first letter indicates the material : A is used for material with a band gap of 0.6 eV to 1.0 eV such as germanium. B is used for material with a band gap of 1.0 eV to 1.3 eV, such as silicon. The second letter indicates the main application : A signifies detection diode. B denotes a variable capacitance diode, E. for tunnel diode, Y for rectifying diode and Z denotes zener diode. The serial number specify the diodes with particular values of power rating, peak reverse voltage, maximum current rating etc. For example, BY127 and BZ148 respectively denote a silicon rectifier diode and a silicon zener diode.
To make visual identification of anode and cathode, the diode manufactures employ one of the following ways :
- The symbol is painted on the body of the diode.
- Red and blue marks are used on the body of the diode. Red mark denotes anode, whereas blue indicates the cathode.
- A small ring is printed at one end of the body of the diode that corresponds to the cathode.
- LED (light emitting diode) : It is a p-n junction diode, operates in forward bias and emits light. It's negative leg is longer than the positive.
(a) A typical LED
(b) Structure of LED
- Transistor : It is a three legged device. They are emitter, base and collector. There is connection between emitter, base and base, collector. So any component that has three legs in a given mixed collection of item is a transistor.
- IC (Integrated circuit) : It is a device in which many thousands of transistors is packed on a slice of semiconductor. It is protected by a small plastic case and all the connections are brought out to metal legs on each side of IC. Therefore, the component having more than 3 legs is an IC.
External view of an IC
- Resistor : They are 2 terminal devices. When it is connected in a d.c. circuit, it shows a constant current. It shows continuity both in direct and reverse connectors.
- Capacitor : Capacitors are two terminal devices. When it is connected to a battery, electric charge immediately flows into the capacitor until it is full. This takes fraction of a second. With a multimeter it shows a full scale deflection indicating small resistance initially which becomes infinite in a fraction of a second.
Capacitors
EXPERIMENT 22
Using multimeter to
- identify base of a transistor
- distinguish between n-p-n and p-n-p type of transistor.
- see the unidirectional flow of current in case of a diode and a LED.
- check the correctness or otherwise of a given electronic component (diode, transistor or IC)
DESCRIPTION
A multimeter or a multitester, also known as a volt/ohm meter or VOM, is an electronic measuring instrument that combines several function in one unit. A standard multimeter may include features such as the ability to measure voltage, current and resistance. There are two categories of multimeters, analog multimeters and digital multimeters (often abbreviated as DMM)
A multimeter can be a hand-held device useful for basic fault finding and field service work or a bench instrument which can measure to a very high degrees of accuracy. They can be used to troubleshoot electrical problems in a wide array of industrial and household devices such as batteries, motor controls, appliances, power supplies, and wiring systems.
Analog multimeter
Digital multimeter
- A transistor is either p-n-p or n-p-n having three connections emitter, base and collector. If a multimeter is connected between emitter and base and then between base and collector conduction takes place in both cases, then the lead of the multimeter which is common in both cases is called base.
PROCEDURE
If a multimeter with a "diode check" function is used in to test transistor, it will be found that the emitter-base junction has a slightly greater forward voltage drop than the collector-base junction. This forward voltage difference is due to imbalance in doping concentration between the emitter and collector regions of the transistor. The emitter region is heavily doped compared to collector region, causing its junction with the base to produce a higher forward voltage drop.
- meter touching wire a (+) and b(–) : "OL" (no reading)
- meter touching wire a (–) and b(+) : "OL" (no reading)
- meter touching wire a (+) and c (–) : 0.65 volt
- meter touching wire a (–) and c (+) : "OL" (no reading)
- meter touching wire b (+) and c (–) : 0.63 volt
- meter touching wire b (–) and c (+) : "OL" (no reading)
The only combinations of test points giving conducting meter readings are wires a and c (red test lead on a and black test lead on c), and wires b and c (red test lead on b and black test lead on c). These two readings must indicate forward biasing of the emitter-to-base junction (0.65 volts) and the collector-to-base junction (0.63 volts).
Now we look for the one wire common to both sets of conductive readings. It must be base connection of the transistor, because the base is the only layer of the three-layer device common to both sets of PN junctions (emitter-base and collector-base).
In this example, that wire is number c, being common to both the a-c and the b-c test point combinations. In both those sets of meter readings, the black (–) meter test lead was touching wire c, which tells us that the base of this transistor is made of N-type semiconductor material (black = negative). Thus, the transistor is an PNP type with base on wire c, emitter on wire a and collector on wire b.
SUMMARY
Use a multimeter, battery, resistor and LED to check each pair of leads for conduction. Set digital multimeter at diode test point and an analogue multimeter at low resistance range.
Test each pair of leads both ways (therefore total tests = six) :
- The base-emitter (BE) junction should conduct like a diode and current is made to flow in one direction only.
- The base-collector (BC) junction should behave like a diode and conduct in one direction only.
- The collector-emitter (CE) should not conduct either way.
The above diagram shows how the junctions behave in a NPN transistor. In case of a PNP transistor same test procedure can be used.
- For conduction to be possible in both the cases mentioned above, if the common terminal (i.e. black lead of multimeter) is connected to base then the transistor is p-n-p type. If the positive terminal (red lead) of the multimeter is connected to base then the transistor is n-p-n type.
Identification of N-P-N and P-N-P transistor : With the help of multimeter we can identify P-N-P and N-P-N transistor. In this process, by putting multimeter in 1Q range, we measure resistance between emitter-base and base-collector. We connect Black probe of multimeter to transistor’s base and connect red prob to emitter and collector respectively, if needle of meter shows low resistance (i.e. gives large indication) then transistor is N-P-N transistor. When we connect red prob to base and connect black prob to emitter and collector respectively and if meter shows low resistance (means large indication) then transistor will be P-N-P transistor. Each transistor will be either P-N-P type or N-P-N type. So meter shows low resistance only for one checking.
- If the positive of the multimeter is connected to p-side and negative to n-side of a p-n junction diode or a LED then a continuous current flow is obtained but for reverse connection it stops.
Connect the multimeter in series with the circuit connecting the red test lead towards positive side and black test lead towards the negative side. Now, turn on the power in the circuit and observe the deflection of the pointer. Vary the output of the battery eliminator and read the value of the current. Since the diode is forward biased allow the current to pass.
Now reverse the terminals of the diode and again observe the current on the appropriate scale of the multimeter. Since the multimeter shows no current reading on the scale, this means the junction diode does not allow the current to pass through it. In other words the junction diode allows the passage of current in one direction only i.e., the current in the junction diode is unidirectional.
Now replace the junction diode by the LED. And repeat the steps of the procedure mentioned above in the case of junction diode. It will be observed that the current in a LED is also uni directional i.e., it allows the flow of current when it is forward biased and it emits red, yellow and green light. No light is emitted on reversed bias which, if it exceeds by 5 V may damage the LED.
- To check the correctness of a component like diode or transistor it has to be connected with the multimeter in such a way that the continuity of the current is observed.
Diode test with an analog multimeter
- Set the meter to its ohms range - any range should do, but the middle ohms range if several are available is probably best.
- Connect the cathode terminal of the diode to the terminal marked positive on the multimeter, and the anode to the negative or common terminal.
- Set the meter to read ohms, and a “lowish” reading should be obtained.
- Reverse the connections.
- This time a high resistance reading should be obtained.
Transistor test using an analog multimeter
The instructions are given primarily for an NPN transistor as these are the most common types in use. The variations are shown for PNP varieties.
- Set the meter to its ohms range - any range should do, but the middle ohms range if several are available is probably best.
- Connect the base terminal of the transistor to the terminal marked positive (usually coloured red) on the multimeter
- Connect the terminal marked negative or common (usually coloured black) to the collector and measure the resistance. It should read open circuit (there should be a deflection for a PNP transistor).
- With the terminal marked negative still connected to the base, repeat the measurement with the positive terminal connected to the emitter. The reading should again read open circuit (the multimeter should deflect for a PNP transistor).
- Now reverse the connection to the base of the transistor, this time connecting the negative or common (black) terminal of the analog test meter to the base of the transistor.
- Connect the terminal marked positive, first to the collector and measure the resistance. Then take it to the emitter. In both cases the meter should deflect (indicate open circuit for a PNP transistor).
- It is next necessary to connect the meter negative or common to the collector and meter positive to the emitter. Check that the meter reads open circuit. (The meter should read open circuit for both NPN and PNP types).
- Now reverse the connections so that the negative of meter or common is connected to the emitter and positive of meter to the collector. Check again that the meter reads open circuit. If the transistor passes all the tests then it is basically functional and all the junctions are intact.










