RAY OPTICS AND OPTICAL INSTRUMENTS
REFLECTION OF LIGHT
It is the turning back of light in the same medium.
LAWS OF REFLECTION
- Angle of incidence (i) = angle of reflection (r)
- The incident ray, reflected ray and normal are always in same plane.
REFLECTION FROM PLANE SURFACE
Plane mirror has infinitely large radius of curvature. It produces virtual image of same size but laterally inverted. Image is as much behind the mirror as much is the object in front of it.
- If the direction of the incident ray is kept constant and the mirror is rotated through an angle θ about an axis in the plane mirror, then the reflected ray rotates through an
angle 2θ.
- If an object moves towards (or away from) a plane mirror at a speed v, the image will also approach (or recede) at the same speed v, i.e. the speed of image relative to object will be v – (–v) = 2v.
- If two plane mirrors are inclined to each other at 90º, the emergent ray is always antiparallel to incident ray if it suffers one reflection from each whatever be the angle of incidence. The same is found to hold good for three-plane mirrors forming the corner of a cube if the incident light suffers one reflection from each of them.
- If there are two plane mirrors inclined to each other at an angle θ, the no. of images of a point object formed are determined as follows :
- If
is even integer (say m), no. of images formed
n = (m – 1), for all positions of object. - If
is odd integer (say m), no. of images formed,
n = m, if the object is not on the bisector of mirrors
n = (m – 1), if the object is on the bisector of mirrors. - If
is a fraction, the no. of images formed will be equal to its integral part.
Note:- A plane mirror always forms a virtual image if object is real and forms a real image if the object is virtual.
MIRROR FORMULA
where, u = distance of the object from the pole of mirror
v = distance of the image from the pole of mirror
f = focal length of the mirror.
Mirror formula is valid only when the following conditions are satisfied :
- Object is placed very near to the principal axis.
- Object is placed far from the mirror.
MAGNIFICATION
where, I = size of the image and O = size of the object and negative sign implies that image is inverted w.r.t the object.
The above formulae are applicable only for paraxial rays (the rays which makes very small angle with the principal axis).
Areal magnification : When a two dimensional object is placed with its plane perpendicular to the principal axis, its magnification called superficial magnification or aerial magnification and is given by
SIGN CONVENTIONS FOR MIRROR AND LENSES
New Cartesian sign conventions :
- All the distances are measured from pole of spherical mirror and optical centre in case of lenses.
- The distances measured in a direction opposite to the direction of incident light is taken as negative and vice-versa.
- The heights measured upward and perpendicular to the principal axis of mirror are taken as positive and vice -versa.
- Angle measured from the normal in the anticlockwise direction is positive and vice-versa.
IMAGE FORMED BY CONCAVE AND CONVEX MIRROR
IMAGE FORMED BY CONCAVE MIRROR
IMAGE FORMED BY CONVEX MIRROR
KEEP IN MEMORY
- Rays retrace their path when their direction is reversed.
- Focal length of a mirror depends only on the curvature of the mirror
.
It does not depend on the material of the mirror or on the wavelength of incident light. - Focal length of concave mirror is always negative.
Focal length of convex mirror is always positive.
- The graph of
versus
for a concave mirror, if real image is formed.
- The graph shows variation of v with change in u for a mirror.
- A person needs a plane mirror of minimum half of his height to see his full image.
- A person standing in the middle of room can see complete wall behind him if the mirror in front of him is
rd of height of wall.
- A convex mirror is used as a rear view mirror (called driver mirror).
- If two or more optical components produce magnification, then overall magnification (m) is the product of magnification due to each component,
i.e., m = m1 × m2× . . .
If m is negative, the image is inverted
If m is positive, the image is erect.
- When an object moves with constant speed towards a concave mirror from infinity to focus, the image will move away from the mirror slower in the beginning and with the speed of the object when it is at centre of curvature C and faster later on.
- Concave mirrors are used as reflectors, as objective in reflecting telescope and by doctors (ENT) to examine ears, nose and throat. It is also used as shaving mirrors.
- The inability of a spherical mirror (or lens) of large aperture to focus the paraxial rays and marginal rays to the same point on the principal axis is called spherical aberration. Due to this defect the image formed is blurred. This defect can be removed by using parabolic mirror.
- Chromatic aberration is absent in mirrors but present in lenses. This is because the focal length of mirror is independent of wavelength of light
but that of lens is dependent on wavelength.
- Different colour rays travel with different velocity in a medium but velocity of all coloured rays is same in vacuum (and air).
- If a hole is formed in a mirror, then also we will get full image with no hole in the image. The hole will only reduce the intensity of rays forming the image.
NEWTON’S FORMULA
In case of spherical mirrors if object distance (x1) and image distance (x2) are measured from focus instead of pole, u = (f + x1) and v = (f + x2),
the mirror formula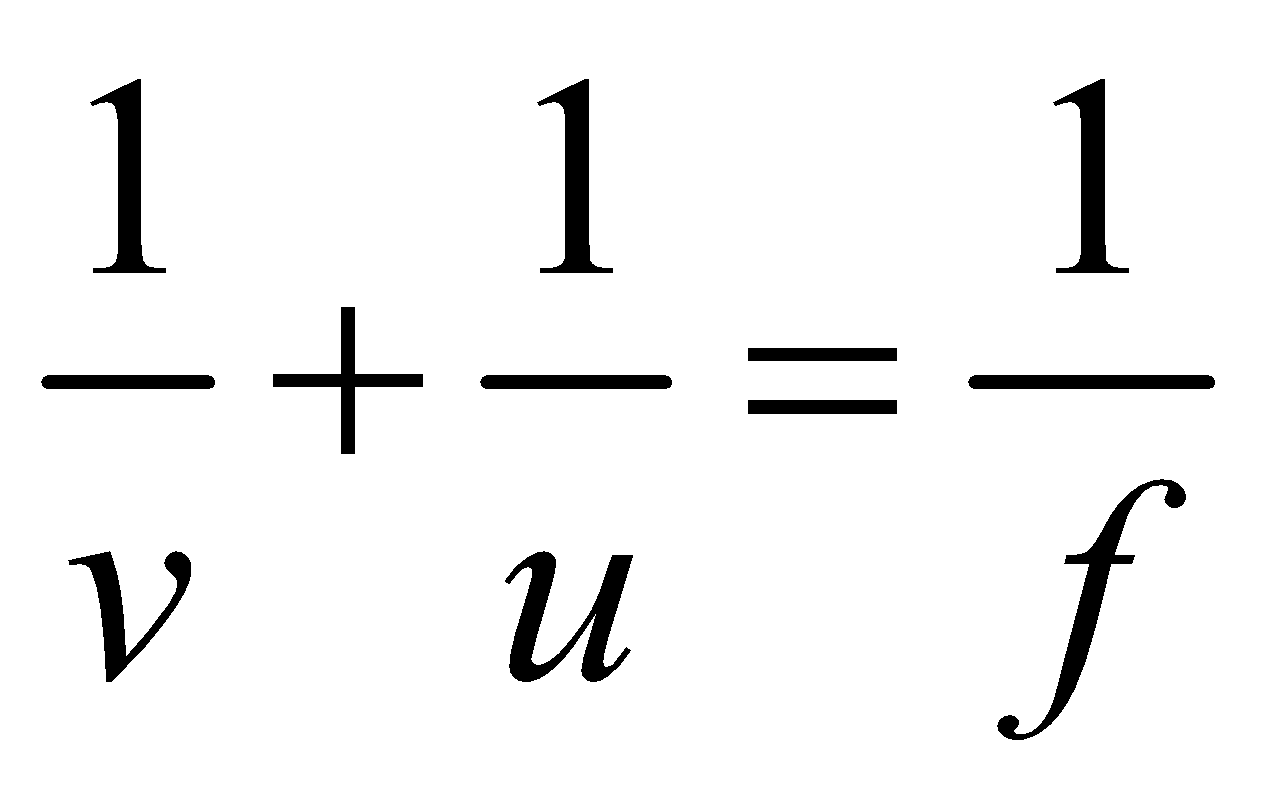
the mirror formula
reduces to 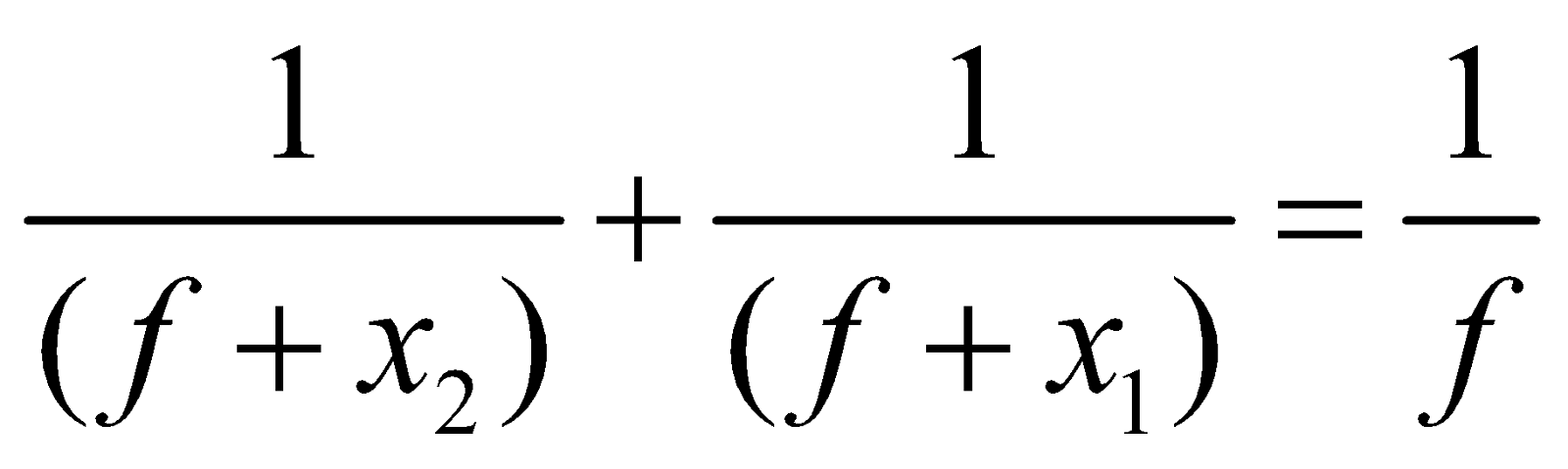
which on simplification gives x1 x2 = f2
REFRACTION
Whenever a wave is bounced back into same medium at an interface reflection is said to have occurred. Transmission of a wave into the second medium at an interface is called refraction. When a ray of light is passing from denser to rarer medium, it bends away from the normal and when passing from rarer to denser medium, it bends towards the normal.
- When a ray of light passing from one medium to another medium frequency and phase do not change while wavelength and velocity changes.
- Twinkling of stars, appearance of sun before actual sunrise and after actual sunset etc. are due to atmospheric refraction.
LAWS OF REFRACTION
- Snell's Law : When a light ray is incident on a surface separating two transparent media, the ray bends at the time of changing the medium.
i.e.  ,
,
where i = angle of incidence
r = angle of refraction
v1 = vel. of light in 1st medium
v2 = vel. of light in 2nd medium
μ1 = refractive index of 1st medium w.r.t vacuum (or air)
μ2 = refractive index of 2nd medium w.r.t vacuum (or air)
- The incident ray, the normal and the refracted ray at the interface all lie in the same plane.
REFRACTIVE INDEX OF THE MEDIUM
REFRACTIVE INDEX OF SECOND MEDIUM W.R.T. FIRST MEDIUM
ABSOLUTE REFRACTIVE INDEX OF MEDIUM (n OR µ)
Refractive index is the relative property of two media. If the first medium carrying the incident ray is a vacuum, then the ratio  is called the 'absolute refractive index of the second medium'. The relative refractive index of any two media is equal to the ratio of their absolute refractive indices.
is called the 'absolute refractive index of the second medium'. The relative refractive index of any two media is equal to the ratio of their absolute refractive indices.
Therefore, if the absolute refractive index of medium 1 and 2 be n1 and n2 respectively, then the refractive index of medium 2 with respect to medium 1 is
n1 sin i = n2 sin r
According to cauchy’s formula
where, A and B are cauchy’s constant.
λred > λviolet so, μred < μviolet
- For three mediums 1, 2 and 3 due to successive refraction.
1n2 × 2n3 × 3n1 = 1
- For two mediums, n1 and n2 are refractive indices with respect to vacuum, the incident and emergent rays are parallel then
n1 sinφ1 = n2 sinφ2.
FACTORS AFFECTING REFRACTIVE INDEX
- Nature of the medium
- Wavelength
- Temperature of the medium-with increase in temperature, refractive index of medium decreases.
TRANSMISSION OF WAVE
- The equation of the wave refracted or transmitted to the next medium is given by : y = A´´ sin
. This is independent of the nature (rarer/denser) of the medium. The wave is not inverted.
- The amplitude (A´´) of the transmitted wave is less than that (A) of the incident wave.
- The angular frequency remains unchanged. However the wave number changes. Note that the phase of the transmitted wave is
and that of the incident wave is (ωt – kx).
- The compression or rarefaction are transmitted as such and same is the case with the crest or trough.
The wave velocity (vp), the angular frequency (ω) and the wave number (k) are related as vp = ω/k = nλ. Let the wave velocity in the medium to which the wave is transmitted be v'p = ω/k´ = nλ'.
- If second medium is denser, in comparison to first medium (i.e. μ2 > μ1), then from Snell’s law
⇒ k1 < k2 and λ1 > λ2.
It means that if ray goes from rarer medium to denser medium (i.e. from first medium to second medium), then wavenumber increases & wavelength decreases.
- If second medium is rarer in comparison to first medium, then from Snell’s law
⇒ k1 > k2 and λ1 < λ2.
It means that when ray goes from denser to rarer medium, then wave number decreases & wavelength increases.
- No change in wave number k occurs on reflection.
IMAGE DUE TO REFRACTION AT A PLANE SURFACE, APPARENT SHIFT
- Here O = position of object, I = position of image
- The image shifts closer to eye by an amount
OI = AO – AI or
where t = thickness of medium over the object
Δt = apparent shift in its position towards the observer.
When an object in denser medium is seen through rarer medium, then apparent depth is less than real depth. But when an aeroplane or bird flying is seen by an observers in denser medium, the apparent height is more by (μ – 1)t
Lateral shift by a slab of uniform thickness t, is

The apparent shift through a glass slab is in the direction of light
TOTAL INTERNAL REFLECTION (TIR)
When the object is placed in an optically denser medium and if the incident angle is greater than the critical angle then the ray of light gets reflected back to the originating medium. This phenomenon is called total internal reflection.
Critical angle (ic) : When a ray passes from an optically denser medium to an optically rarer medium, the angle of refraction r is greater than the corresponding angle of incidence i. From Snell’s law
Let μ1 = μ and μ2 = 1 and let for i = ic, r = 90º then 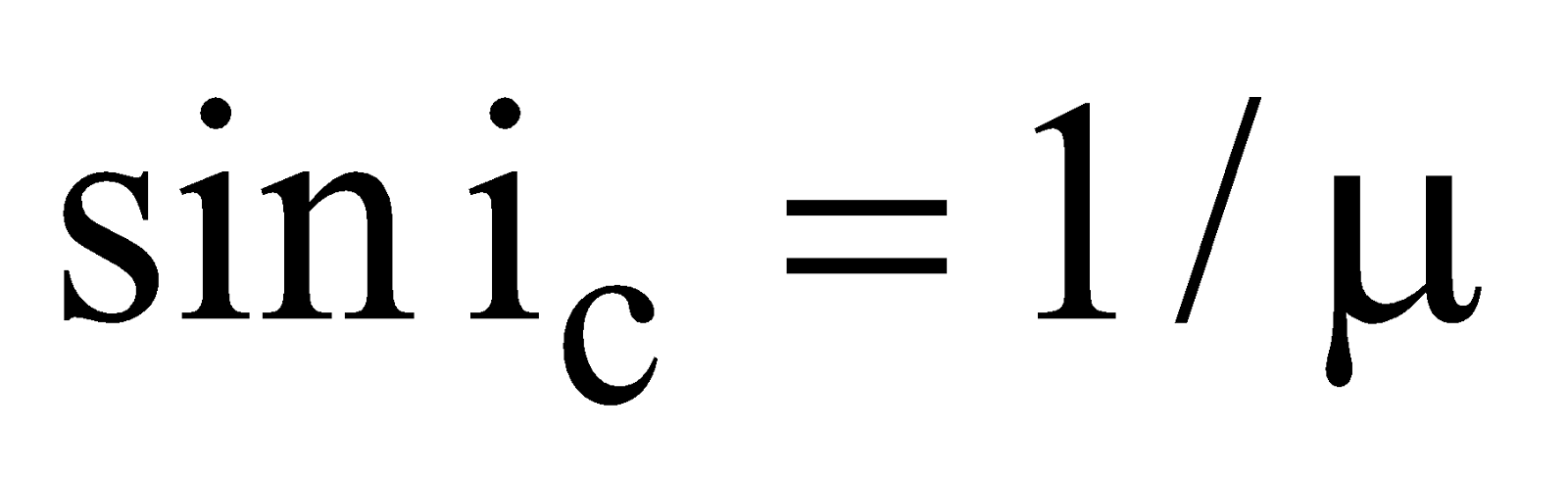
This phenomenon takes place in shining of air bubble, sparkling of diamond, mirage and looming, in optical communication using optical fibre.
KEEP IN MEMORY
- On travelling through a series of parallel layers, light follows the following formula
It is important to note that the above relationship is valid only when boundaries undeviated.
- In case of refraction, if i = 0 then r = 0. This means that the ray which strikes to a boundary at 90° passes through the boundary undeviated.
- If an object moves towards a denser medium with a velocity v then the image moves faster with speed of as seen by the observer in denser medium.
- If an object moves towards a rarer medium with a velocity v then the image moves slower with a speed v/μ as seen by the observer in rarer medium.
- Denser the medium, smaller is the wavelength.
- When light travels from one medium to another the wavelength and velocity changes proportionally but frequency of rays remains the same
and
(‘a’ for air/vacuum)
- When a parallel compound slab consists of two media of equal thickness and refractive indices and then the equivalent refractive index
COMMON DEFAULT
🗶 Incorrect : If a mirror or a lens is painted black on one half, then half of image will be formed.
✔ Correct : If half of the mirror or lens is blackened, we get full image but with half the intensity.
REFRACTION AT A SPHERICAL SURFACE
For any curved spherical surfaces. Relation between u and v in terms of refractive indices of the mediums and the radius of curvature of the curved spherical surface.
Spherical surface separating two media
LATERAL MAGNIFICATION in case of refraction from curved surfaces
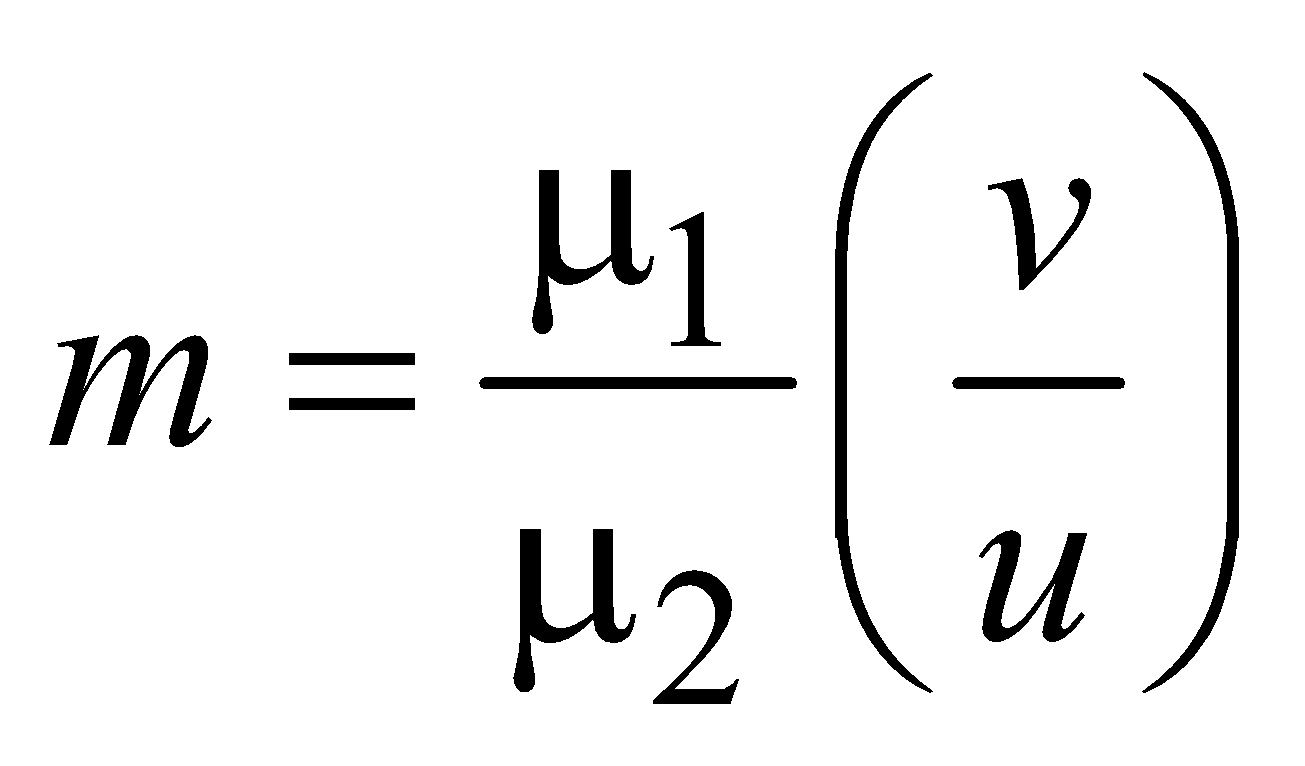
LONGITUDINAL MAGNIFICATION

Note:- μ1 is refractive index of medium 1 through which light passes first before meeting the interface and μ2 is the refractive index of medium 2 to which light encounters after it passes through the interface.
REFRACTION BY A LENS
The focus point of a lens is the point where image of an object placed at infinity is formed. And its distance from optical centre of the lens is called focal length.
Focal length of convex lens is +ve, and of concave lens is –ve.
LENS FORMULA OR THIN LENS FORMULA
LENS MAKER'S FORMULA
where 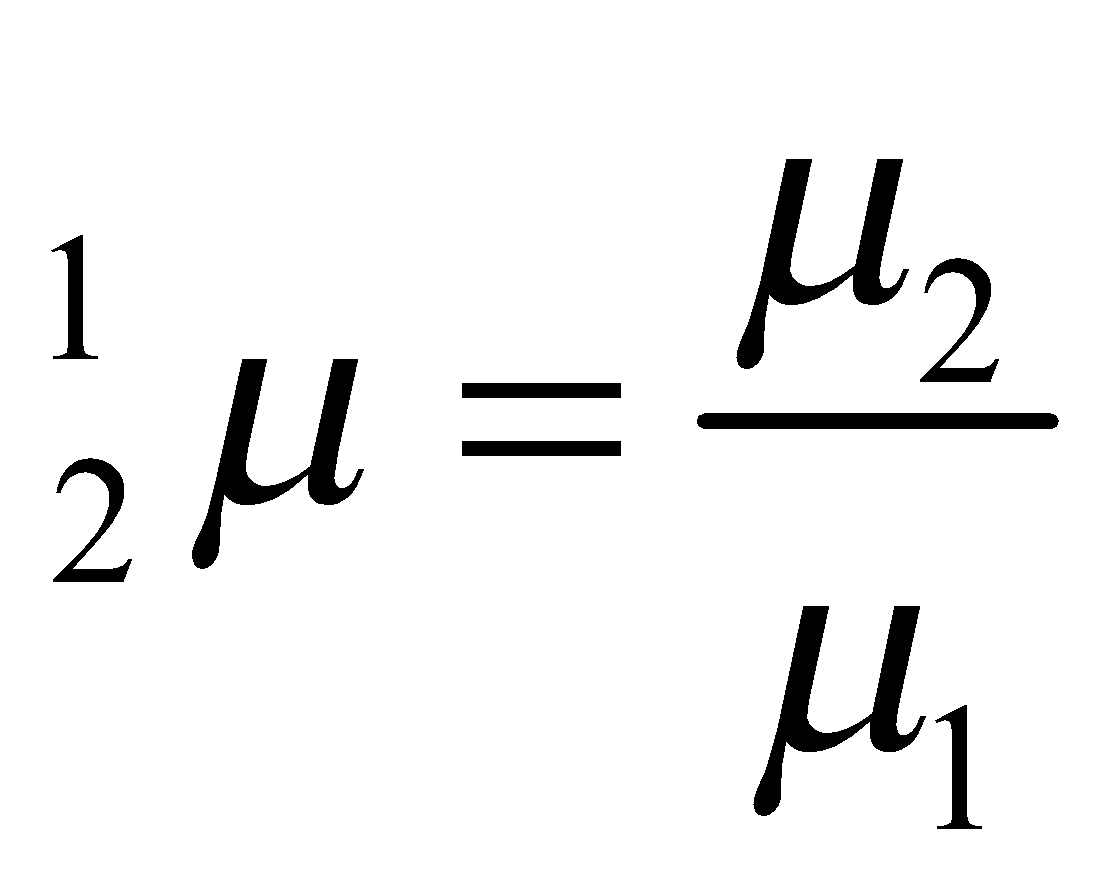
In the above formula μ2 is refractive index of lens whereas μ1 is the refractive index of surrounding medium.
R1 is the radius of curvature of the lens reached first by light
R2 is the radius of curvature of the other surface.
Magnification : m = v/u
This relation holds for both convex and concave lenses for real as well as virtual images.
Power of a lens P = reciprocal of focal length expressed in metres.
i.e., .
.
i.e.,
Its unit : dioptre(D).
Note:- To solve numerical problems use sign conventions while substituting values in above equations.
Equivalent focal length of two lenses separated by distance d
Equivalent focal length of lens-mirror combination
In such a case, the ray of light suffers two refraction from the lens and one reflection from the mirror. The combination behaves as a mirror whose focal length is given by
f1 = focal length of lens, fm = focal length of mirror
It is important that in the above formula, we cannot apply the sign conventions of Cartesian system rather following sign conventions are followed.
Focal length of a converging lens / mirror is taken as positive and focal length of diverging lens/mirror is taken as negative.
Focal Length by Displacement Method
where D = distance between an object and screen
and d = distance between two positions of lens.
Aperture of a lens : With reference to a lens, aperture means the effective diameter of its light transmitting area. So the brightness i.e. intensity of image formed by a lens which depends on the light passing through the lens will depend on the square of aperture i.e. I ∝ (aperture)2
COMBINATION OF LENSES
- If a lens of focal length f is cut in two equal parts as shown in figure, each part will have focal length = f
- If the above parts of lens are put in contact as shown then the resultant focal length will be,
- If the two parts are put as shown, then L will behave as converging lens of focal length f while the other (L´) divergent of same focal length,
∴ P = 0
- If a lens of focal length f is divided into equal parts as shown, then each part will have focal length f',
i.e.
i.e., each part will have focal length 2f.
- If these parts are put as shown, then the resultant focal length of the combination will be
REFRACTION THROUGH A PRISM
Prism is a transparent medium whose refracting surfaces are inclined to each other.
The angle of deviation is given by δ = i + i′ – A
where A= angle of prism. For δ to be minimum, i = i′ and r = r′
δm = A(μ – 1)
Refractive index of prism, 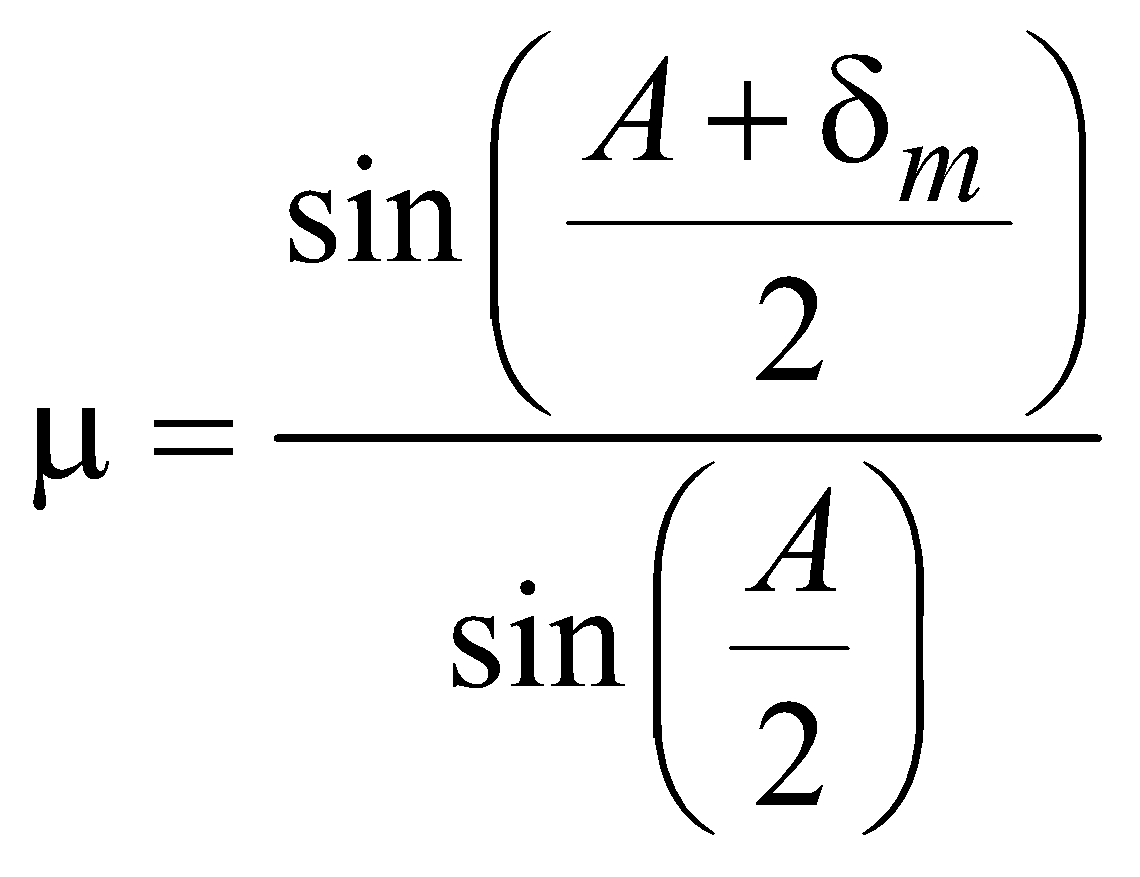
where δm = minimum angle of deviation
If angle of prism A is small, than δm is also small.
Plot of angle of deviation (δ) versus angle of incidence (i) for a triangular prism.
DISPERSION
It is the breaking up of white ray of light into its constituents colours VIBGYOR. The band of seven constituent colours is called spectrum.
Angular dispersion : It is defined as the difference of deviations suffered by the extreme colours.
i.e.,  [For thin prism]
[For thin prism]
Dispersive power : It is defined as the ratio of angular dispersion to the mean deviation produced by the prism.
i.e.,  [For thin prism]
[For thin prism]
KEEP IN MEMORY
- A ray entering a prism of angle A will not emerge out of prism if
where θc = critical angle
- Maximum deviation through a prism will occur when angle of incidence is 90°.
For this prism 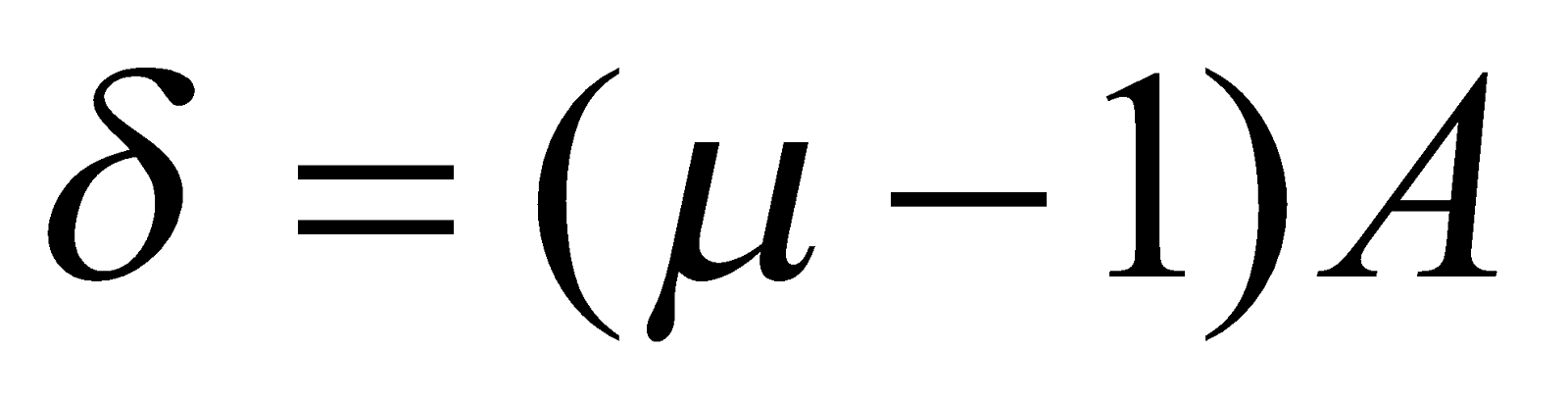
This shows that for a small angled prism, deviation is independent of angle of incidence.
- Angle of emergence of a prism is 90° (called grazing emergence) when angle of incidence
- A single prism produces deviation and dispersion simultaneously.
- Dispersion without deviation : When white light is incident on a combination of two prisms of different materials and of suitable angles placed opposite to each other, the emergent light may have only dispersion without any deviation ( of mean colour yellow).
For this to happen the conditions is
The net angular dispersion produced
- Deviation with dispersion
For this to happen  .... (1)
.... (1)
Net deviation 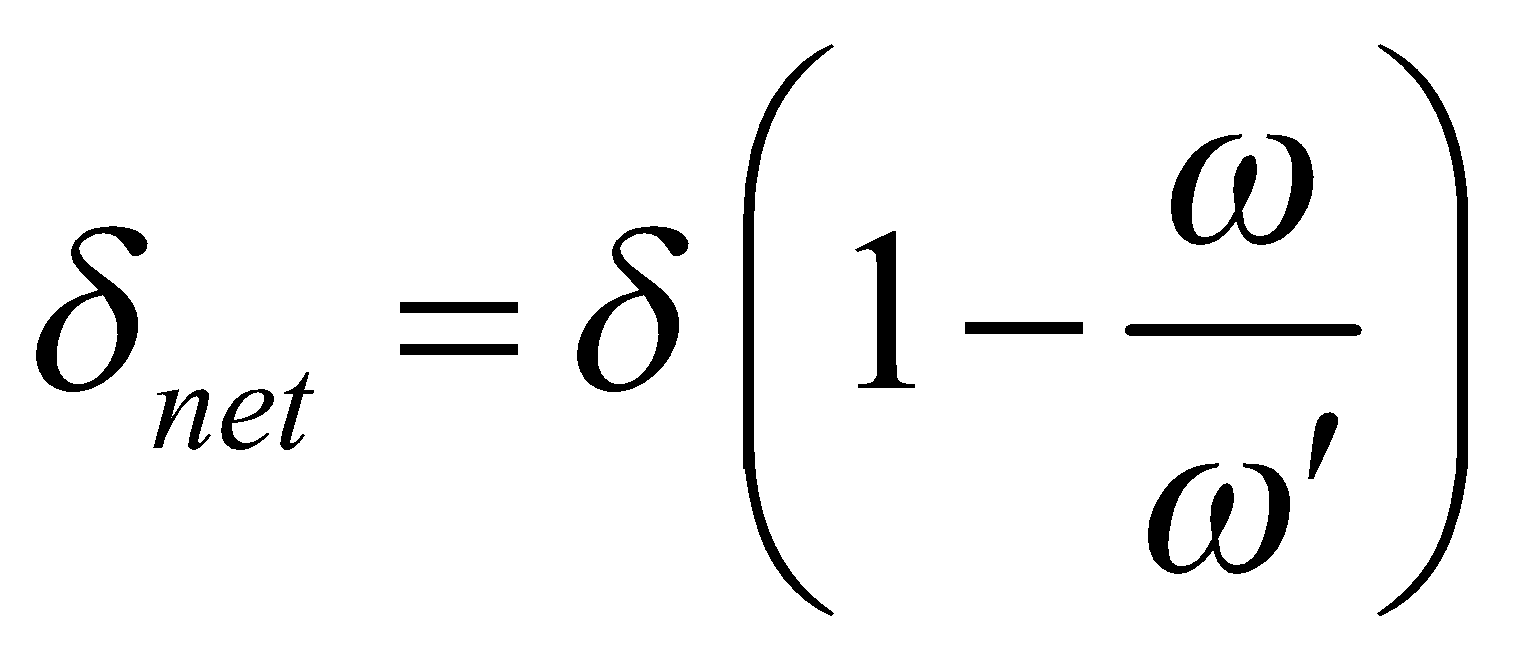
Equation (1) is said to be the condition of achromatism for combination of two prisms.
- Variation of refractive index of a medium with wavelength causing incident light to split into constituent colours is dispersion.
Cauchy’s equation : 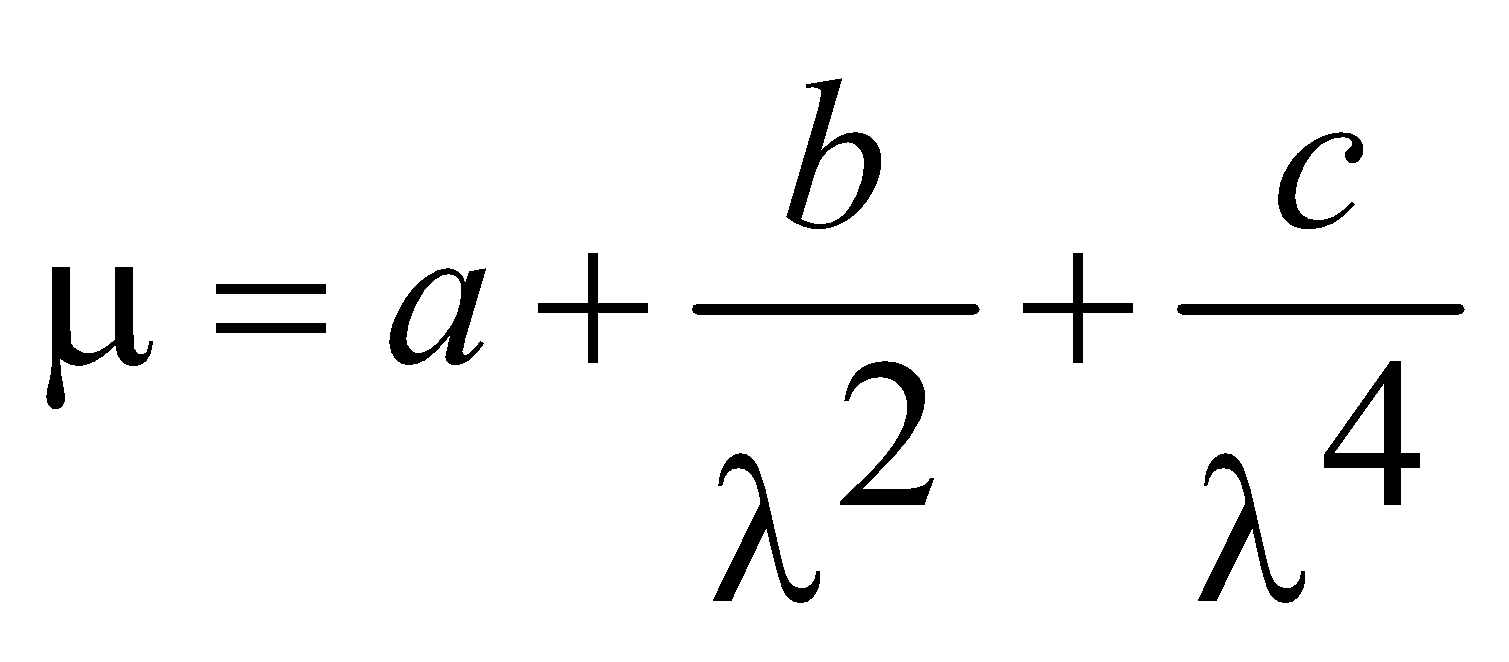 , where a, b and c are constants.
, where a, b and c are constants.
- Rayleigh scattering law explains blue colour of sky. Intensity of scattered light is proportional to 1/λ4. Hence the red light having highest value of λR scatters less.
- Rainbow can be observed if light source is behind and the droplets are in front of the observer, i.e. when the back of a person is towards the sun.
It is a consequence of dispersion of sunlight by water droplets due to a combinations of refraction and total internal reflection. If the rainbow is formed after one internal reflection in the droplets, it is called a primary rainbow. In this the violet ray emerges at an angle of 40.8º and red rays at an angle of 42.8º. If the rainbow is formed after two internal reflections, it is called a secondary rainbow. In this the violet rays emerge at 54º and red at 51º, i.e. the order of colours is reversed. The primary rainbow is brighter than the secondary.
- When a point source of light is placed at a depth h below the surface of water of refractive index m, then radius of bright circular patch on the surface of water is given by
- When a lens made up of glass is immersed in water, its focal length changes.
- For achromatic combination of these lenses in contact, the necessary condition is
- For two lenses separated by distance d, spherical aberration is minimum when d = f1 – f2.
- A convex lens forms a real image when the object is placed beyond focus. When the object is placed between optical centre and focus, convex lens forms a virtual image.
- A concave lens always form a virtual image for a real object.
- A lens is called thin when the thickness of the lens is small compared to the object distance, image distance, radii of curvatures of the lens. In the case of thick lens, the problem has to be solved using formula for each interface one by one.
COMMON DEFAULT
🗶 Incorrect : Using thin lens formula while the lens given in the numerical problem is thick.
✔ Correct : The lens formula  and lens maker’s formula
and lens maker’s formula  are valid only for thin lenses.
are valid only for thin lenses.
OPTICAL INSTRUMENTS
SIMPLE MICROSCOPE
It is known as simple magnifier & consist of a convergent lens with object between its focus & optical centre & eye close to it.
The magnifying power of a simple microscope (M.P.) is
Here
so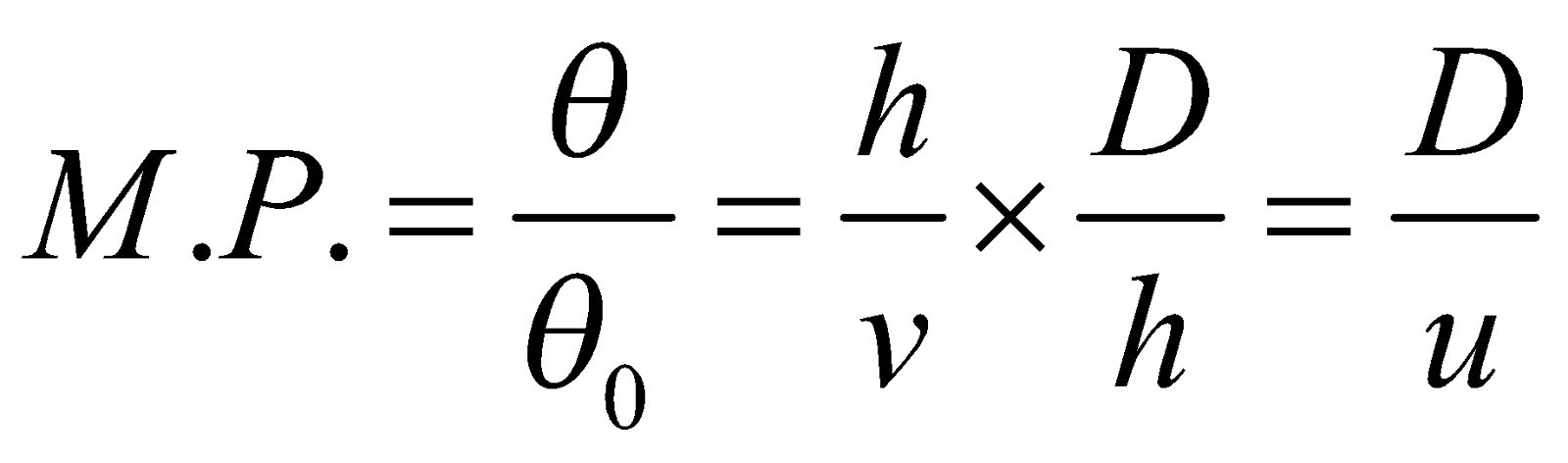
so
- If image is at infinity [far point] then from lens formula
In this case M.P. is minimum if eye is least strained.
- If image is at D [near point] then u = –D
and from lens formula 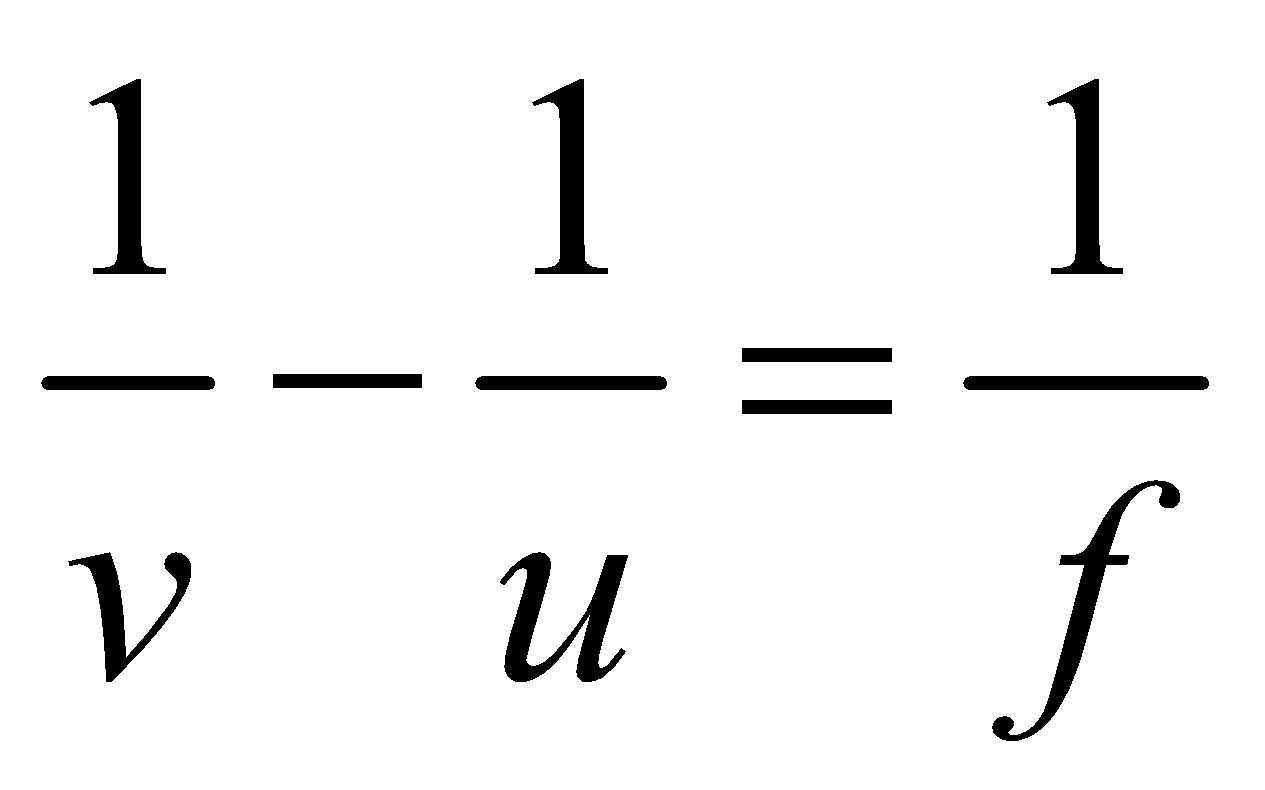
we get  so,
so, 
In this case M.P. is maximum and as final image is close to eye, eye is under maximum strain.
COMPOUND MICROSCOPE
M.P. of compound microscope is defined as
where  ,
, 
so 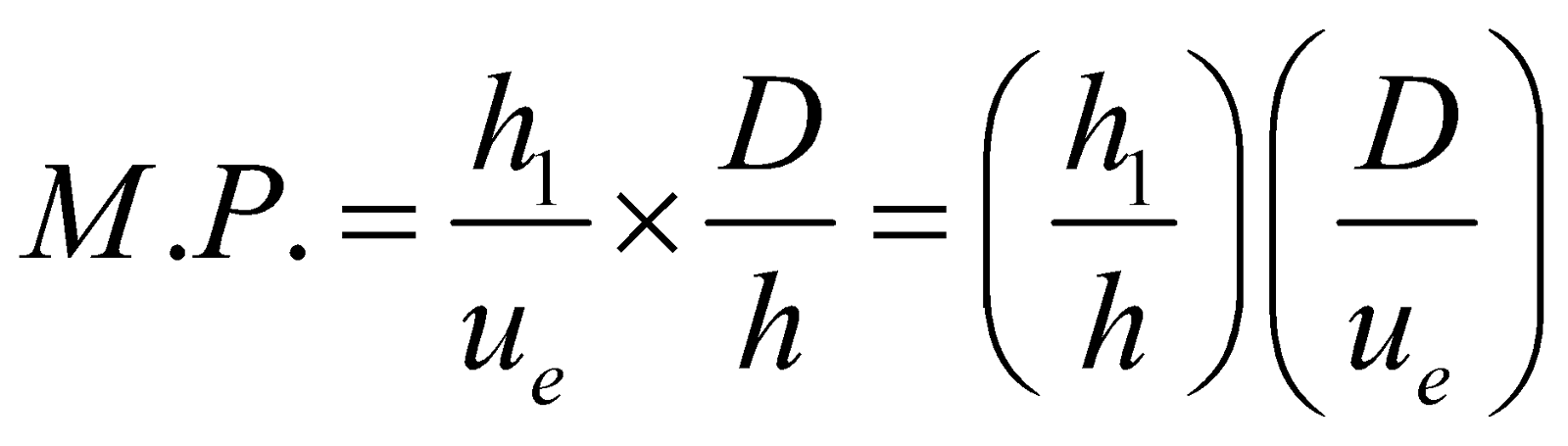
(since for objective  , as u is –ive)
, as u is –ive)
so 
- When image is formed at least distance of distinct vision
- When the final image is formed at infinity
ASTRONOMICAL TELESCOPE
- If the final image is formed at a distance D,
Length of tube is 
- If the final image is formed at infinity then
Length of tube is 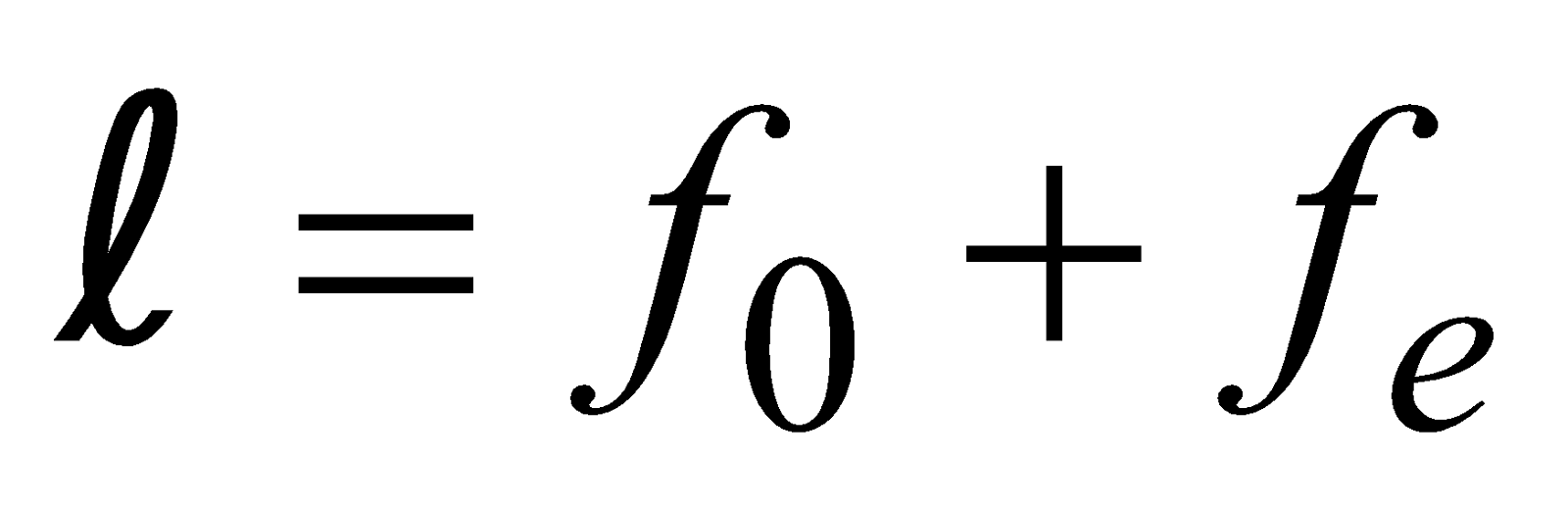
GALILEAN TELESCOPE
Length of tube L = fo – fe
TERRESTRIAL TELESCOPE
Length of tube L = fo + fe+ 4f, where f is the focal length of erecting lens, which is used in this telescope.
RESOLVING POWER OF MICROSCOPE AND TELESCOPE
- The resolving power of microscope is
where μ = refractive index of medium between object and objective of microscope and θ = angle subtended by a radius of the objective on one of the objects. (When both objects are not self luminous). - The resolving power of a telescope is
where a = diameter of objective of telescope.
EYE DEFECTS
Some common eye defects are myopia, hypermetropia, astigmatism and presbyopia.
Astigmatism : It is due to different curvature of cornea in horizontal and vertical plane. It is corrected by using cylindrical lens.
Presbyopia : The eye with this defect cannot see near objects as well as far off objects clearly.
PHOTOMETRY
Ray optics is based on the assumption that light travels along straight line.
Luminous flux (φ) of a source of light = amount of visible light energy emitted per second from the source. The SI unit of luminous flux (φ) is lumen.
Luminous intensity (I) of a light source = luminous flux emitted per unit solid angle in any direction. Its SI unit is candela.
Luminous intensity, 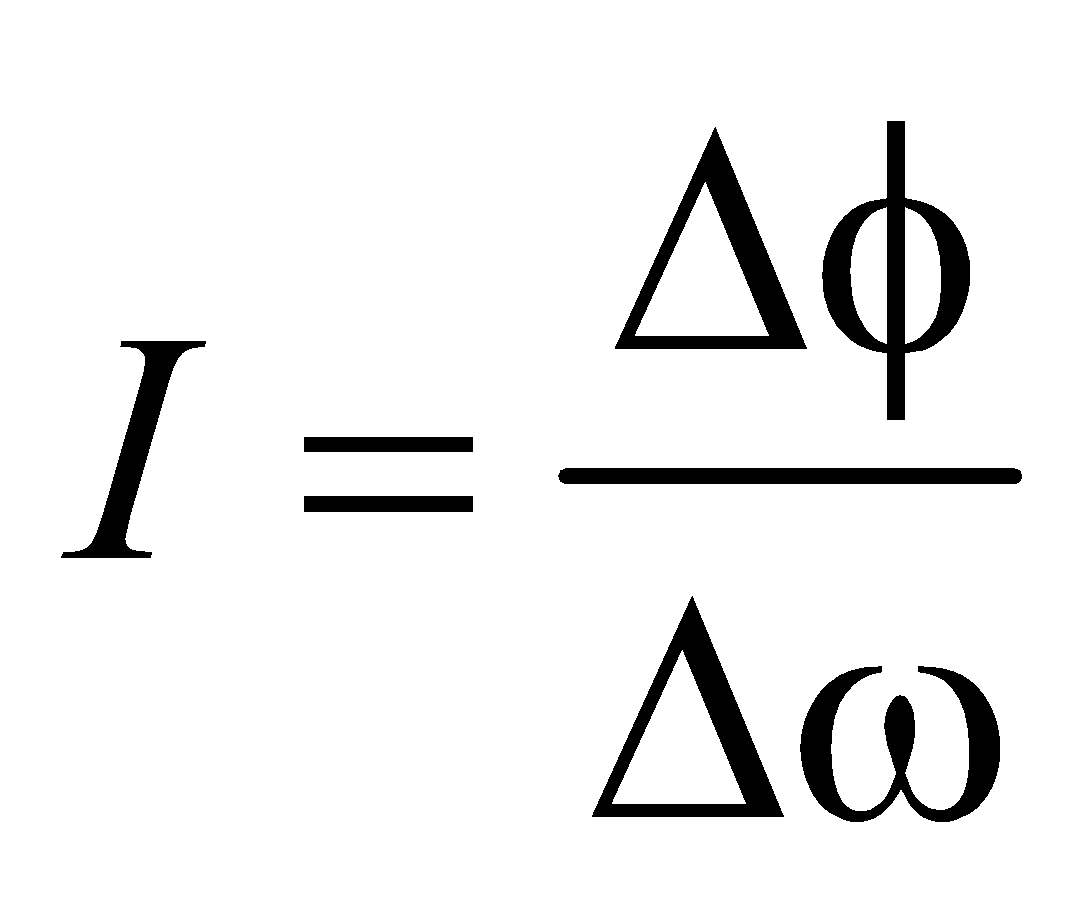
For isotropic point source,
Solid angle,
(where ΔA = 4πr2 = total surface area of sphere of radius r)
so  or φ = 4π. I
or φ = 4π. I
Solid angle
We know that arc of a circle subtends an angle θ on the centre of circle O
- The unit of θ (plane angle) is radian.
Similarly in the case of a sphere, the surface area of sphere subtends an angle on the centre of sphere O, which is called solid angle & is denoted by ω.
Let radius of sphere is r and a small area ΔA on its surface subtends a solid angle ω at the centre then
The unit of solid angle is steradian. If in eq (ii)
ΔA = r2 , then ω = 1 steradian
If ΔA = 4πr2 (total surface area of sphere) then ω = 4π steradian.
Illuminance (E) of a surface is the luminous flux incident normally on unit area of the surface. Its unit is lux.
For point source, the total normal area will be 4πr2,
so 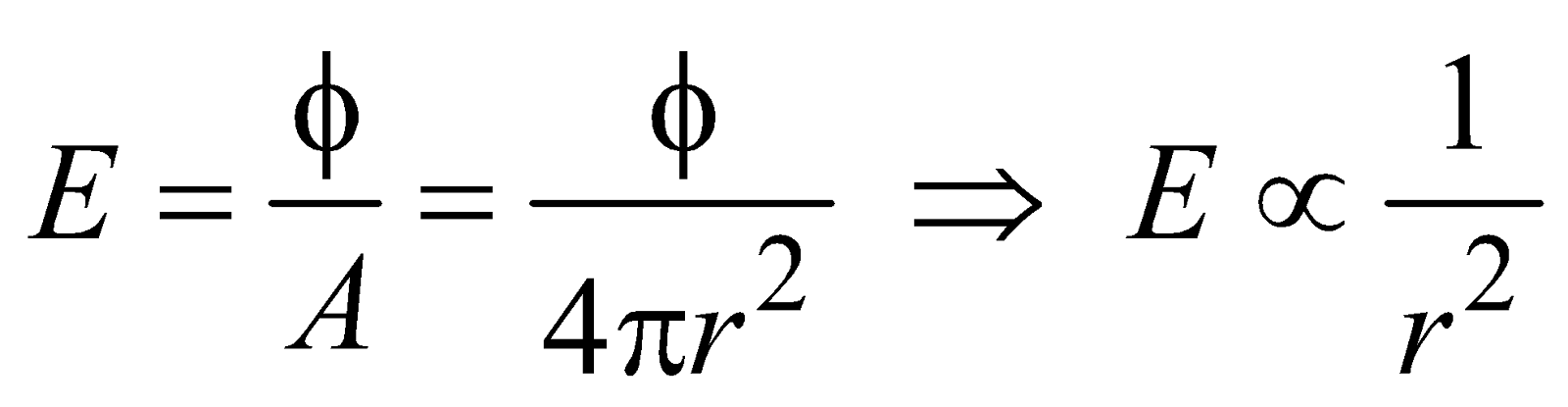
Luminance or brightness of a surface is the luminous flux reflected into our eyes from unit area of the surface. The unit of Brightness is lambert.
INVERSE SQUARE LAW FOR ILLUMINANCE
Let S is a unidirectional point source, whose luminous intensity is I. It has some surface ΔA at distance r from source S.
Let central ray of source s falls perpendicularly on surface ΔA, then luminous flux Δφ is given by
Δφ = I×Δω ...(i)
where 
or  or
or  ...(iii)
...(iii)
where E is called illuminance or intensity of illumination.
If in eq. (iii) I is constant for a given source then

So intensity of illumination of any source is inversely proportional to square of the distance between light source & surface. This is called inverse square law.
LAMBERT'S COSINE LAW FOR ILLUMINANCE
Let S is unidirectional point source & its luminous intensity is I. There is a surface of area ΔA at distance r from S, which is kept in such a way that light from S falls obliquely on it and central ray makes an angle θ with normal to ΔA.
Then by fig. ΔA′ = ΔA cos θ
According to definition of luminous intensity :
Δφ = I × Δω
where 

or 
For any given source (I constant) & at a fixed distance (r constant) E ∝ cos θ
i.e., the, intensity of illumination of a surface is proportional to the cosine of angle of the inclination of the surface. This is called Lambert’s cosine law. As θ increases, cos θ decreases & consequently E decreases.
θ is the angle between normal to the area and direction of light propagation.










