Binomial Theorem | Mathematics Notes for IITJEE Main

BINOMIAL THEOREM

INTRODUCTION

• An expression containing two terms connected by + or – sign is called a BINOMIAL. For example, a + b,  , a – y2, 2b – 3c etc. are binomial expressions.
• Similarly, an expression containing three terms is called a TRINOMIAL. In general, expressions containing more than two terms are called MULTINOMIALS.
• The general form of the binomial expression is x + a and the expansion of (x + a)n, n being a positive integer, is called the BINOMIAL THEOREM. Sir Isaac Newton first gave this theorem.

BINOMIAL THEOREM FOR POSITIVE INTEGRAL INDEX

Statement : If , then

PROPERTIES OF THE EXPANSION OF (x + a)n

1. The number of terms in the expansion of (x + a)n is n + 1, i.e., one more than the index n.
2. The sum of the powers of x and a in each term is n, thus it is a homogeneous expansion.
3. The (r + 1)th term in the expansion is nCr xn – r ar and is called the general term, i.e., Tr + 1 = nCr xn – r ar.
4. nC0, nC1, nC2 ......, nCn are coefficients of the successive terms and are called the binomial coefficients.
5. The binomial coefficients of terms equidistant from the beginning and end are same as nCr = nCn – r
6. The binomial expansion is briefly written as.
7. Putting –a for a, we have

The terms in this expansion are alternatively positive and negative and the last term is positive or negative according as n is even or odd.

8. Putting x = 1 and a = x in the expansion of (x + a)n, we have

This is expansion of (1 + x)n is ascending powers of x.

9. Putting a = 1 in the expansion of (x + a)n, we have

This is expansion of (1 + x)n is descending powers of x. The coefficient (r + 1)th term and the coefficient of xr in (1 + x)n is  or , both being equal.

10. The kth term from the end in the expansion of (x + a)n is
    (n – k + 2)th term from the beginning.
11. We note that 

= 2 [sum of  the terms at even places]

= 2 [sum of the term at odd places]

MIDDLE TERM OF TERMS IN THE EXPANSION OF (x + a)n

The number of terms in the expansion of (x + a)n is n + 1. Therefore,

If n is even then there is only one middle term, viz. th term.

If n is odd then there are two middle terms, viz. th and th terms.

GREATEST COEFFICIENT IN THE EXPANSION OF (x + a)n

The coefficients are where the coefficient of the general term is nCr. We have to find the value of r for which nCr has the greatest value. We know that if n is even nCr is greatest when and if n is odd nCr is greatest for or.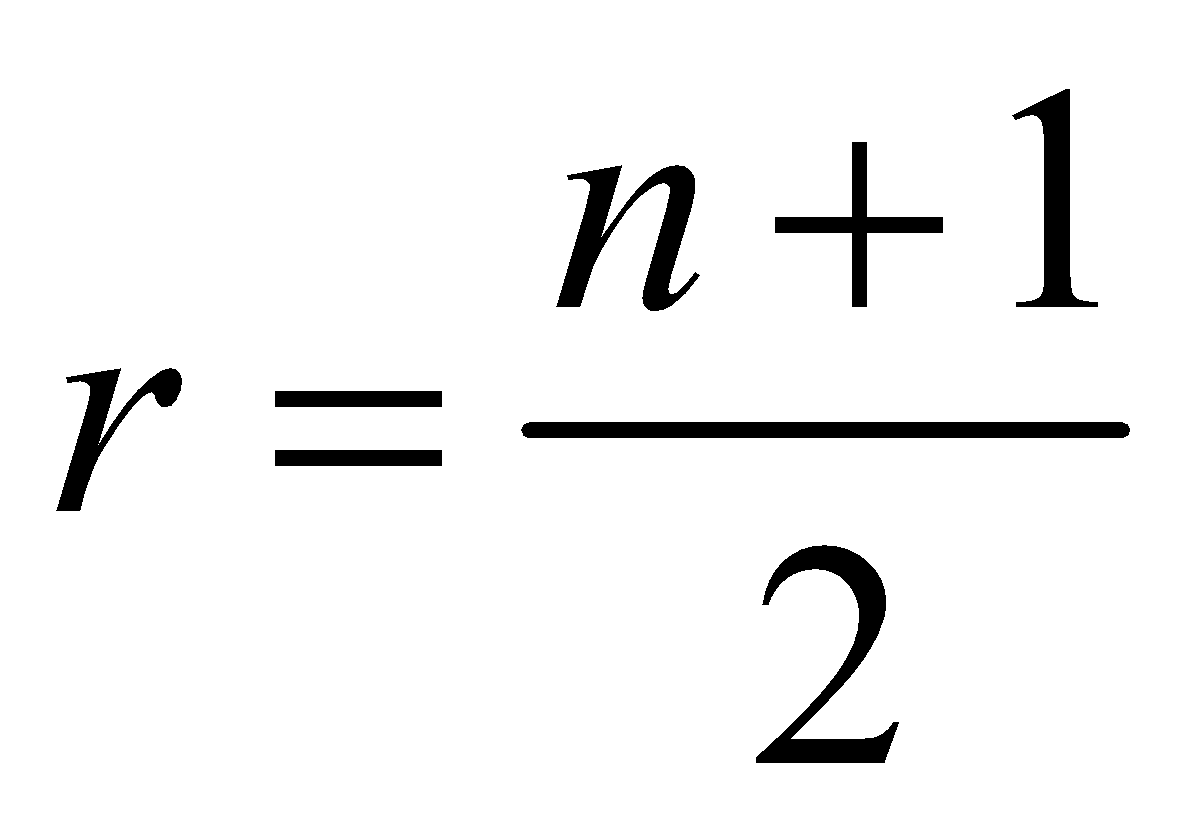

Hence, if n is even the greatest coefficient is 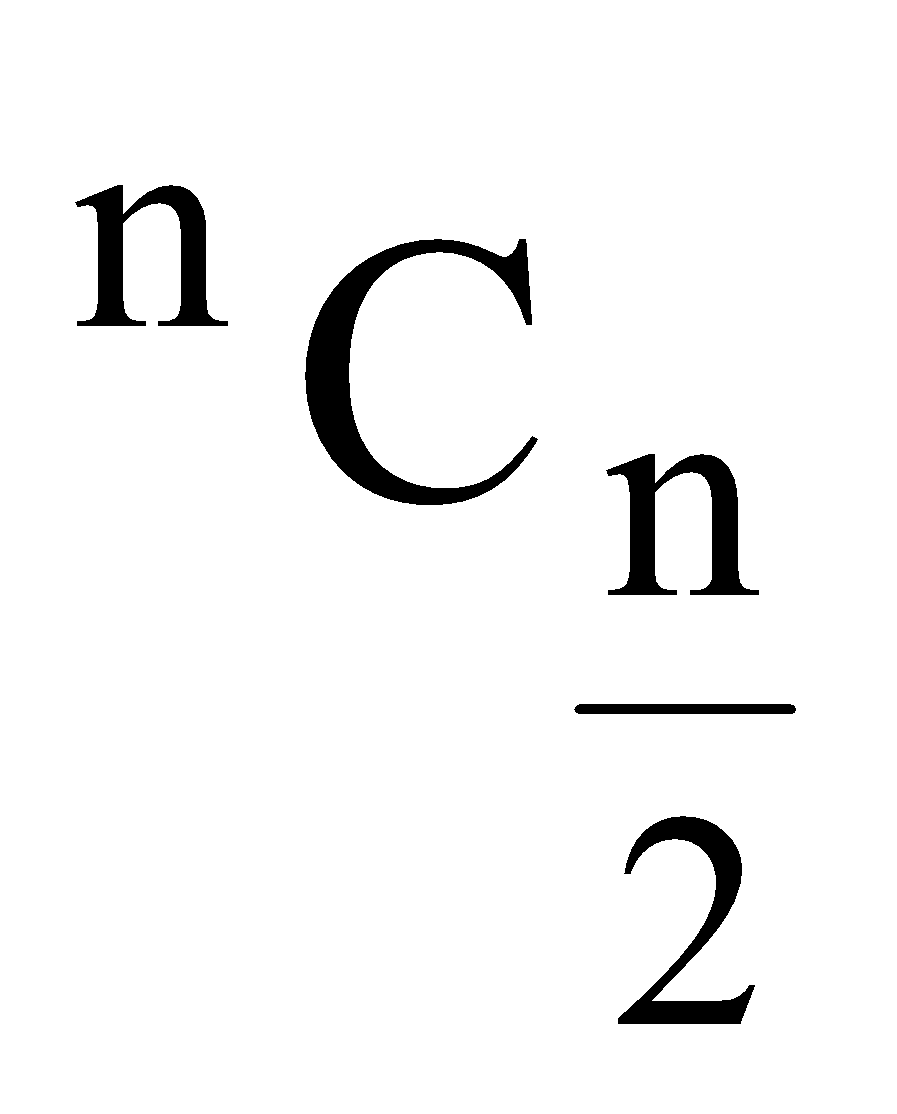, and if n is odd, the greatest coefficient is nC(n – 1)/2 or nC(n + 1)/2 both being equal.

NUMERICALLY GREATEST TERM IN THE EXPANSION OF (x + a)n

Let Tr and Tr + 1 be rth and (r + 1)th terms respectively in the binomial expansion of (x + a)n. Assume that x and a are positive

Then Tr =  nCr – 1 xn – r + 1 ar – 1 and Tr +  1= nCr xn – r ar

or

Hence,

According as i.e., according as

i.e., according as i.e., according as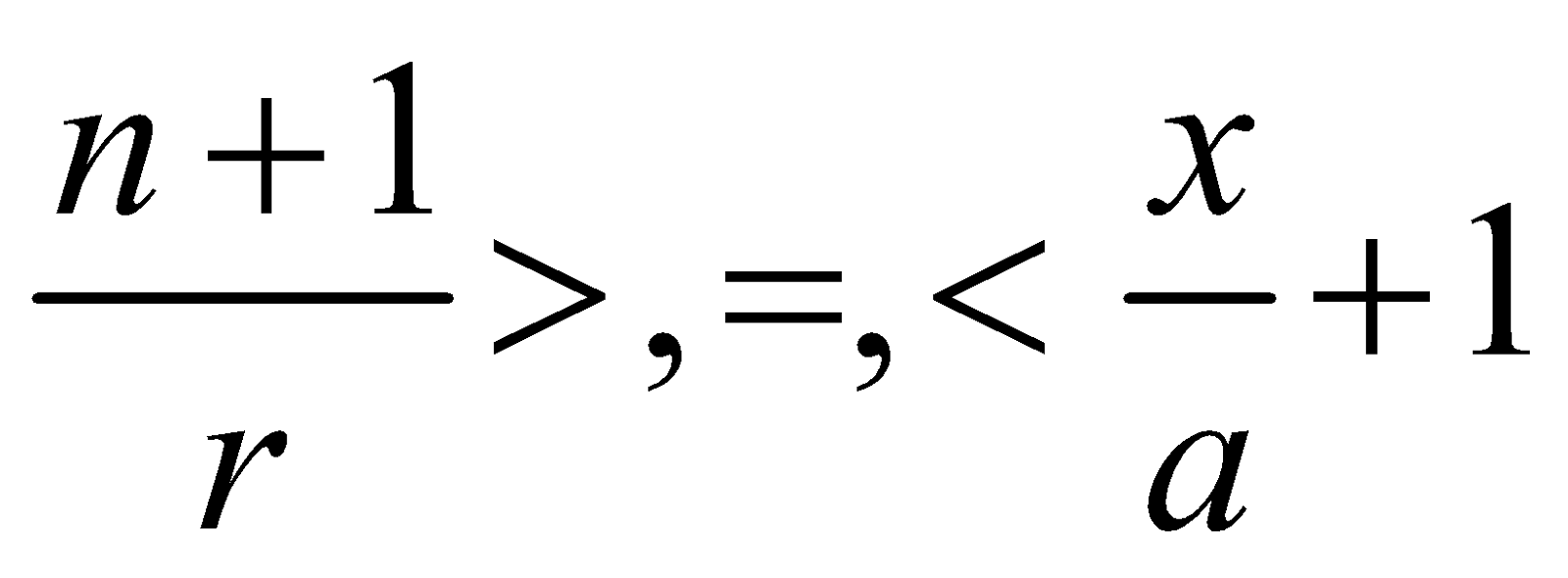
i.e., according as ……….(I)

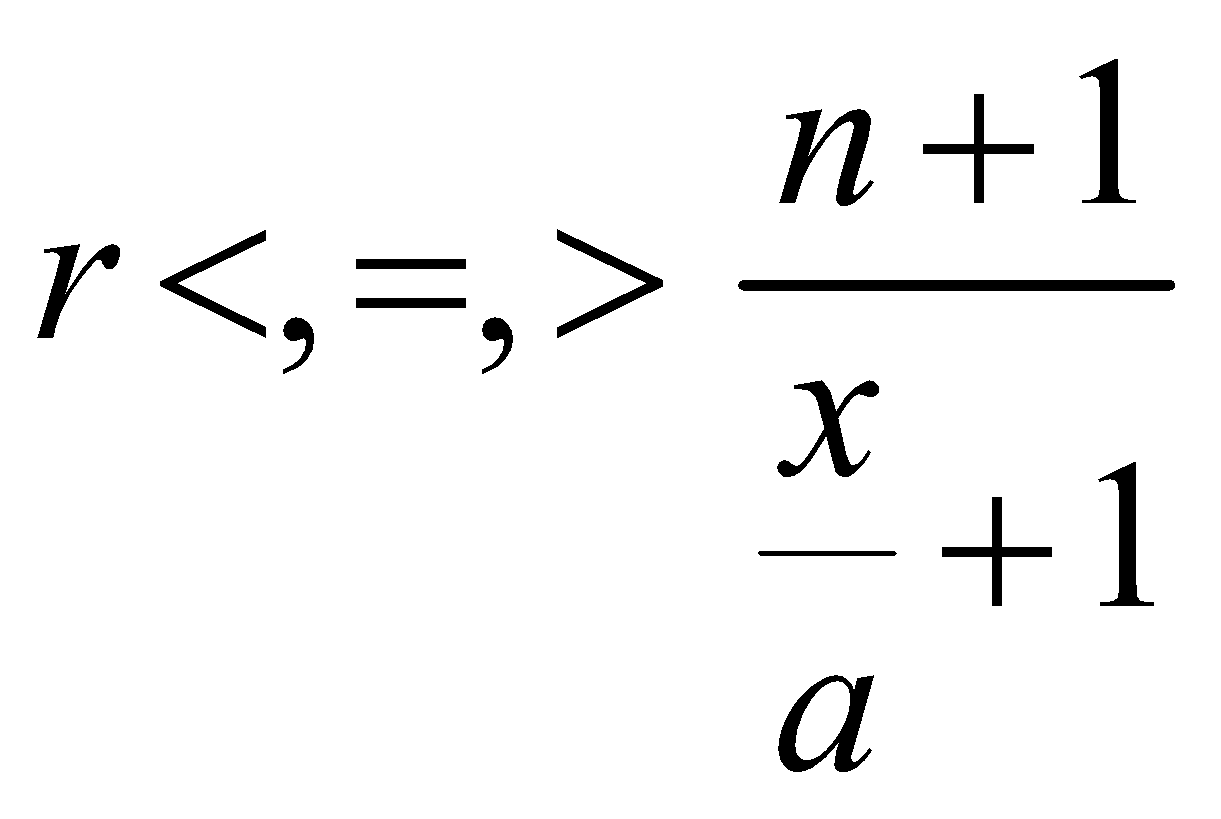Now the value of may be an integer or fraction. Therefore, two cases arise.

Case I : When is an integer, say, p

From (I), Tr + 1 > Tr if r < p, otherwise Tr + 1  Tr

∴ For  r = 1, 2, ...., p – 1 we have Tr + 1 > Tr,

For r = p we have Tr + 1 = Tr

And for r = p + 1, p + 2, ..., we have Tr + 1 < Tr.

∴ Hence in this case Tp = Tp + 1 and these are greater than any other term.

Case II : When is not an integer.

Let m be the integral part of 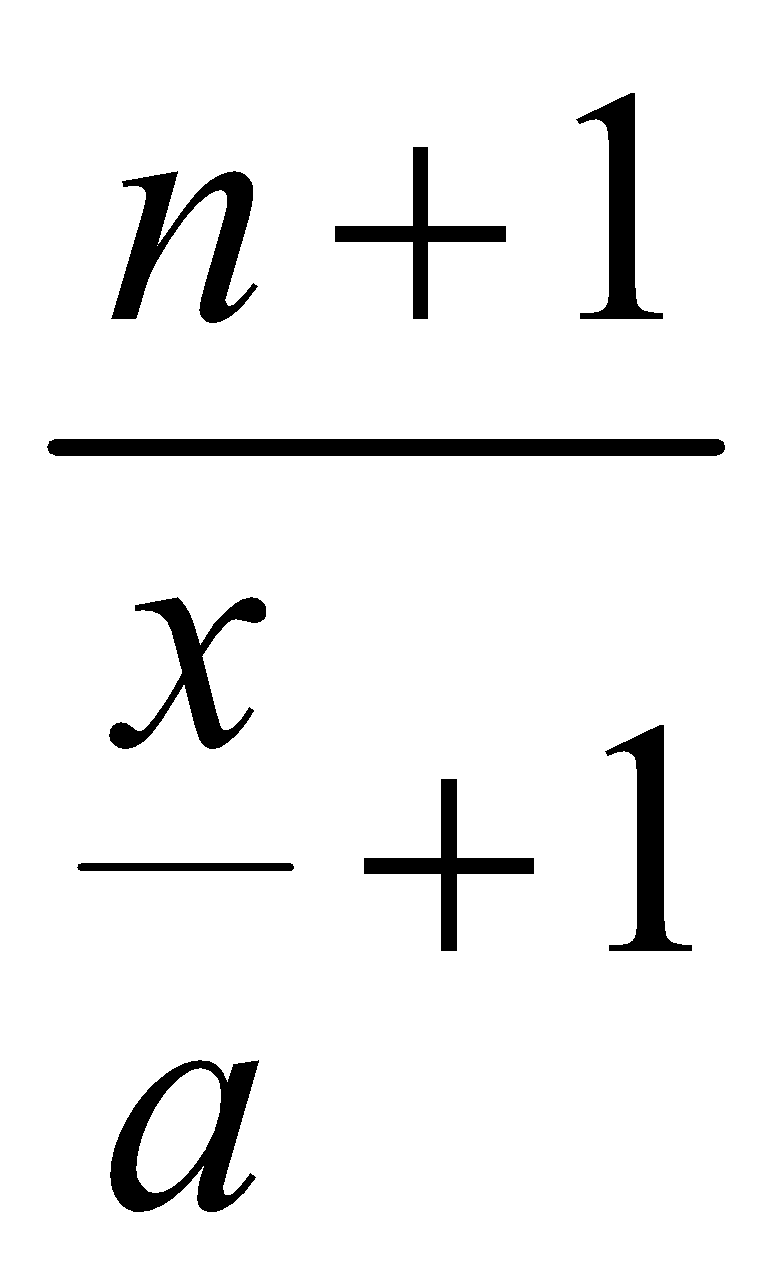, i.e.

Then from (I),  Tr + 1 > Tr for r = 1, 2, 3, ....., m and Tr + 1 < Tr for r = m + 1, m + 2, .......

Hence, in this case the Tm + 1 is the greatest term.

PROPERTIES OF BINOMIAL COEFFICIENTS

We have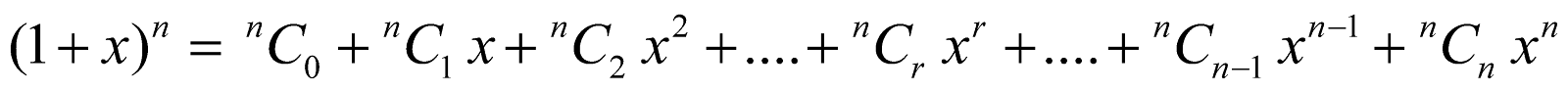

Also,

Let us denote 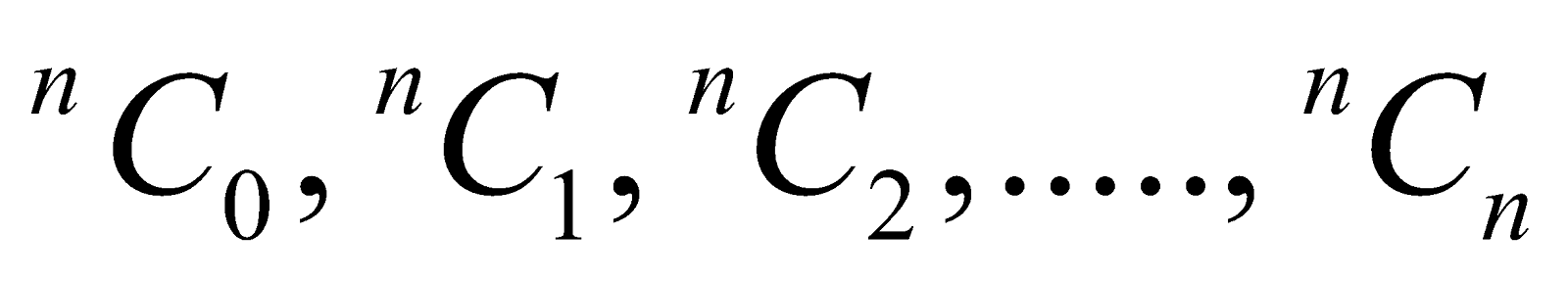by C0, C1, C2,...., Cn respectively.

Then the above expressions become

and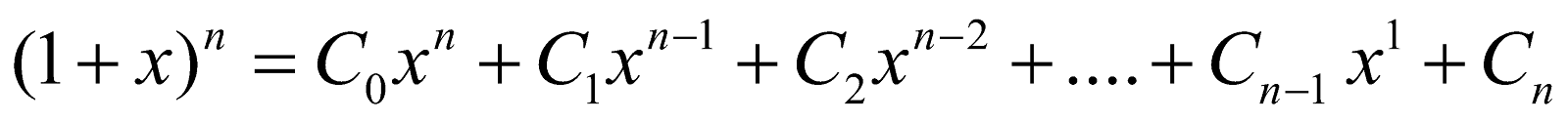

C0, C1, C2,....,Cn are called the binomial coefficient and have the following properties:

1. In the expansion of (1 + x)n the coefficient of terms equidistant from the beginning and end are equal.

The coefficient of (r + 1)th term from the beginning is nCr. The (r + 1)th term from the end is (n – r + 1)th term from the beginning. Therefore, its coefficient is nCn – r.

But nCr = nCn – r

Hence the coefficient of terms equidistant from the beginning and end are equal.

2. The sum of the binomial coefficient in the expansion of (1 + x)n is 2n.

Putting x = 1 in (1 + x)n = C0 + C1 x + C2 x2 + ..... + Cr xr + .... + Cn xn, we get  

C0 + C1 + C2 + ..... + Cn = 2n or.

3. The sum of the coefficient of the odd terms is equal to the sum of the coefficient of the even terms and each is equal to
   2n – 1 i.e., C0 + C2 + C4 + ...... = C1 + C3 + C5 + ..... = 2n – 1

Putting x = 1 and –1 respectively in the expansion.

,

we get C0 + C1 + C2 + C3 + ..... + Cn – 1 + Cn = 2n

and C0 – C1 + C2 – C3 + .... + (–1)n Cn = 0

Adding and subtracting these two equations, we get

C0 + C2 + C4 + .... = C1 + C3 + C5 + .... = 2n – 1

1 . C1 + 2 . C2 + 3 . C3 + .... + n . Cn = n . 2n – 1 or  

we have

Differentiating both sides w.r.t. x and putting x = 1, we get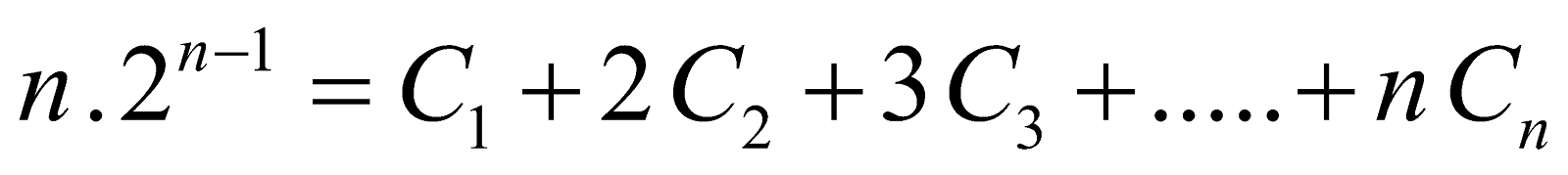

EXTRA IMPORTANT RESULTS

1. 
2. that is, and
3. 
4. 
5. 
6. 
7. 
8. 
9. 

Mathematics Study Notes

• Sets, Relations and Functions
• Trigonometric Ratios and Identities
• Trigonometric Equations and Inequations
• Properties of Triangles, Height and Distances
• Principle of Mathematical Induction, Permutation and Combination
• Complex Numbers
• Quadratic Equations
• Linear Inequalities
• Sequences and Series
• Binomial Theorem
• Infinite Series
• Points & Straight Lines
• Pair of Straight Lines
• Circles
• Parabola
• Ellipse and Hyperbola
• Mathematical Reasoning
• Statistics
• Probability Basic
• Functions
• Inverse Trigonometric Functions
• Matrices
• Determinants
• Limits, Continuity and Differentiability
• Differentiation and Application of Derivatives
• Indefinite Integration
• Definite Integration and Applications
• Differential Equations
• Vector Algebra
• Three Dimensional Geometry
• Probability Advanced

Study Notes for JEE Main/JEE Advanced/BITSAT