Circles | Mathematics Notes for IITJEE Main

CIRCLES

CIRCLES

A circle is the locus of a point, which moves such that its distance from a fixed point is always constant.

The fixed point in called the CENTRE of the circle and the constant distance is called the RADIUS of the circle.

EQUATION OF A CIRCLE WITH CENTRE C (h, k) AND RADIUS a

Let P(x, y) be the variable point, then by definition

...(1)

Equation (1) is the required equation of the circle.

IMPORTANT FORMS

1. If centre be the origin, the equation (1) is.
2. If the circle touches the x-axis, then a = | k | and the equation is of the form .
3. If the circle touches the y-axis then a = | h | and the equation of the circle is of the form
4. If the circle touches both the axis, then a  = | h | = | k |, and the equation of the circle is of the form

5. The equation of the circle, which passes through the origin and cuts the intercepts of lengths a and b on x-axis and y-axis respectively is x2 + y2 – ax – by = 0.

Its centre is and radius =

6. The equation of the circle, which is described with the points A (x1, y1) and B (x2, y2) as the extremities of a diameter is.

Centre is 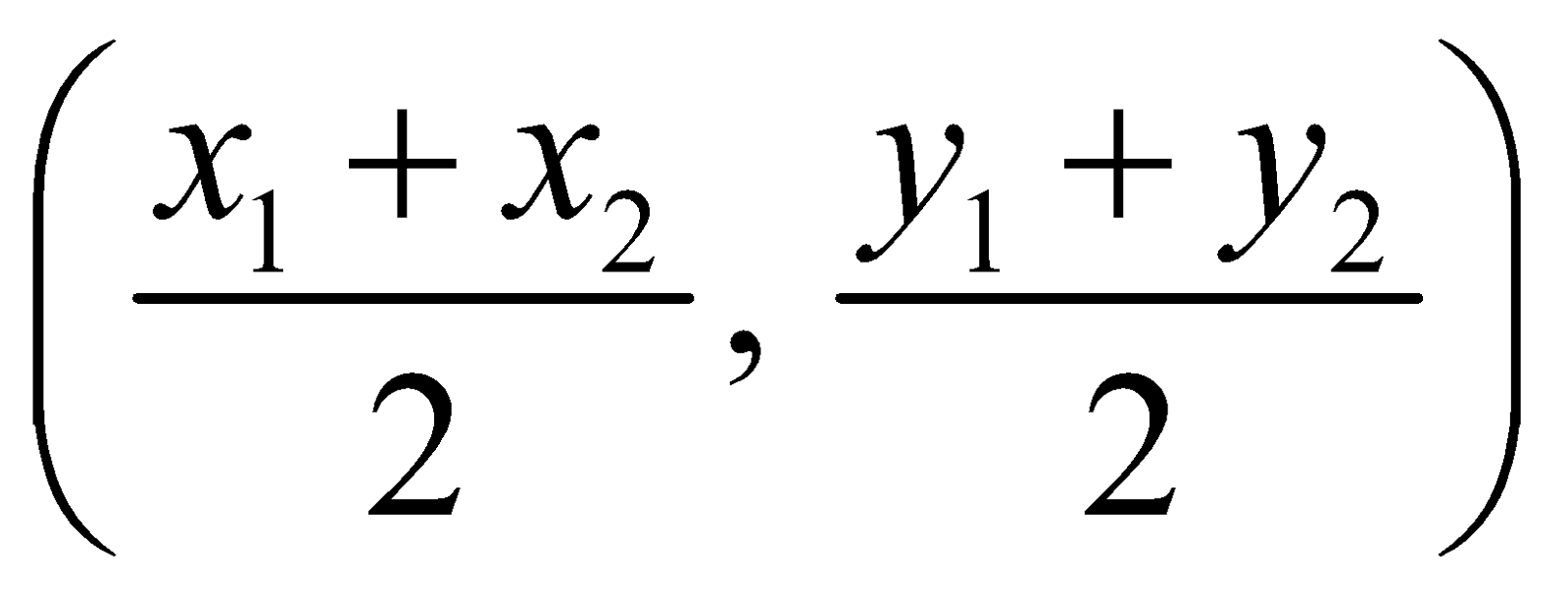and

Radius =

GENERAL EQUATION OF A CIRCLE

Expanding the equation (1), we get

This equation is of the form

....(2)

where g = – h, f = – k and c = h2 + k2 – a2

∴ The centre of the circle represented by (2) is (–g, –f)

The radius of the circle represented by (2) is

CIRCLE THROUGH THREE POINTS

The equation of the circle through three non-collinear points (x1, y1), (x2, y2), (x3, y3) is

Note : A unique circle can always be drawn through three non-collinear points.

IMPORTANT RESULTS

1. The general equation of the circle (2) represents a real circle in the plane if
2. If g2 + f2 – c = 0, the equation (2) is of the form, i.e., x = –g and y = –f. The equation (2) represents a point (–g, –f) or a point circle.
3. If, the equation (2) does not represent any circle or any point in the plane (or represents imaginary circle).
4. The general equation of second degree

....(3)

represents a circle if a = b and h = 0, i.e., coefficient of x2 = coefficient of y2 and coefficient of xy = 0.

The equation (3) then becomes, ax2 + ay2 + 2gx + 2fy + c = 0 , which can be reduced to form (2) if divided by a.

EQUATION OF A CIRCLE IN PARAMETRIC FORM

Let the equation of a circle in standard form be

From the figure, ...(1)

where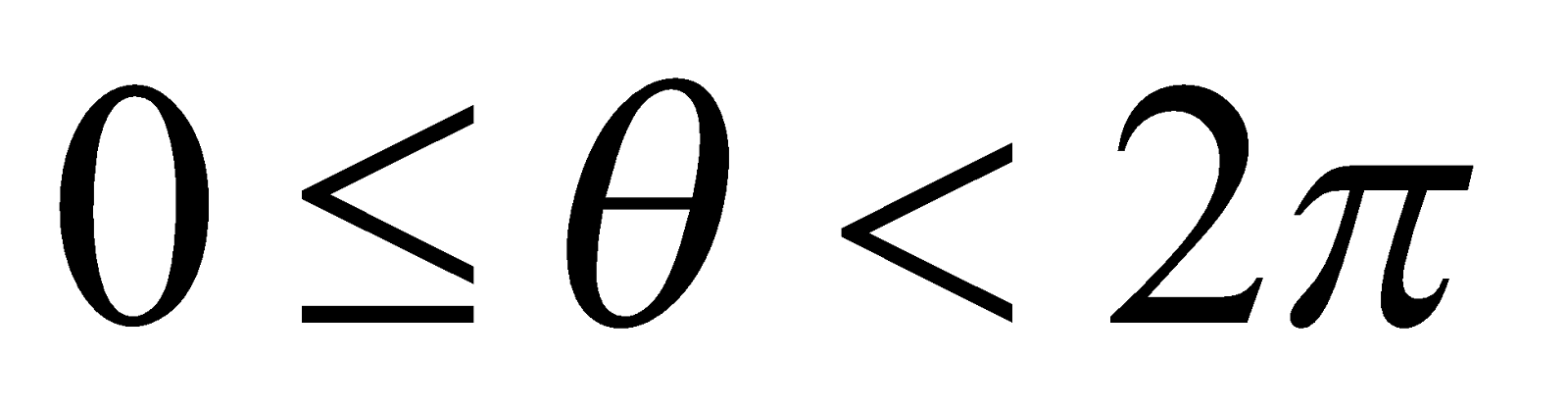

The equation (1) represents the parametric equation of the circle, θ being the parameter.

The parametric equation of the circle given by

is  ....(2)

where

INTERCEPTS OF A CIRCLE ON THE COORDINATE AXES

Consider the general form of a circle x2 + y2 + 2gx + 2fy + c = 0

For the intercept on x-axis, we put y = 0, we have x2 + 2gx + c = 0

Which is a quadratic in x, its roots, say x1 and x2 provide the coordinates of the points of intersection of the points of intersection of the circle and the x-axis A(x1, 0) and B (x2, 0). We have

[Relation between roots and coefficients of an equation].

The intercept of the circle on x-axis

AB = | x2 – x1 | =

Similarly the intercept on y-axis

RESULTS

1. The circle intersects x-axis in two real points if g2 –  c > 0.
2. The circle touches the x-axis of g2 – c = 0.
3. The circle neither touches nor intersects the x-axis if g2 –  c < 0. Similarly with y-axis.

POSITION OF A POINT WITH RESPECT TO A CIRCLE

Let the equation of a circle be x2 + y2 + 2gx + 2fy + c = 0 or S (x, y) = 0 and P (x', y') be a point in the plane.

The point P lies outside, on or inside the circle according as the distance from the centre,

CP >, = , or < radius, i.e., >, =, or < 0

or according as

S(x', y') >, =, or < 0, or S' >, =, or < 0 ...(3)

Where

Hence, If S(x', y') = 0 or S' = 0, P lies on the circle.

If S(x', y') > 0 or S' > 0, P lies outside the circle.

If S (x', y') < 0 or S' < 0, P lies inside the circle.

INTERSECTION OF A LINE AND A CIRCLE

Let the equation of circle be x2 + y2 = a2 and the line be y = mx + c

Eliminating y from the two equation,

we have

    .....(4)

This is a quadratic equation in x, with real coefficients. Its roots x1 and x2 provide the abscissae of the points of intersection A (x1, y1) and B (x2, y2). The discriminant of equation (4) is

SOME IMPORTANT DEDUCTIONS

1. If , the line intersects the circle in two distinct points.
2. If , the line touches the circle.
3. If the line does not touch nor intersect the circle.
4. If the line intersects the circle in two distinct points, the length of chord cut inside the circle

AB =

or AB =

[(x1, y1) & (x2, y2) line on the line y = mx + c]

[Since, x1 and x2 are the roots of equation (4)]

...(5)

Alternatively we can use the following method also :

Let S be a circle with centre C and radius a. Let L be any line in the plane of the circle and d be the perpendicular distance from C to the line L, then

• L intersects S in two distinct points iff d < a
• L intersects S in one and only point iff d = a, i.e the line L touches the circle iff perpendicular distance from the centre of the line L is equal to radius of the circle.
• L does not intersect S iff d > a.

Remark : This method is always recommended if the equation of the circle is not of the standard form.

LENGTH OF INTERCEPT MADE BY A CIRCLE ON A LINE

If a line L meets a circle S, with centre C and radius a, in two distinct points and if d is the perpendicular distance of centre C from the line L, then the length of the intercept made by the circle on the line  

Note : If the points of intersection of a line L and a circle S are known, then the distance between these points is the required length of intercept and there is no need of using the above formula.

CONDITION OF TANGENCY

The line y = mx + c will touch the circle x2 + y2 =a2 if

c2 = a2 (1 + m2) or  c = ± a

Thus, for a given slope m, there are two parallel tangents to the circle given by

         ....(6)

and            ....(7)

The points of contact for the two tangents (6) and (7) are respectively, as per the equation of the tangent.

EQUATION OF TANGENT TO A CIRCLE AT A POINT ON IT

1. The equation of tangent to the circle x2 + y2 = a2 at a point (x', y') on it is
   xx' + yy' = a2 ....(8)
2. The equation of tangent to the circle x2  + y2 = a2  at the point is
3. The equation of tangent to circle (x – h)2 + (y – k)2 = r2 is

,

4. The equation of tangent to the circle x2 + y2 + 2gx + 2fy + c = 0 at a point (x', y') on it is xx' + yy' + g (x + x') + f (y + y') + c =0 ....(9)

Remark :

1. To find the equation of tangent to a curve (applicable to any quadratic curve) at a point (x', y') on it, we substitute xx' for x2; yy' for y2; for x; for y and for xy.
2. A straight line is a tangent to a given circle if length of perpendicular from centre to the line = radius
3. If a straight line is tangent to a circle (or any curve), then eliminating x (or y) from two equations we get a perfect square or coincident roots in y (or x)

TANGENT TO A CIRCLE FROM AN EXTERNAL POINT

Let 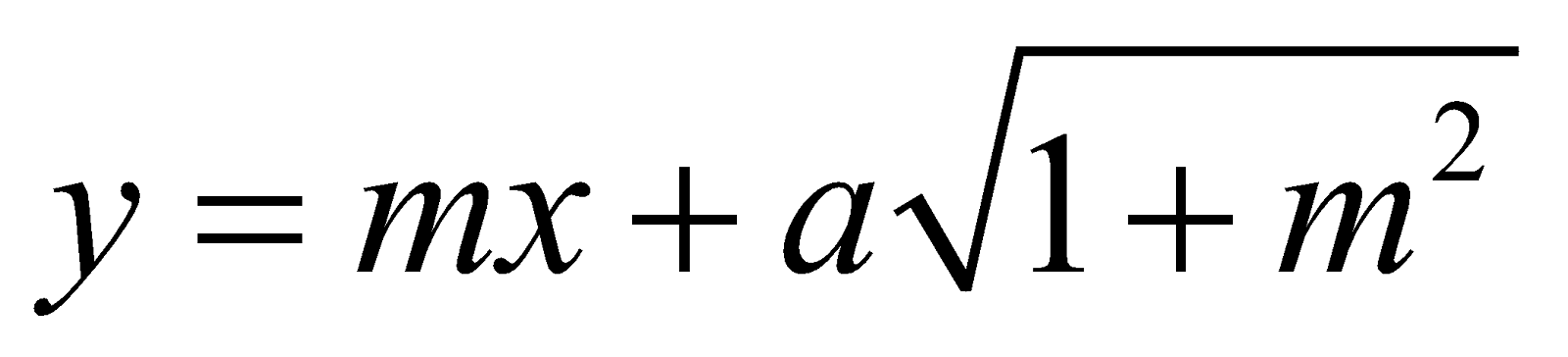be a tangent to the circle .

If it passes through a point P(x', y'), outside the circle, then

On squaring, we get

   ....(10)

IMPORTANT RESULTS

1. It is a quadratic in m hence, two tangents can be drawn from the point P to the circle.
2. If m1 and m2 be the roots of the equation (10) then and        ....(11)

The equation (11) provide the relations between the slopes of the two tangents.

3. If the tangents are perpendicular then m1m2 = –1, i.e.,
4. The locus of point P (x', y') under the condition m1m2 = –1 is therefore x2 + y2 = 2a2

Thus, the locus of point of intersection of the perpendicular tangents drawn to a circle is the circle given by x2 + y2 = 2a2. This is a circle concentric with the given circle and radius equal to × radius of given circle. This circle is called The DIRECTOR CIRCLE of the given circle.

5. The length of tangents to the circle from the point P is  
6. The length of tangents to the circle S (x, y) = from an external point
   P (x', y') is  or or .

POWER OF A POINT

If from a point P (x', y'), inside or outside the circle a secant be drawn intersecting the circle in two points A and B then PA.PB = Constant. The product PA.PB is called power of the point P.

That is for a number of secants

= PT2 = S(x′, y′)

Note :

1. If the two lines and  a2x + b2y + c2 = 0 meet the coordinate axes in four distinct points, then those points are concyclic if  (or the product of the slope = 1)

Also, the equation of the circle passing through those concyclic points is (a1x + b1y + c1)(a2x  + b2y + c2) – (a1b2 + a2b1) xy = 0 where a1a2 = b1 b2

2. The equation of the circumcircle of the triangle formed by the line ax + by + c = 0 with the coordinate axes is

PAIR OF TANGENTS

The equation of the pair of tangents drawn from the point
P(x1, y1) to the circle

S = 0 is SS1 = T2, where

and

Note :

The pair of tangents from (0,  0) to the circle x2 + y2 + 2gx + 2fy + c = 0 are at right angles if g2 + f2 = 2c

CHORD OF CONTACT OF TANGENTS

Let P be a point outside a circle. If two tangents PA and PB be drawn to the circle, then the chord AB is called the chord of contact of tangents drawn from the point P to the circle.

The equation of the chord of contact of tangents drawn from the point P (x1, y1) is given by

T = 0, i.e, xx1 + yy1 = a2 for the circle x2 + y2 = a2

and

for the circle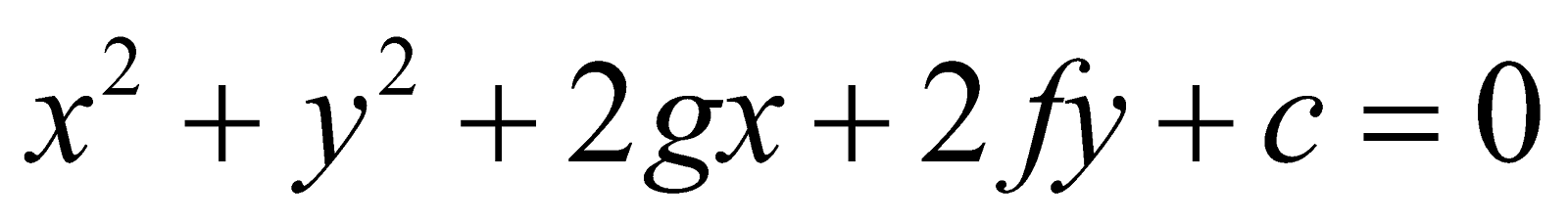

CHORD WITH A GIVEN MIDDLE POINT

The equation of the chord of the circle S = 0, whose middle point is (x1, y1), is given by T = S1. i.e.

+ 2gx1 + 2fy1 + c, for the circle and xx1 + yy1 – a2 = for the circle x2 + y2 = a2

Note :

1. If  (x1, y1) is the mid point of the chord PQ of the circle S = 0, then the length PQ = , where S1< 0
2. The coordinates of middle point of the chord lx + my + n = 0 of the circle x2  + y2 = a2 are
3. Let (x1, y1) be the mid point of the chord PQ of the circle S = 0. If the tangents at P and Q meet at R. then the area of where a is the radius of the circle.

CHORD OF CIRCLE JOINING TWO POINTS ON IT

Equation of the chord joining points and 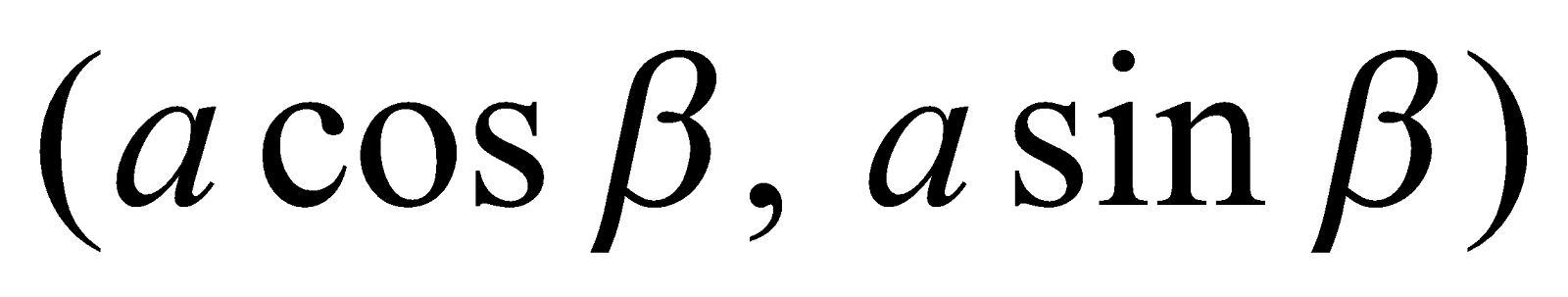on the circle is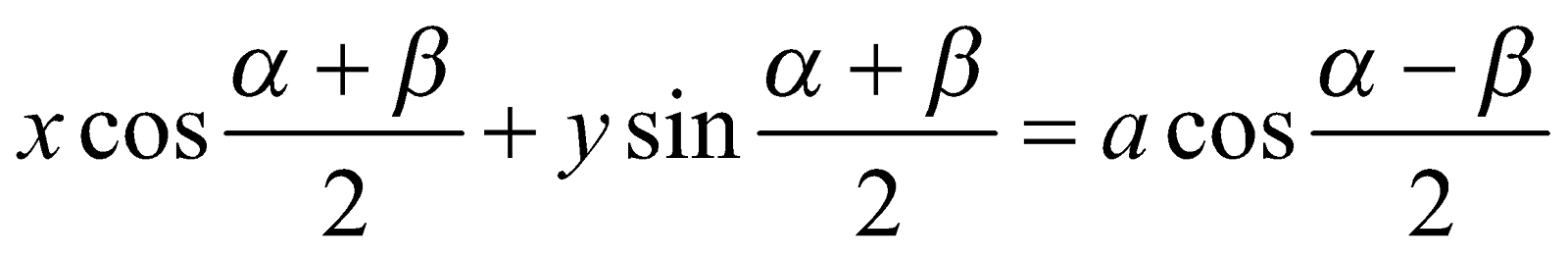

NORMAL TO A CIRCLE AT A GIVEN POINT

The normal to a circle at any point on the circle is a straight line which is perpendicular to the tangent to the circle at that point and always passes through the centre of the circle.

1. Equation of the normal to the circle at the point on it is :
2. Equation of the normal to the circle at the point (x1, y1) on it is

SYSTEM OF TWO CIRCLES

Consider two circles with centres C1 and C2 and radii r1 and r2.

Case I : If C2C2 > r1 + r2, i.e. the distance between centres > the sum of radii. Then the circles neither touch nor intersect and one circle is out of other

Case II : If C1C2 = r1 + r2. Then the circles touch one another externally and their point of contact has coordinates

       

Case III : If r2 – r1 < C1C2 < r1 + r2. Then the circles intersect in two distinct points. [Assuming r2 > r1].     

Case IV : If C1C2 = r2 – r1. Then the circle touch one another internally and their point of contact has coordinates

Case V : If C1C2 < r2 – r1. Then the smaller circle completely lies inside the bigger circle.

Note :

• The condition that the two circles touch is C1C2 = r2 ± r1 (Assuming r2 > r1)
• If C1C2 = r2 – r1, we may, alternatively state that one of the circles is just sufficient in size to contain the other circle.

COMMON TANGENTS TO TWO CIRCLES

DIRECT COMMON TANGENTS

The direct Common tangents to the two circles meet at a point (say P) which lies on the line joining the centres C1 and C2 of the two circles and divide C1C2 externally in the ratio of their radii say (r1 and r2).

WORKING RULE

1. Find the coordinates of centre C1, C2 and radii r1, r2 of two given circles.
2. Find the coordinates of the point P dividing C1C2 in the ratio externally.
   Let
3. Write the equation of any line through the point P (h, k), i.e.
   ...(1)
4. Find the two values of m, using the fact that the length of perpendicular on line (1) from the centre C1 of one circle is equal to its radius r1.
5. Substituting these values of m in equation (1), the equations of two direct common tangents are obtained.

TRANSVERSE COMMON TANGENTS

The transverse common tangents to the two circles intersect at a point (say Q) which lies on the line joining the centres C1and C2 of the two circles and divide C1C2 internally in the ratio of their radii r1 and r2

WORKING RULE

1. Find the coordinates of centres C1, C2 and radii r1, r2 of two given circles.
2. Find the coordinates of the point Q dividing C1C2, in the ratio r1 ; r2 internally. Let
3. Write the equation of any line through the point P (h, k) i.e.,
4. Find the two values of m, using the fact that the length of perpendicular on (1) from the centre C1 of one circle is equal to its radius r1
5. Substituting these values of m in equation (1), the equations of two transverse common tangents are obtained.

Remark :

1. If two circles do not intersect then they have two transverse and two direct common tangents.
2. If two circles intersect (| r1 – r2 | < C1C2 < r1 + r2) then they have two direct tangents only
3. If two circles touch externally (C1C2 = r1 + r2), then they have one transverse and two direct common tangents
4. If two circles touch internally (C1C2 = | r1 – r2 |) then they have only one common tangent.
5. If one circle lies inside the other (C1C2 < |r1 – r2|, then they have no common tangent.

CASE OF INTERSECTING CIRCLES

If | r2 – r1 | < C1C2 < r1 + r2

Then the two circles intersect in two real and distinct points.

Let the equations of the circles be

        S1 :  

and   S2 :  

The line joining the points of intersection A and B is called the common chord of two circles.

The equation of the common chord is given by  S2 – S1 = 0, that is  ...(1)

The length of the common chord is given by

where C2A is radius of the second circle and C2M is the length of perpendicular from the centre of the second circle to the common chord given by equation (1).

IMPORTANT NOTE

1. The length of the common chord is maximum when it is a diameter of the circle of smaller radius.
2. If the length of common chord is zero, then the two circles touch each other and the common chord becomes the common tangent to the two circles at the common point of contact.
3. If a circle bisects the circumference of another circle then the common chord of two circles becomes a diameter of the second circle.

ANGLE THE INTERSECTION OF TWO CIRCLES

The angle of intersection of two circles (or any two curves) is the angle between the tangents to two circles at the common point.

If m1 and m2 be the slopes of the tangents drawn to the circles at the common point then then angle of intersection of the circles 'θ' is given by

Since the angle between the tangents to two circles and the angle between the normals to two circles at the point of intersection are supplementary, we can write the angle of intersection using cosine rule. So,

If θ=π/2 , the circles are said to be ORTHOGONAL CIRCLES. The circles given by the general equations S1 = 0 and S2 = 0 are orthogonal if

RADICAL AXIS OF TWO CIRCLES

The locus of point from which the tangents of equal lengths can be drawn to two circles is a straight line called as RADICAL AXIS of the circles.

    

Remark :

1. The equation of Radial axis  is given by S2 – S1 = 0, hence it is identical to the equation (1) of common chord.
2. If the circles touch, the common tangent at the point of contact of the circles is the Radical axis.
3. If the circles intersect the Radical axis is simply the extension of common chord.
4. The line joining centres C1C2 is perpendicular to the radical axis (common chord).

PROPERTIES OF RADICALS

1. Radical Centre : The radical axis of three circles taken in pairs meet at a point, called the radical centre of the circles. Coordinates of radical centre can be found by solving the equations S1 = S2 = S3 = 0
2. The radical centre of three circles described on the sides of triangle as diameters is the orthocentre of the triangle.
3. If two circles cut a third circle orthogonally, then the radical axis of the two circles will pass through the centre of the third circle.
4. The circle having centre at the radical centre and radius equal to the length of tangent from radical centre to any of the circles, intersects all the three circles orthogonally.

COAXIAL SYSTEM OF CIRCLES

A system of circles is said to be coaxal if each pair of circles of the system has the same radical axis

EQUATION OF THE SYSTEM OF COAXIAL CIRCLES IN THE SIMPLEST FORM

The equation of a system of coaxial circles is

where g is a constant and c is a parameter and the line of centre of the circles is taken as x-axis and the radical axis as the y-axis.

Note :

1. The equation of a system of coaxial circles, when the equation of the radical axis and one circle of the system are and  
1. respectively, is S + λP = 0 (λ is an arbitrary constant)
2. The equation of a coaxial system of circles when the equation of any two circles of the system are

and is S1 + λ (S1 – S2) = 0

or S2 + λ (S1 – S2) = 0    i.e. S1 + λS2 = 0 (λ ≠ –1)

LIMITING POINTS OF A COAXIAL SYSTEM

Limiting points of coaxial system of circles, are point circles of the system i.e circles of radius zero. The limiting points of the system of circles

are .

Obviously limiting points are real only if .

FAMILY OF CIRCLES

1. The equation of circles CONCENTRIC with a given circle

is ...(1)

where λ may be determined from given conditions.

2. The equation of circles through the points of intersection of a circle

S = 0 and a straight line L = 0 is given by

S + λL = 0 ...(2)

3. The equation of circles through the points of intersection of two circles S1 = 0 and S2 = 0 is given by
   

S1 + λS2 = 0 or S1 + λ (S2 – S1) = 0 ...(3)

where λ may be determined from given conditions.

4. Equation of family of circles touching a straight line L = 0, at a point (x1, y1) is λ is parameter
5. Equation of family of circles through two distinct points (x1, y1) and (x2, y2) is (x – x1) (x – x2) + (y – y1) (y – y1) + λL = 0, λ is parameter.

Where L = 0 is the equation of the line through (x1, y1) and (x2, y2).  

Alternatively we can write

Mathematics Study Notes

• Sets, Relations and Functions
• Trigonometric Ratios and Identities
• Trigonometric Equations and Inequations
• Properties of Triangles, Height and Distances
• Principle of Mathematical Induction, Permutation and Combination
• Complex Numbers
• Quadratic Equations
• Linear Inequalities
• Sequences and Series
• Binomial Theorem
• Infinite Series
• Points & Straight Lines
• Pair of Straight Lines
• Circles
• Parabola
• Ellipse and Hyperbola
• Mathematical Reasoning
• Statistics
• Probability Basic
• Functions
• Inverse Trigonometric Functions
• Matrices
• Determinants
• Limits, Continuity and Differentiability
• Differentiation and Application of Derivatives
• Indefinite Integration
• Definite Integration and Applications
• Differential Equations
• Vector Algebra
• Three Dimensional Geometry
• Probability Advanced

Study Notes for JEE Main/JEE Advanced/BITSAT