DEFINITE INTEGRATION & APPLICATIONS
INTRODUCTION
Let f(x) be a function defined on the interval [a, b] and F(x) be its antiderivative. Then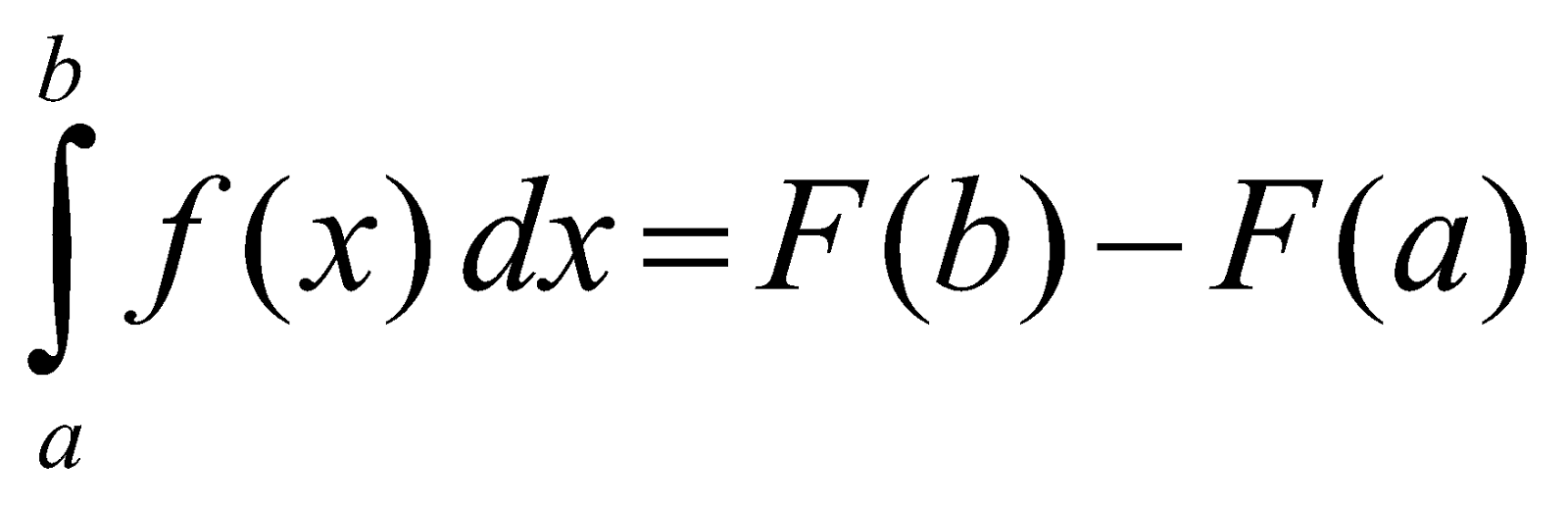 
The above is called the second Fundamental Theorem of calculus.
is defined as the definite integral of f(x) from x = a to x = b.
The numbers a and b are called limits of integration. We write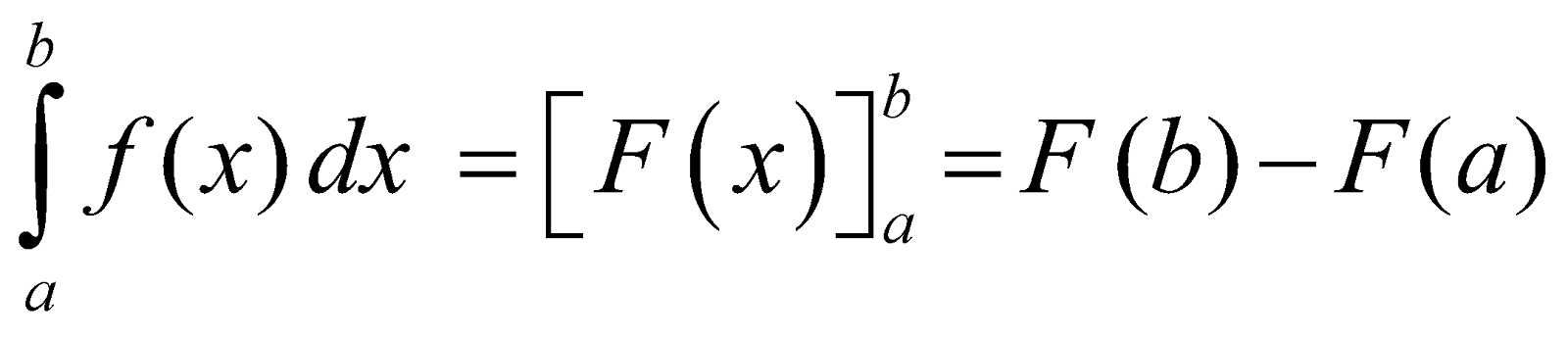
EVALUATION OF DEFINITE INTEGRALS BY SUBSTITUTION
Consider a definite integral of the following form
To evaluate this integral we proceed as following
Step 1 : Substitute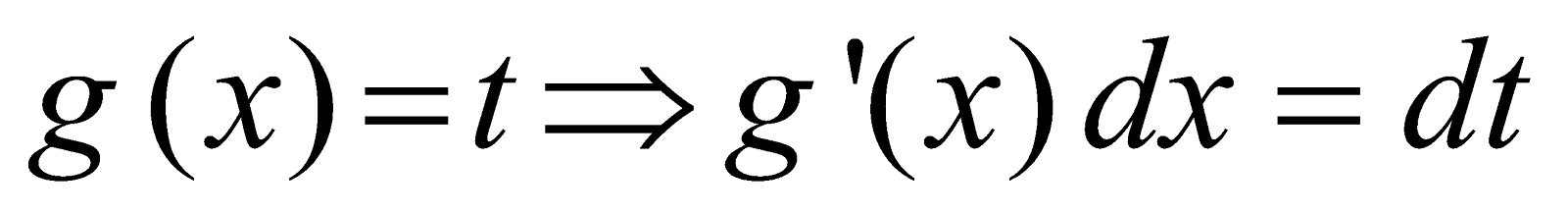 
Step 2 : Find the limits of integration in new system of variable, i.e. the lower limit is g(a) and the upper limit is g(b), and the integral is now 
Step 3 : Evaluate the integral so obtained by usual method.
FUNDAMENTAL PROPERTIES OF DEFINITE INTEGRALS
PROPERTY 1
The definite integral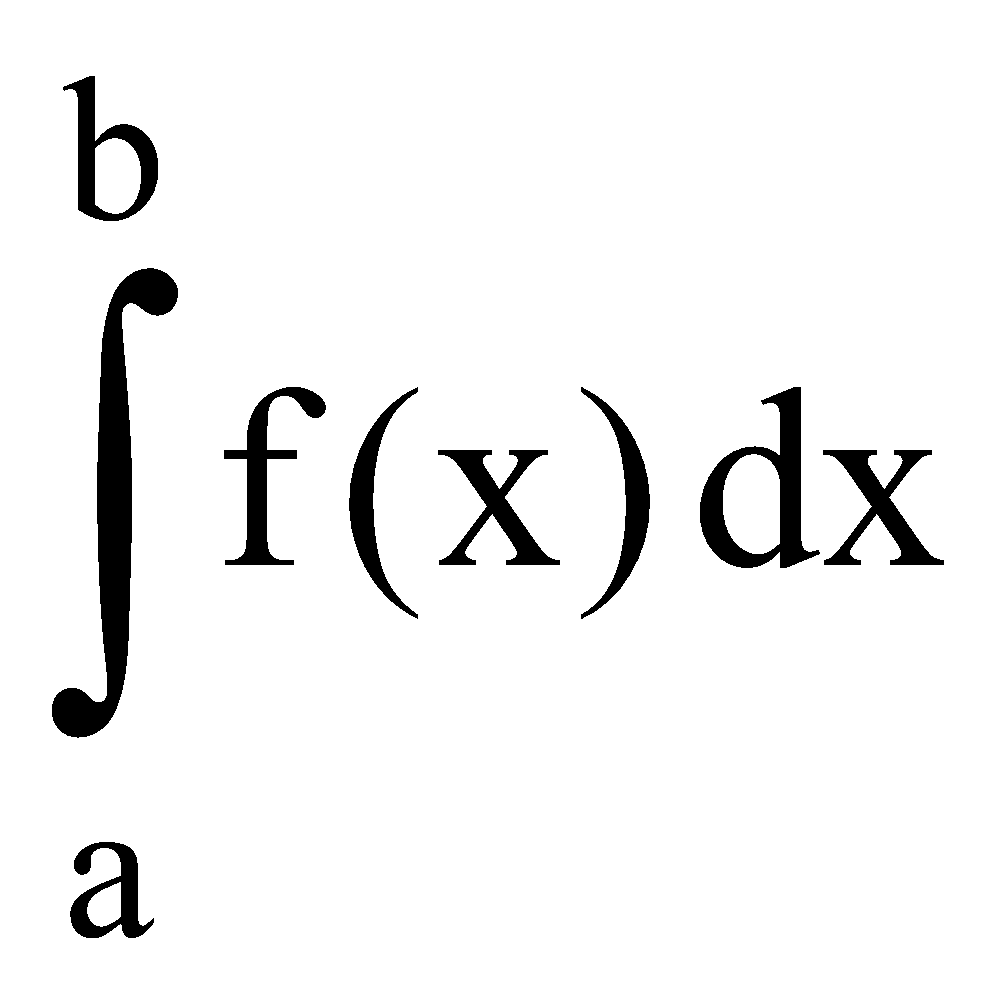
is a unique number.
is a unique number.
[Note that the indefinite integral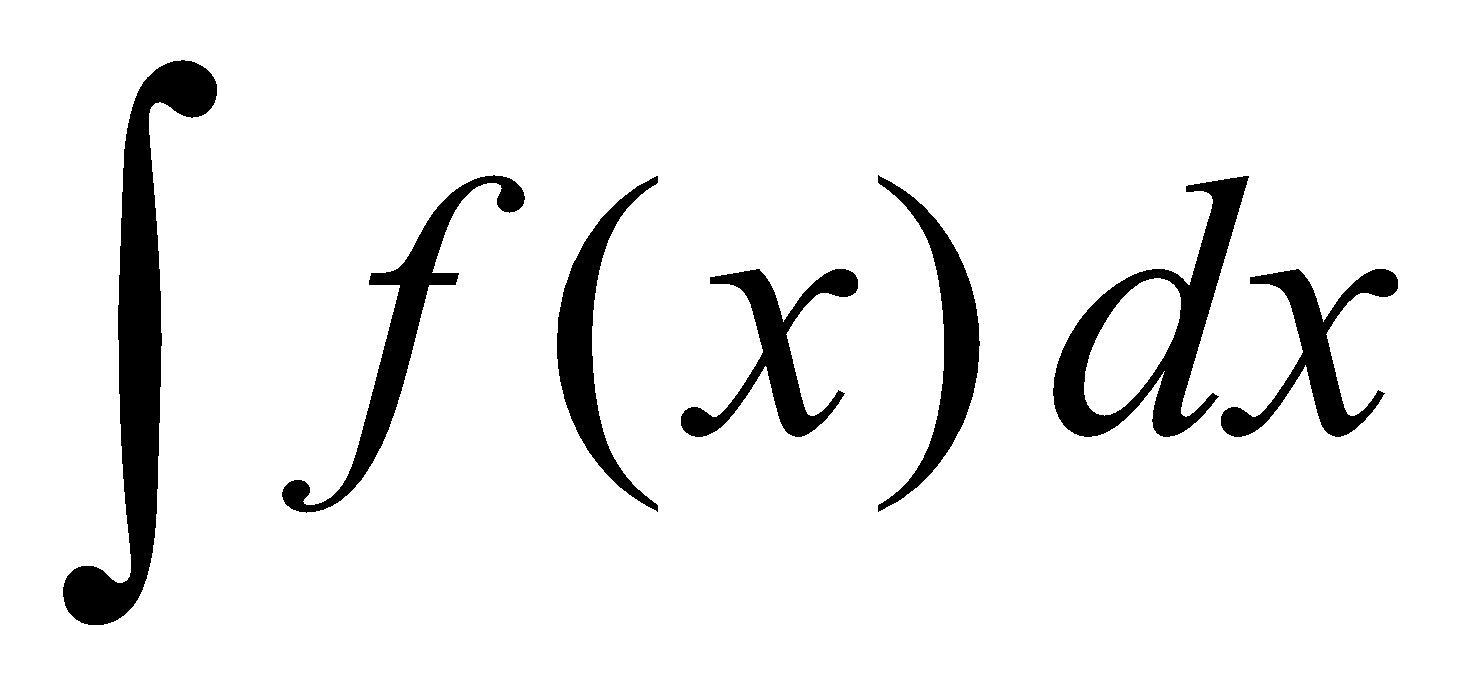 
is not unique]
is not unique]PROPERTY 2
The definite integral is independent of the change of variable. thus,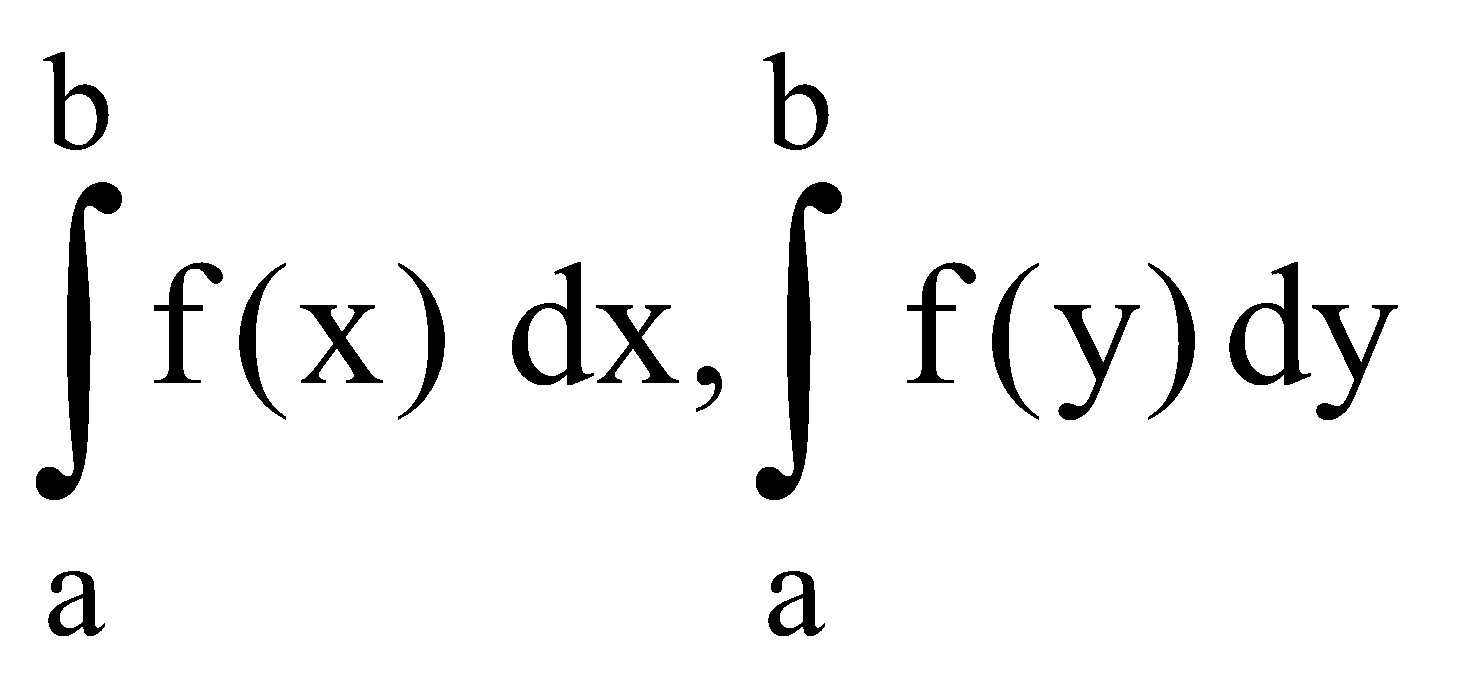 
etc all denote the same quantity.
etc all denote the same quantity.PROPERTY 3
If the limits of definite integral are interchanged then its value changes sign, that is
PROPERTY 4
If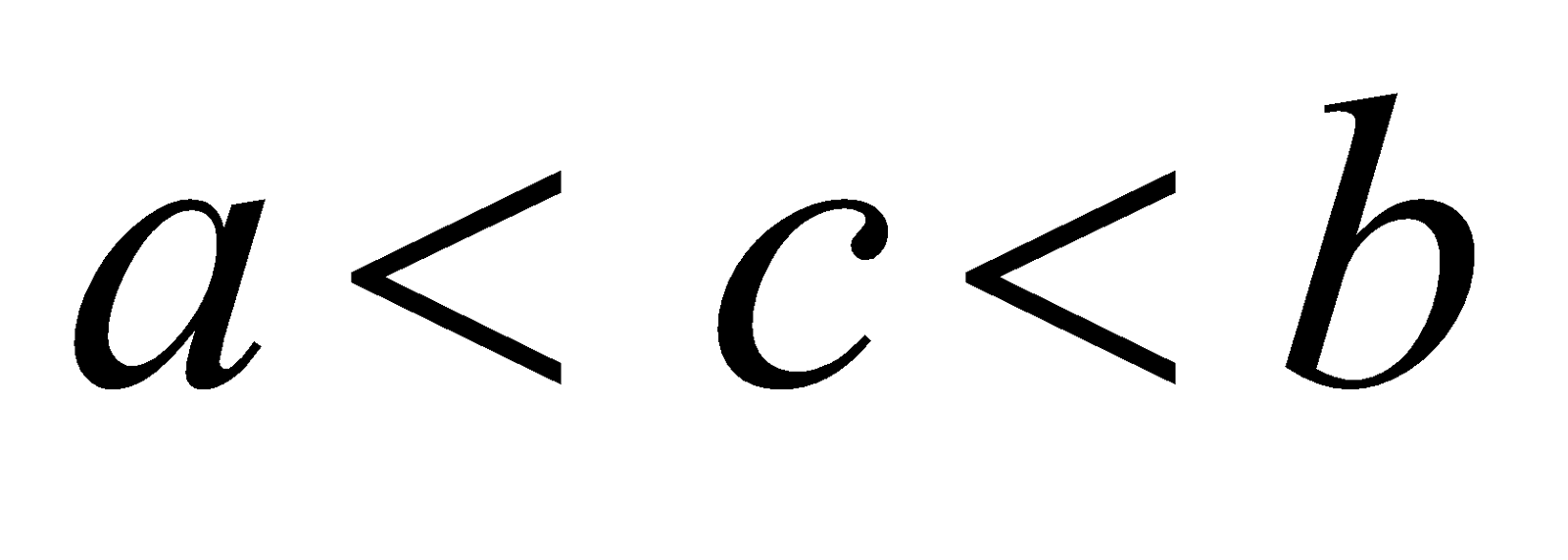 
then
then 
GENERALIZATION
If a < c1 < c2 < ........... < cn–1 < cn < b then
The property 4 is very useful in solving the integrals of functions defined in steps or modulus function or greatest integer functions.
PROPERTY 5
PROPERTY 6
This is very important property, because using this property many definite integrals can be evaluated without first finding the corresponding indefinite integrals which may be difficult or sometimes impossible to find.
DEDUCTION
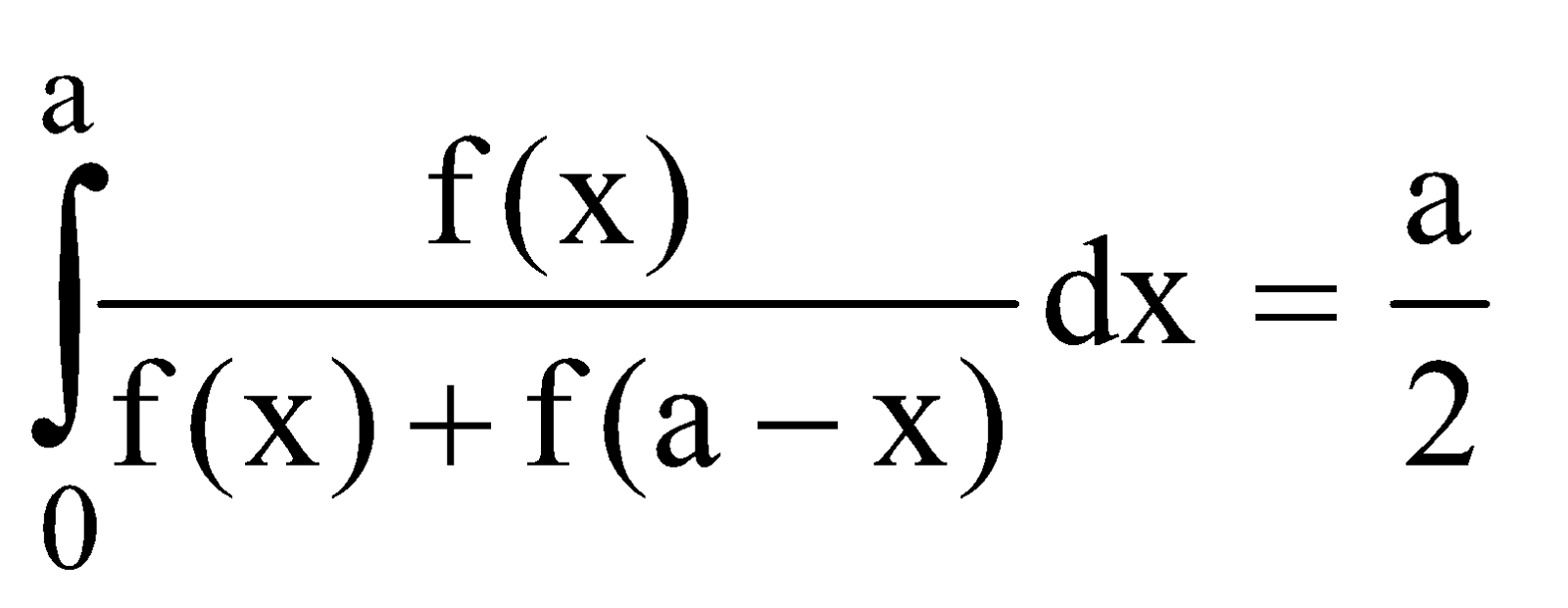
Let I =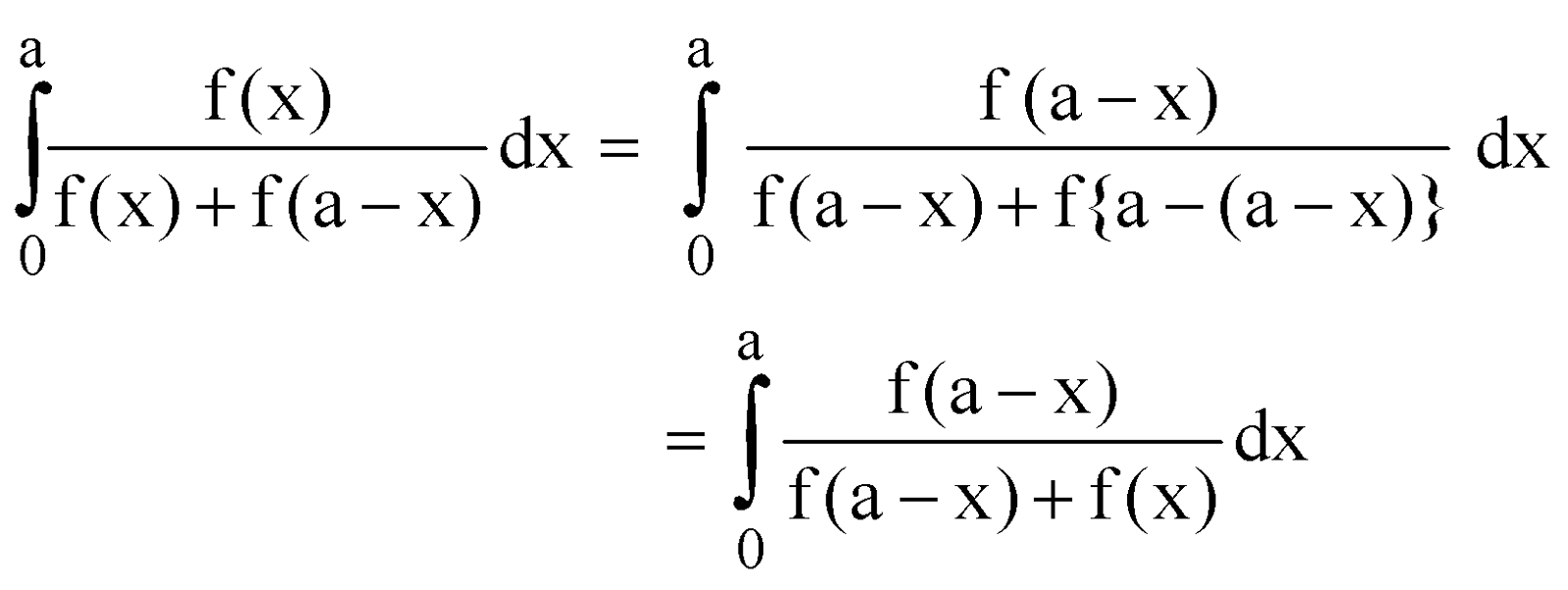 
=
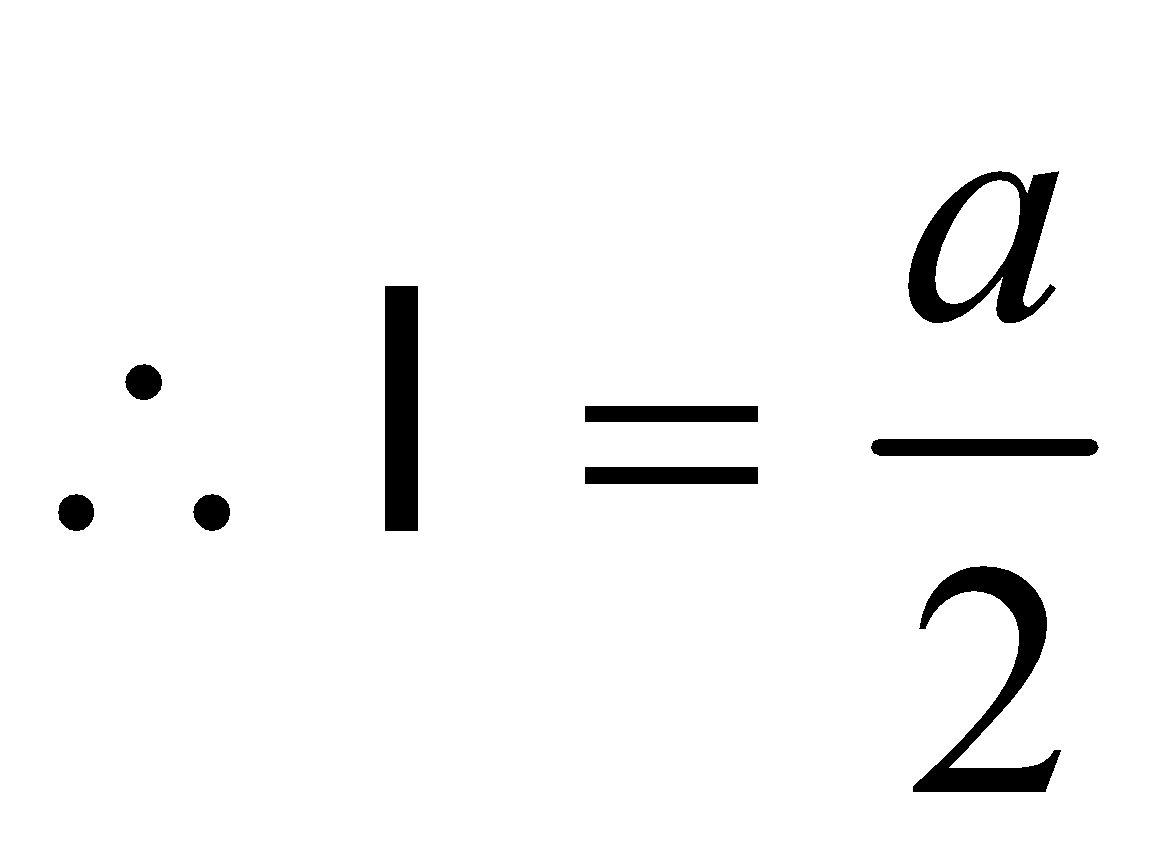
Example :
PROPERTY 7
DEDUCTION
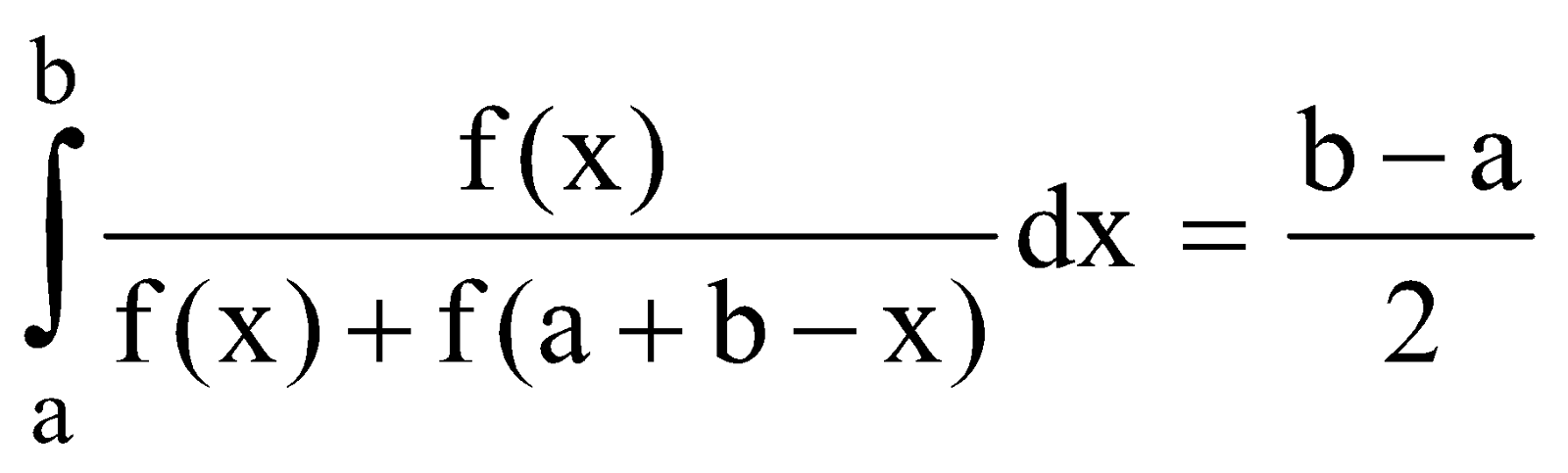
Let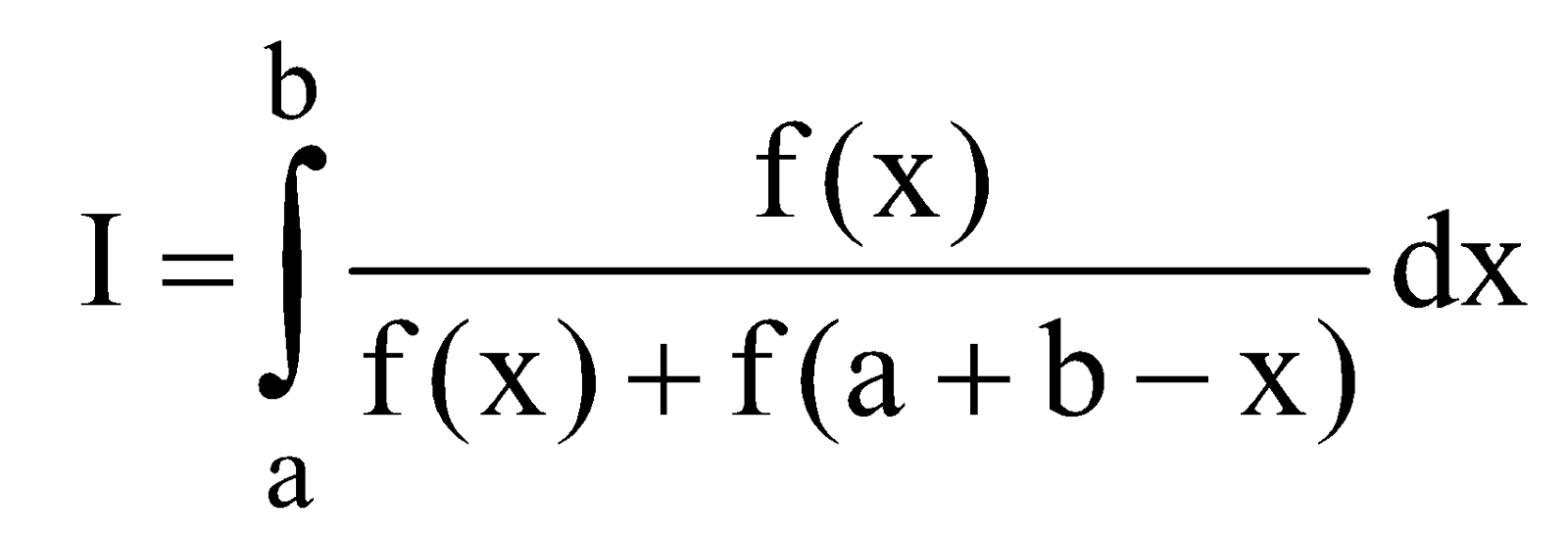
Example :
PROPERTY 8
DEDUCTION
Example 1 : Evaluate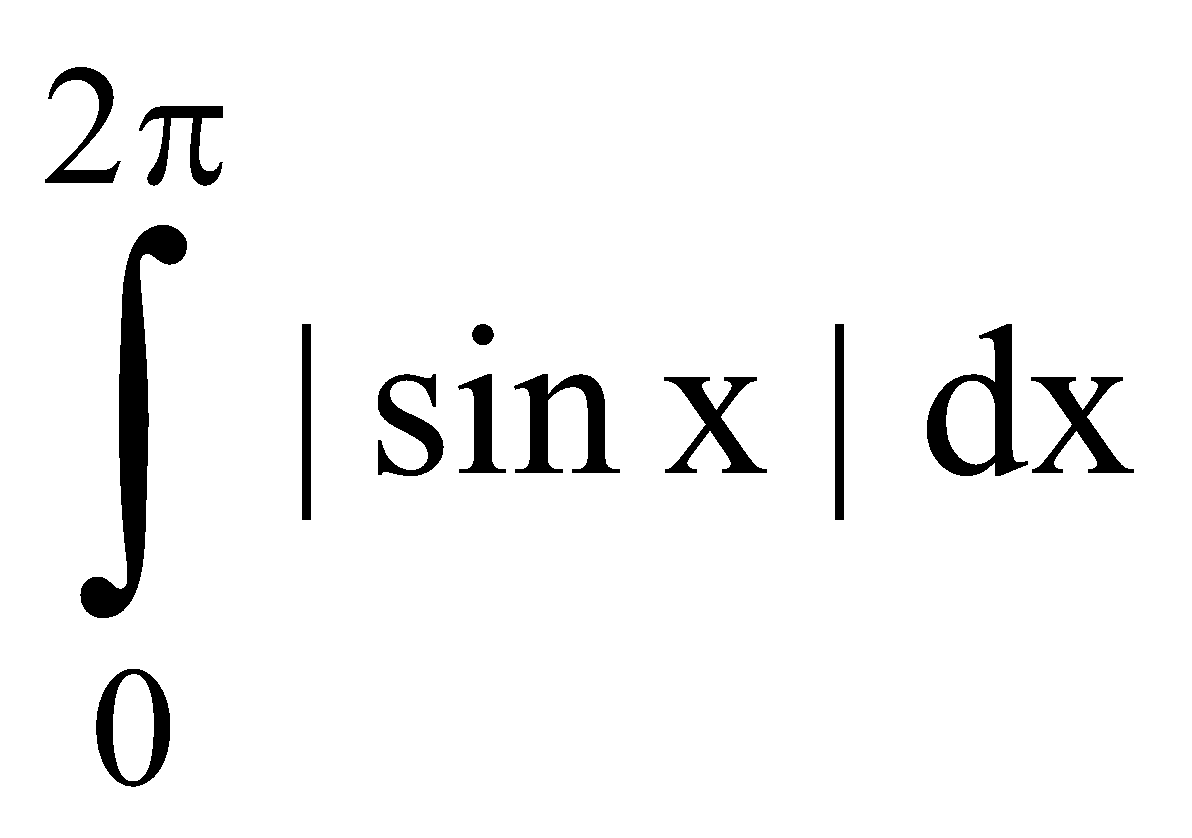 
Example 2 :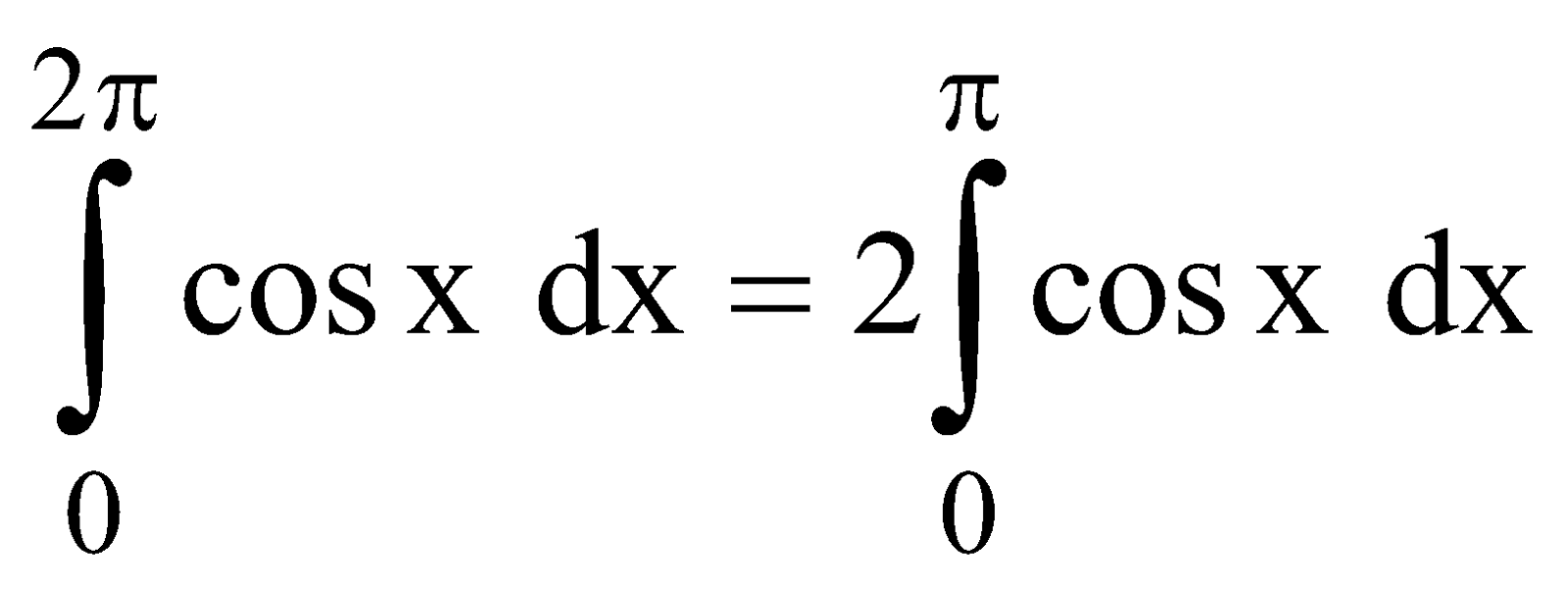 
As cos (2Ï€ – x) = cosx
As cos (2Ï€ – x) = cosx
= 0 As cos (Ï€ – x) = –cosx
In general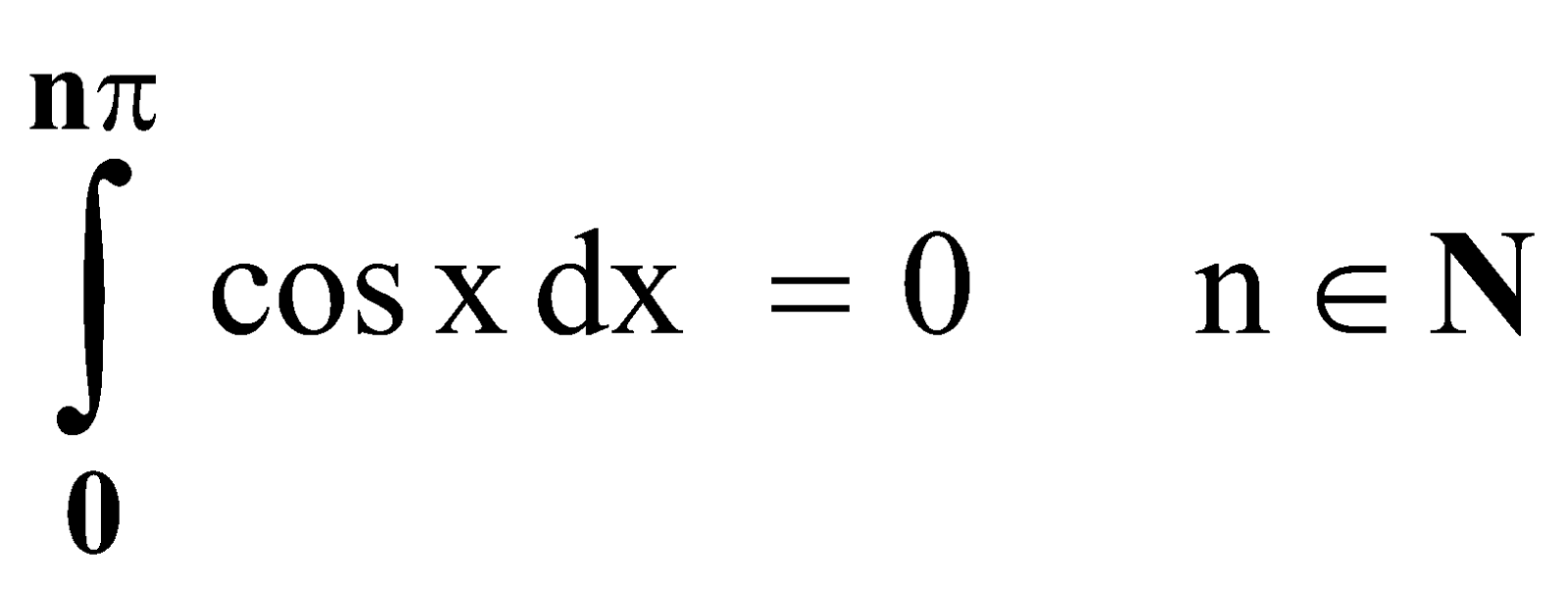 
PROPERTY 9
DEDUCTION
- If
- If
Example 1 : Evaluate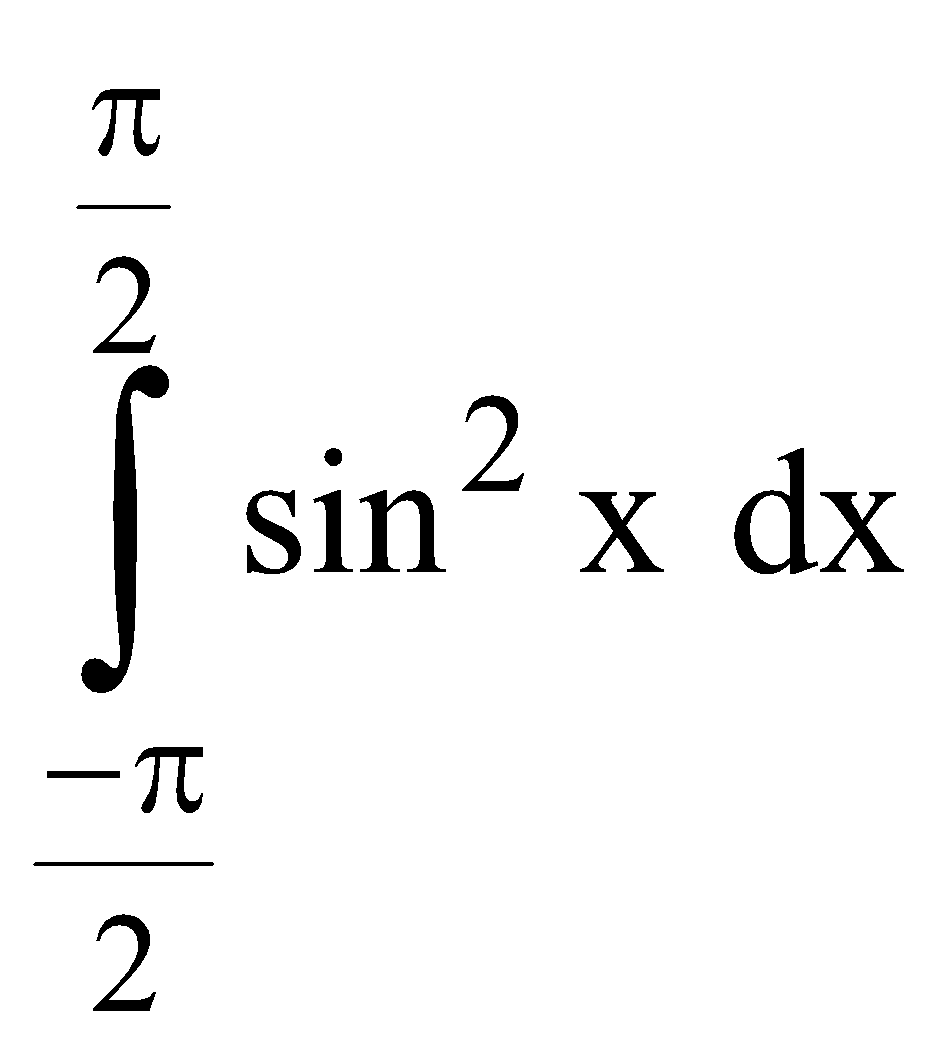 
Here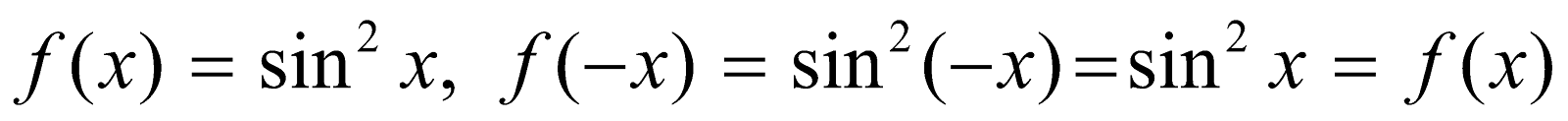 
Example 2 : I =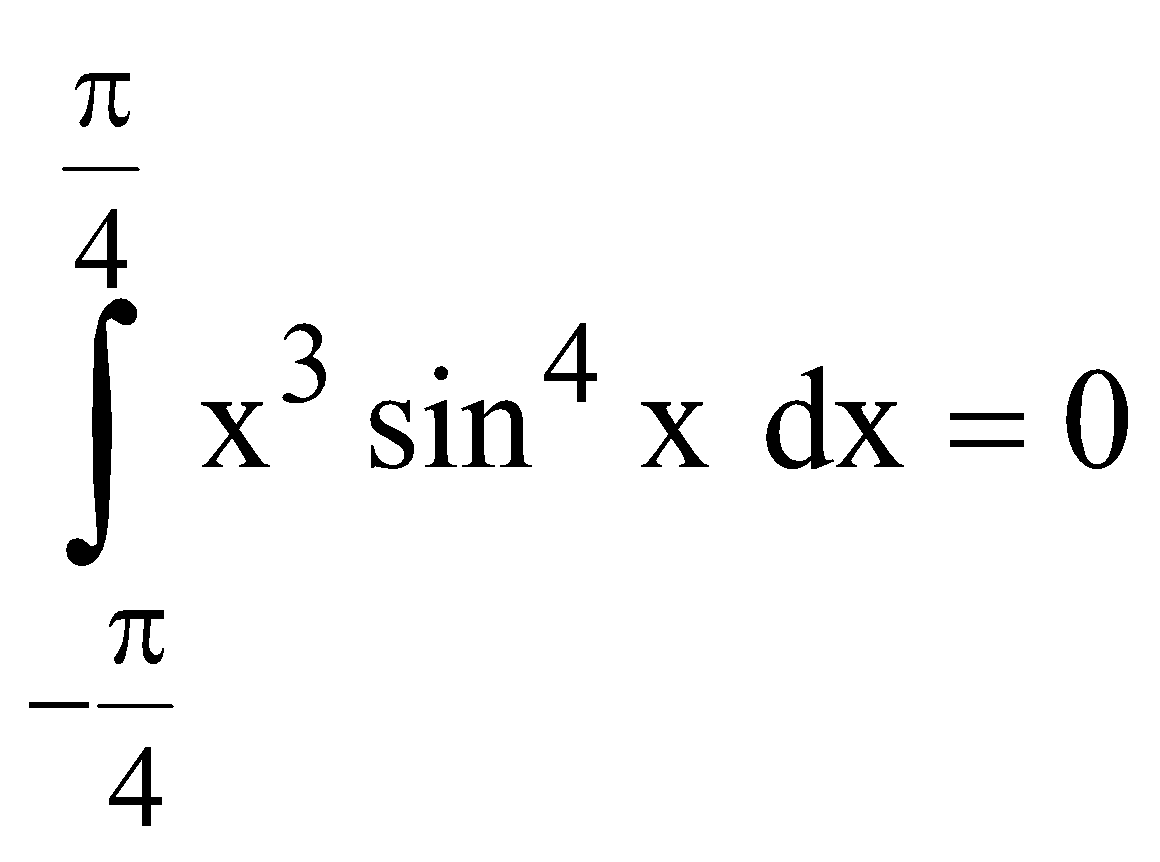
for 
is an odd function
for 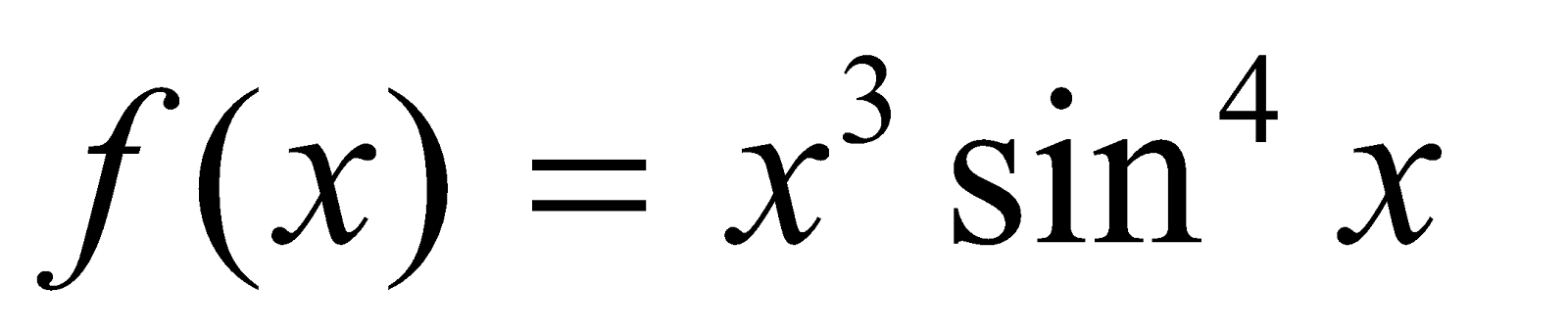is an odd functionPROPERTY 10
If f(x) is periodic function with period T,
[i.e. f(x + T) = f(x)] Then
[i.e. f(x + T) = f(x)] Then
(i)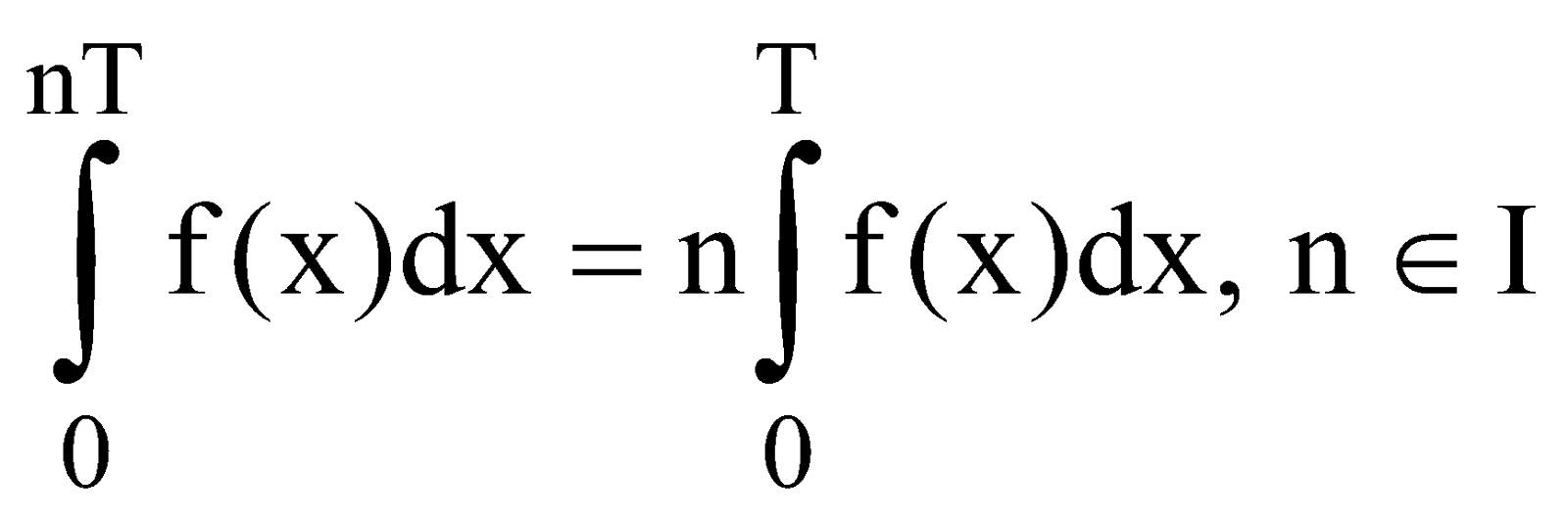 
(ii) 
(iii)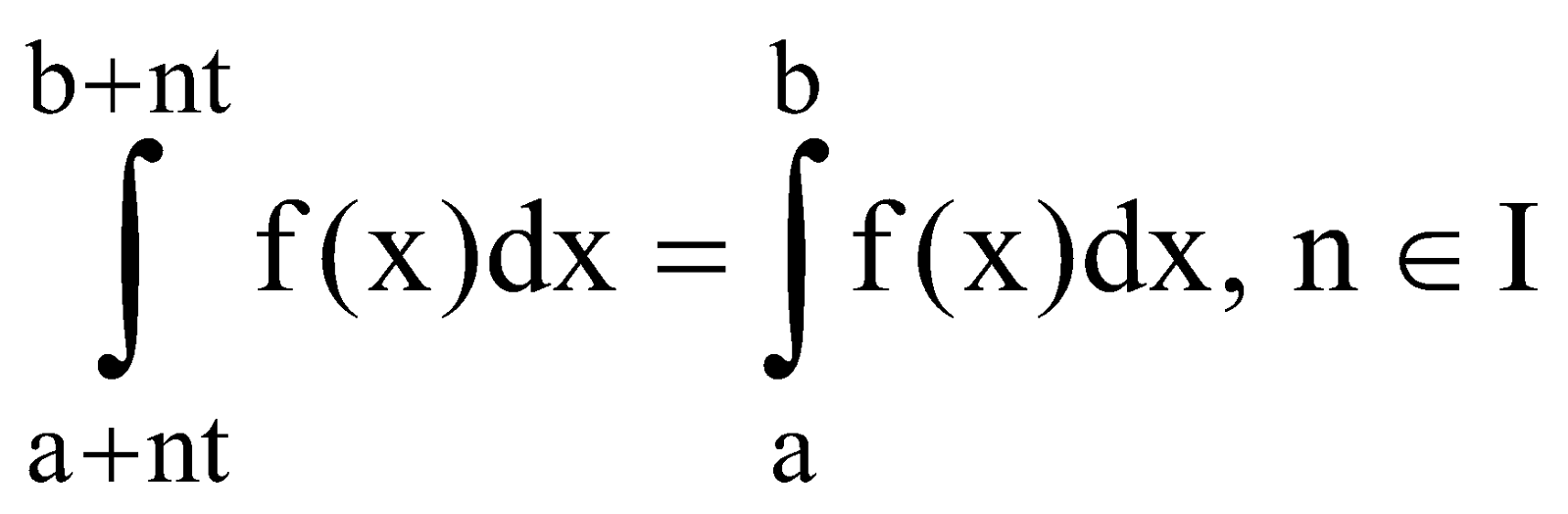 
Example 1 :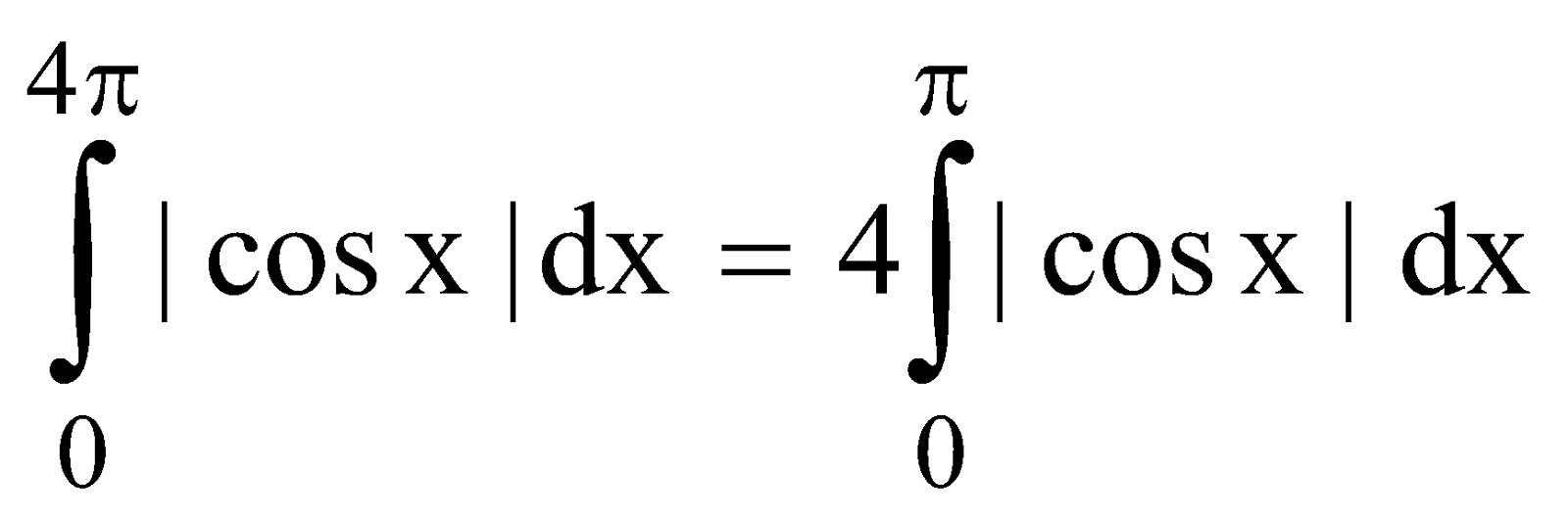 
[since |cos x| is a periodic function with period π]
PROPERTY 11 - LEIBNITZ RULE FOR DIFFERENTIATION UNDER INTEGRAL SIGN
If φ (x) and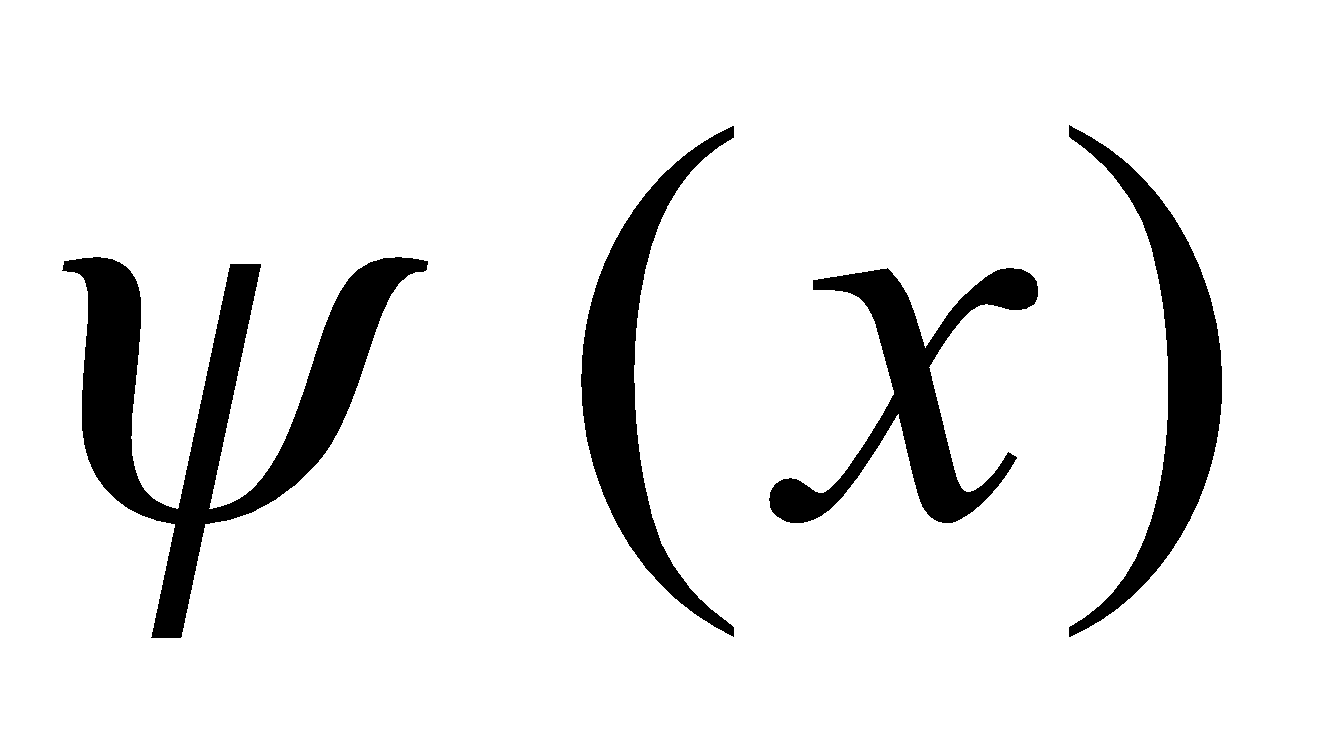
are defined over [a b] and differentiable for every x and f(t) is continuous, then
are defined over [a b] and differentiable for every x and f(t) is continuous, then
Example : Find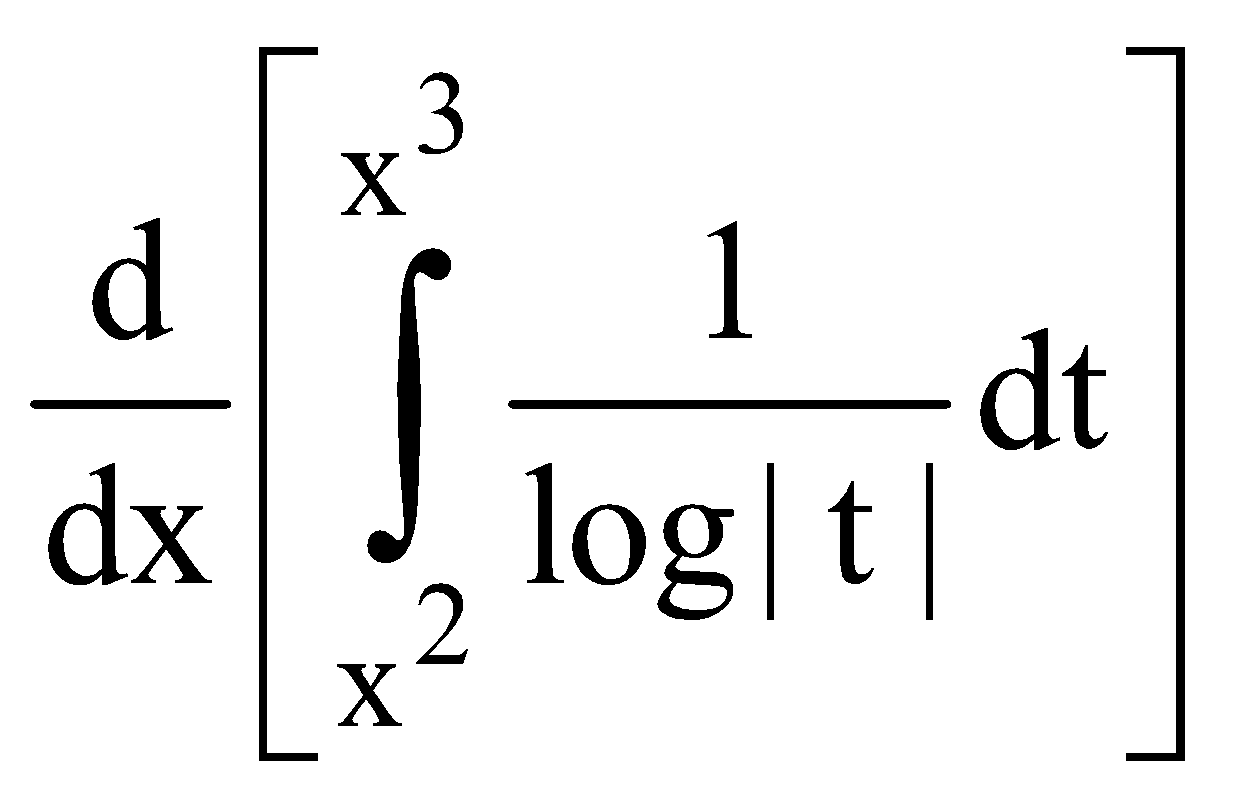 
GEOMETRICAL INTERPRETATION OF DEFINITE INTEGRALS
The definite integral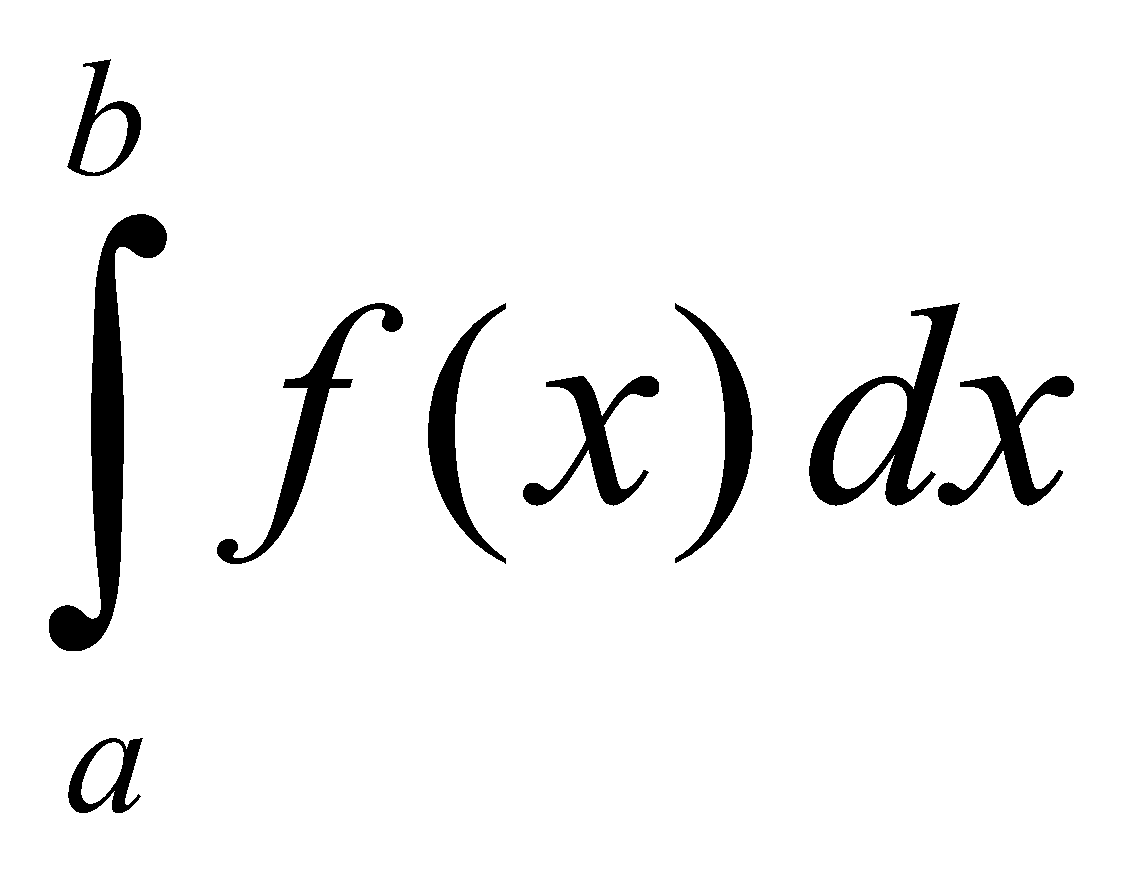 
is numerically equal to the area bounded by the curve y = f (x), the x-axis and the ordinates x = a, and x = b, as shown by shaded region in the adjacent figure
is numerically equal to the area bounded by the curve y = f (x), the x-axis and the ordinates x = a, and x = b, as shown by shaded region in the adjacent figure
AREA FUNCTION
Consider the definite integral
.
.
It represents the area of the shaded region shown in the adjacent figure.
The area of this shaded region is a function of x. Let us denote this function by A(x). We call this function A(x) as area function A (x) =
.
.
Note : The area function can be used to obtain indefinite integral of f(x) if we know the definite integral.
FIRST FUNDAMENTAL THEOREM OF CALCULUS
Let the area function be defined by A (x) =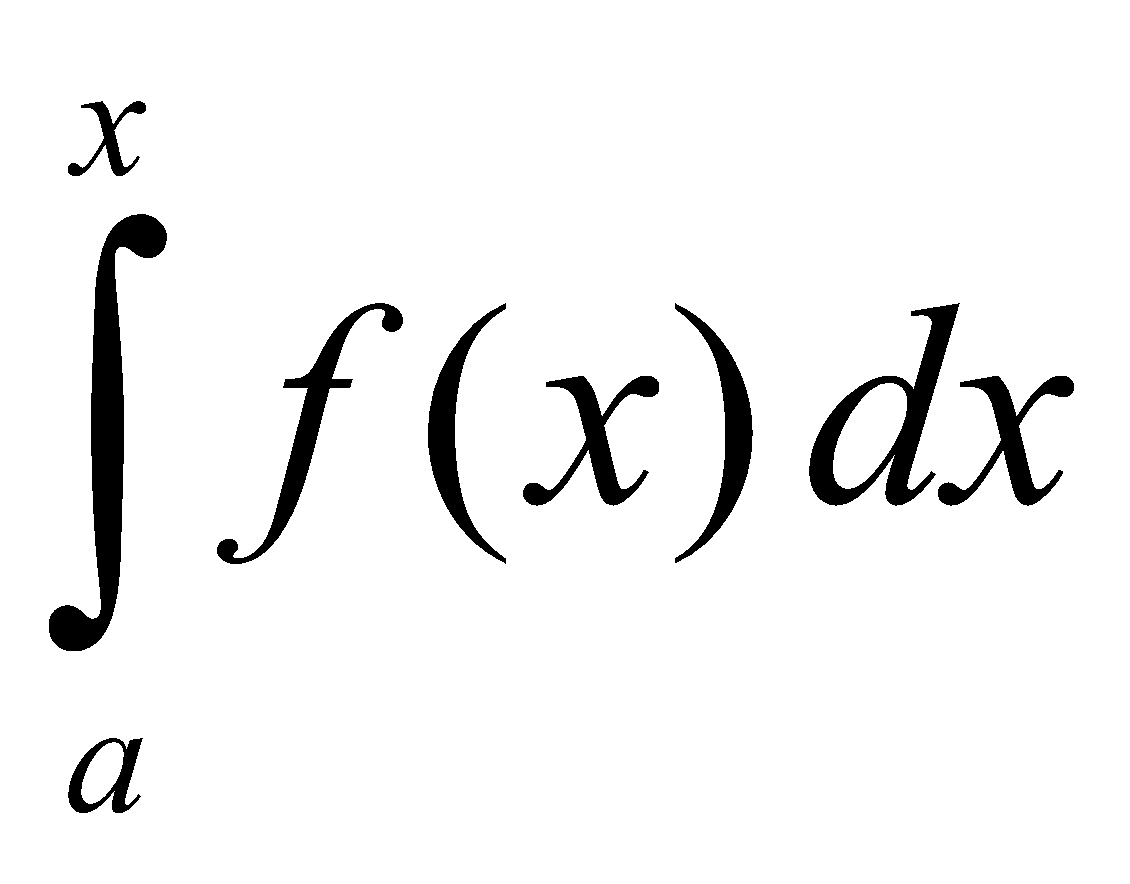
for all x ≥ a. Then A’(x) = f (x)
for all x ≥ a. Then A’(x) = f (x)DEFINITE INTEGRAL AS LIMIT OF A SUM
The definite integral 
can also be expressed as a limiting case of summation of an infinite series, provided f(x) is continuous on [a b]. We define
can also be expressed as a limiting case of summation of an infinite series, provided f(x) is continuous on [a b]. We define
,
In particular if a = 0 and b = 1,
we get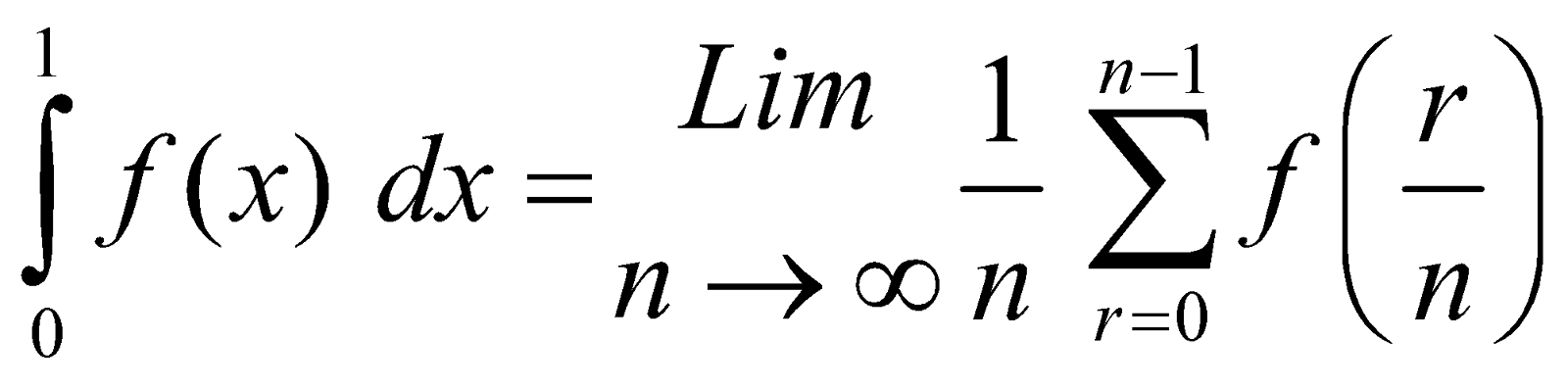 
WORKING RULE
If a given series is expressible in the form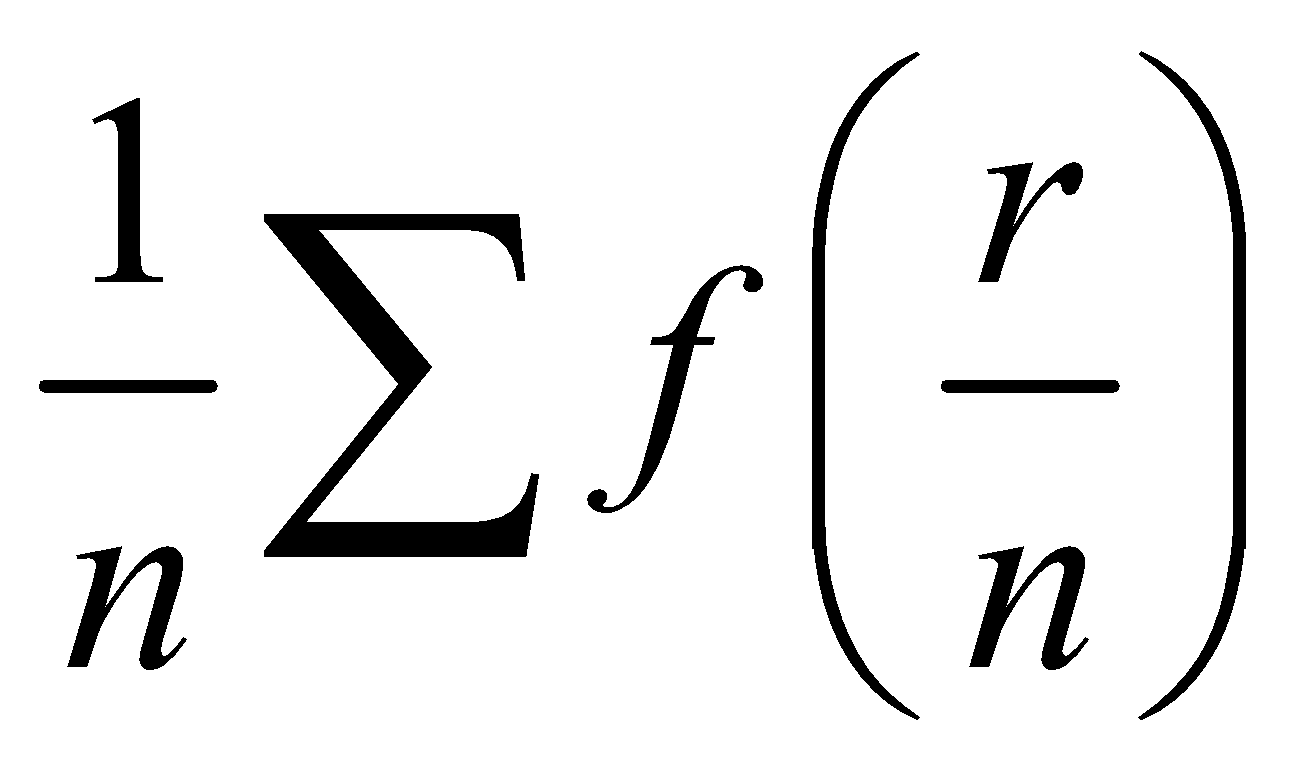
, then its limit as
can be expressed as a definite integral by writing x for 
, dx for 
and integral sign 
. The lower and upper limits of integration are the values of 
for the least and the greatest values of r respectively. In general
, then its limit as can be expressed as a definite integral by writing x for 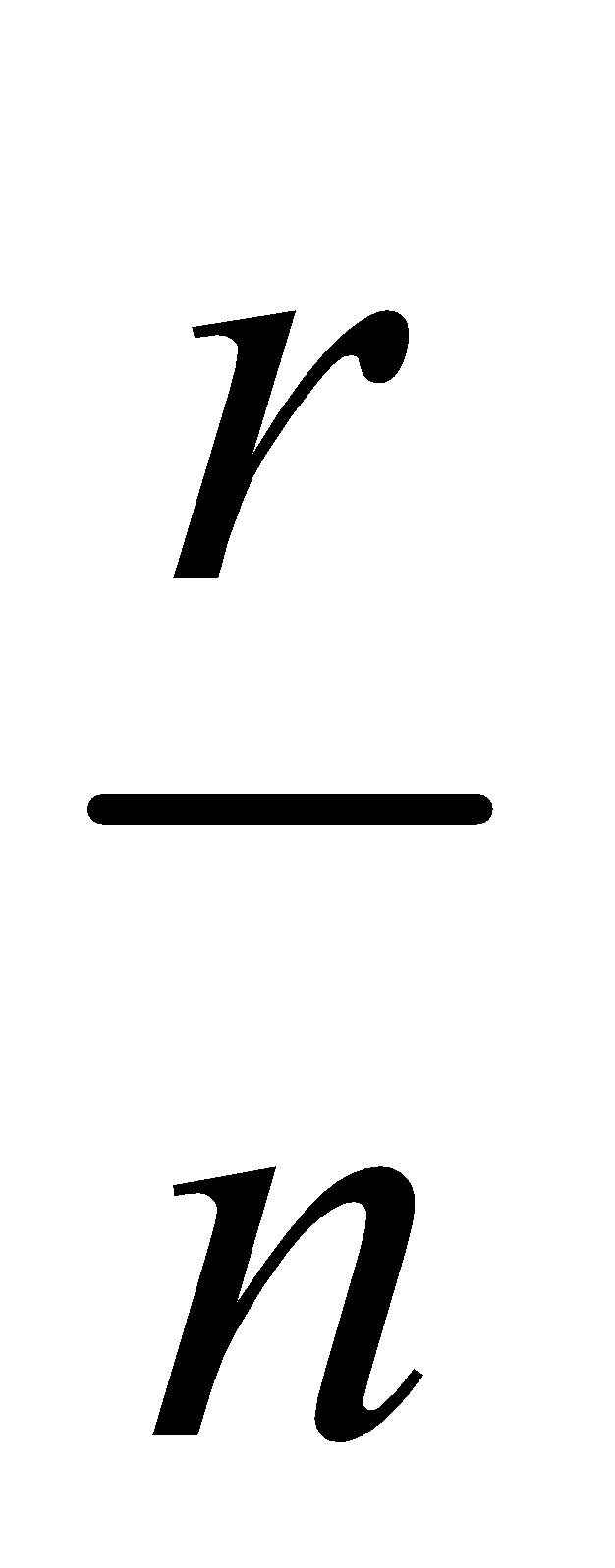, dx for 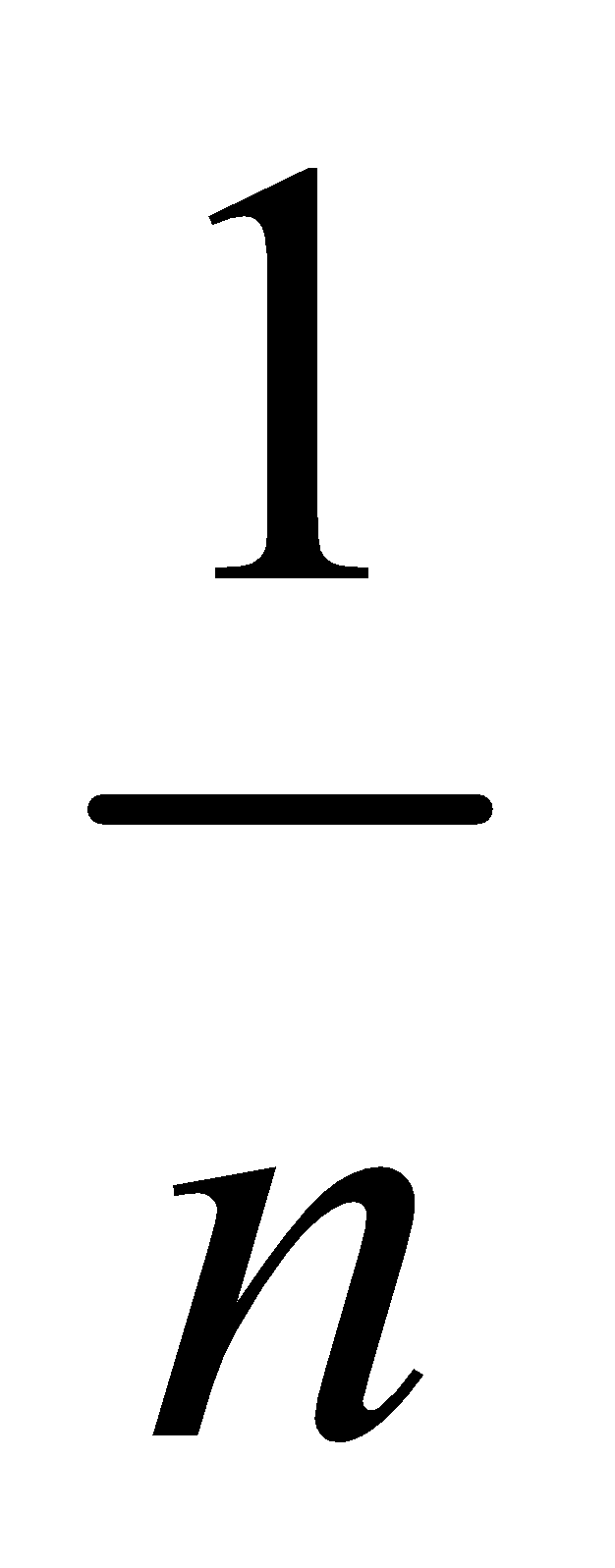and integral sign 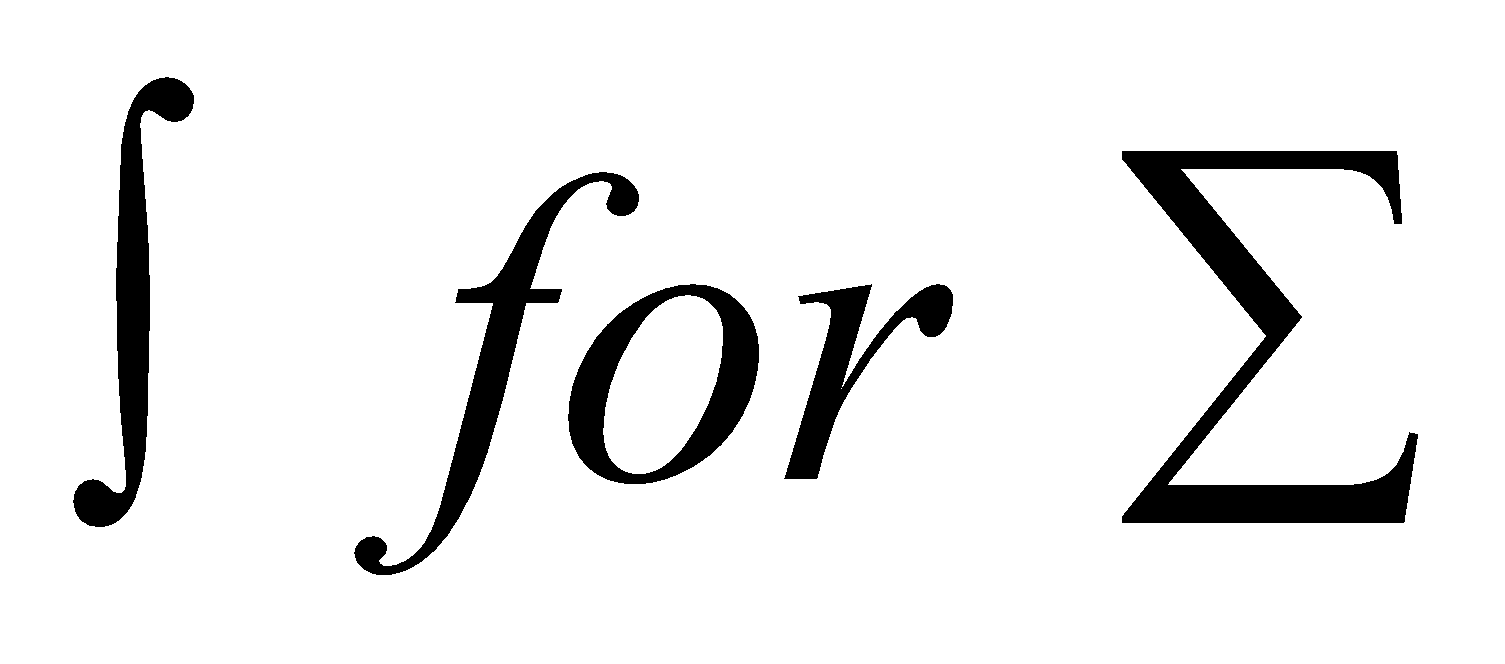. The lower and upper limits of integration are the values of 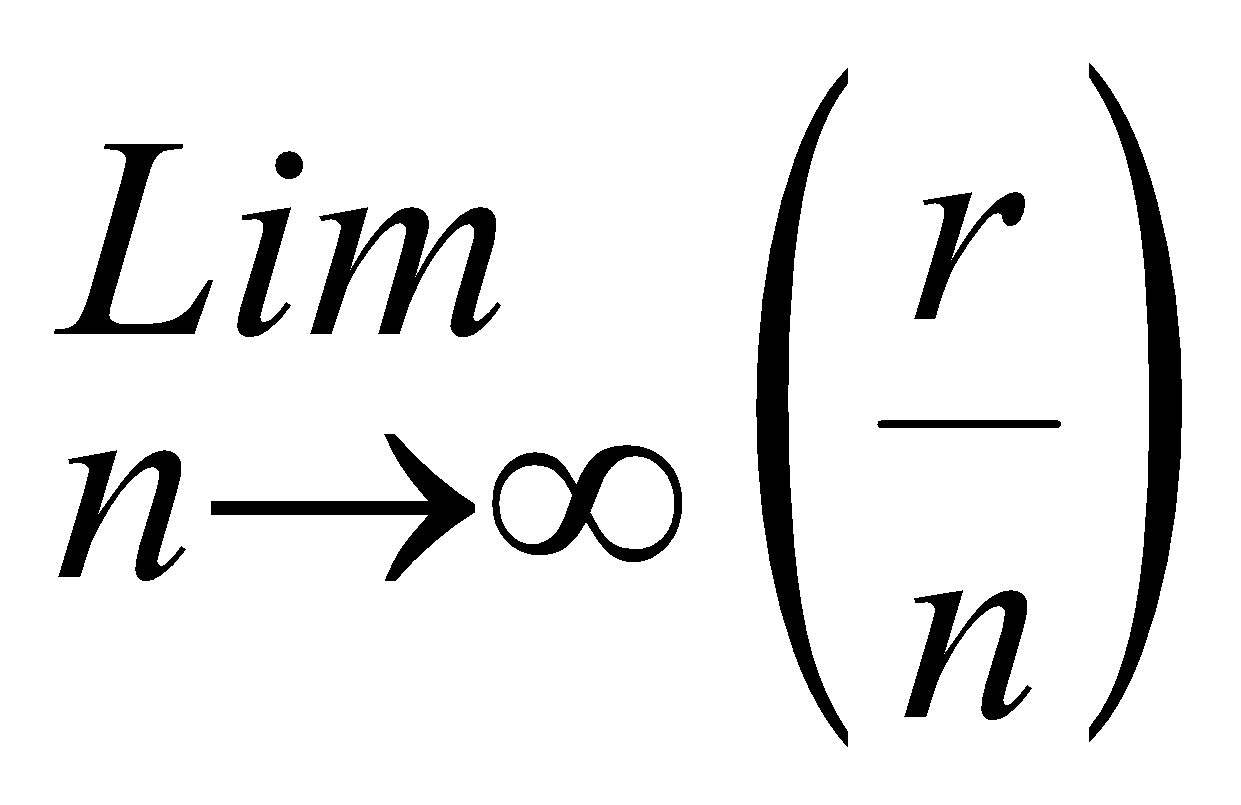for the least and the greatest values of r respectively. In general
AREAS OF BOUNDED REGIONS
- Area bounded by curve y = f(x) the ordinates x = a, x = b and x–axis. is given by
- Area bounded by curve x = f(y), the abscissae y = c, y = d and y-axis is given by
- Area bounded by the curves y = f(x) and y = g(x) is given by
where, a and b are the ordinates of points of intersection
SOME VERY IMPORTANT DEFINITE INTEGRALS
[When m and n both even]
[when either of m & n is odd]
These are called WALLI’S FORMULA
, n is even
, n is odd
Study Notes for JEE Main/JEE Advanced/BITSAT
