DIFFERENTIAL EQUATIONS
INTRODUCTION
An equation that involves an independent variable, dependent variable and differential coefficients of dependent variable with respect to the independent variable is called a DIFFERENTIAL EQUATION. For example,
ORDER AND DEGREE OF A DIFFERENTIAL EQUATION
ORDER of a differential Equation is the order of the highest derivative occuring in the equation.
DEGREE of a differential equation is the degree (exponent) of the derivative of the highest order in the equation after the equation is freed from negative and fractional powers of the derivatives.
For example, consider the differential equations written above.
Example (i) The equation is of the FIRST ORDER and FIRST DEGREE.
Example (ii) The equation is of the FIRST ORDER and FIRST DEGREE.
Example (iii) The equation is of the FIRST ORDER and FIRST DEGREE.
Example (iv) The equation is of the SECOND ORDER and FIRST DEGREE.
Example (v) The equation is of the SECOND ORDER and SECOND DEGREE.
[Note that the degree of  is 3 but it is not the degree of the equation.]
is 3 but it is not the degree of the equation.]
Example (vi) It is the FIRST ORDER, FIRST DEGREE equation.
Example (vii) It is the FIRST ORDER, FIRST DEGREE equation.
Example (viii) It is the FIRST ORDER, FIRST DEGREE equation.
Example (ix) Rewrite the equation as follows :
The equation is of the FIRST ORDER and SECOND DEGREE
Example (x) Rewrite the equation as follows :
The equation has SECOND ORDER and SECOND DEGREE.
Example (xi) Rewrite the equation as follows :
The equation has FIRST ORDER and SECOND DEGREE
Example (xii) The equation is of the SECOND ORDER. The degree of the equation is not defined as the equation is not expressible as the integral powers of the derivatives.
Example (xiii) Rewrite the equations as follows :
The equation is FIRST ORDER and FIRST DEGREE.
Note that if the equation be
Then it is FIRST ORDER and nth DEGREE equation
LINEAR AND NONLINEAR DIFFERENTIAL EQUATIONS
A differential equation is said to be LINEAR if the dependent variable and all of its derivatives occuring in the equation, occur only in the first power and there are no product of these. A linear equation of nth order can be written in the form
Where, P0, P1, P2,......, Pn–1 and Q must be either constants or functions of ‘x’ only.
A linear differential equation is always of the first degree but every differential equation of the first degree need not be linear.
For example, the equations ;
;  ;
; are not linear.
are not linear.
SOLUTION OR INTEGRAL OF DIFFERENTIAL EQUATION
A solution or an integral of a differential equation is a relation between the variables, not involving the differential coefficients, such that this relation and the derivatives obtained from it satisfy the given differential equation. For example,
GENERAL SOLUTION
If the solution of the differential equation contains as many independent arbitrary constants as the order of the differential equation then it is called the general solution or the complete integral of the differential equation.
For example, in the previous example , is the general solution of the equation
, is the general solution of the equation because it contains two arbitrary constants A and B, which is equal to the order of the equation.
because it contains two arbitrary constants A and B, which is equal to the order of the equation.
PARTICULAR SOLUTION
Solution obtained by giving particular values to the arbitrary constants in the general solution is called a particular solution. For example, in the previous example if A = B = 1, then y = cos x + sin x is a particular solution of the differential equation  .
.
Solution of a differential equation is also called its PRIMITIVE.
FORMATION OF DIFFERENTIAL EQUATION
In an equation involving n arbitrary constants, a differential equation of nth order can be obtained by eliminating these n arbitrary constants.
PROCEDURE
- Suppose we have a given equation with n arbitrary constants f (x, y, c1,c2,.....,cn) = 0
- Differentiate the equation successively n times to get n equations.
- Eliminating the arbitrary constants from these n + 1 equations leads to the required differential equation.
Example :
Form a differential equation of the family of curves represented by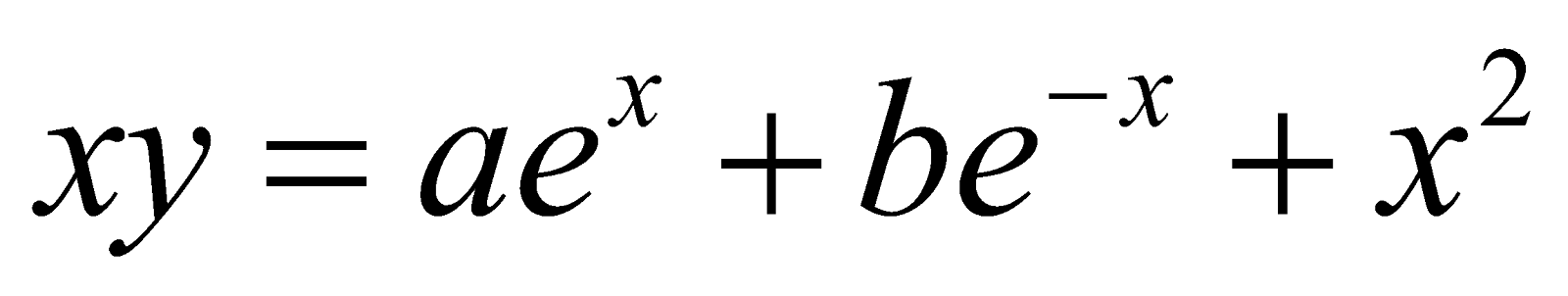 , where a and b are arbitrary constants.
, where a and b are arbitrary constants.
Solution :
The given equation is 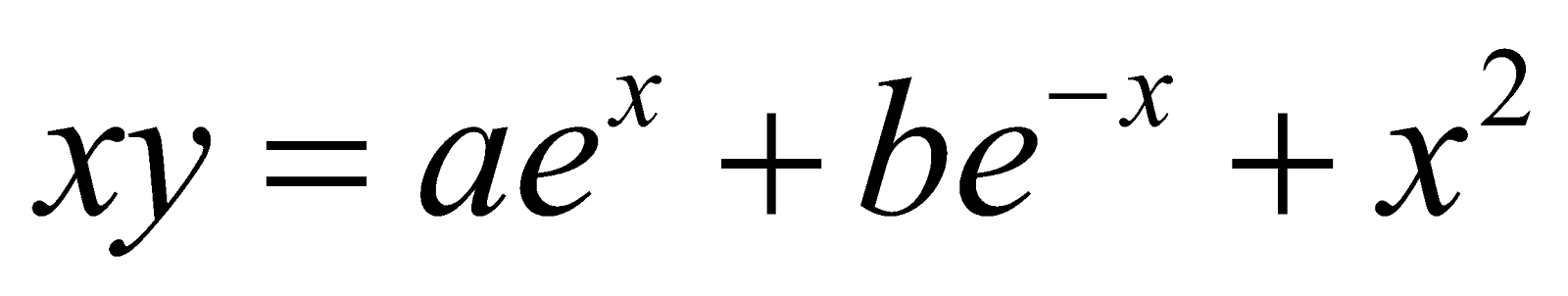 ...(i)
...(i)
This equation has two arbitrary constants, therefore we will get a second order differential equation. Differentiating the equation (i) twice with respect to x, we get
We have to eliminate a and b from these three equations.
From (i)  , put in (iii)
, put in (iii)
we get  which is the required differential equation.
which is the required differential equation.
SOLUTIONS OF DIFFERENTIAL EQUATIONS OF THE FIRST ORDER AND FIRST DEGREE
A differential equation of first order and first degree can be expressed in any one of the following forms:
All the differential equations are not integrable. A very limited standard forms of differential equations can only be solved, some of which are discussed below :
VARIABLES SEPARABLE FORM
If the equation can be reduced to the form f (x) dx + g (y)
dy = 0, we say that the variables have been separated. On integrating this reduced form we get where c is any arbitrary constant.
where c is any arbitrary constant.
dy = 0, we say that the variables have been separated. On integrating this reduced form we get
DIFFERENTIAL EQUATION REDUCIBLE TO VARIABLES SEPARABLE FORM
A differential equation of the form  ...(i)
...(i)
can be reduced to variables separable form by substituting
The equation (i) then becomes
Hence the variables are separated in terms of z and x.
HOMOGENEOUS DIFFERENTIAL EQUATIONS
A function f(x, y) is said to be homogeneous of degree n if 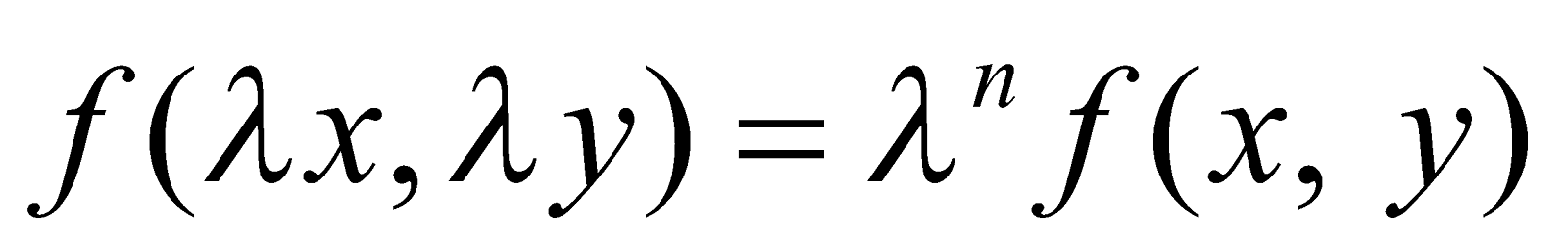
Alternatively, a homogeneous function f (x, y) of degree n can be expressed as 
Suppose a differential equation can be expressed in the form 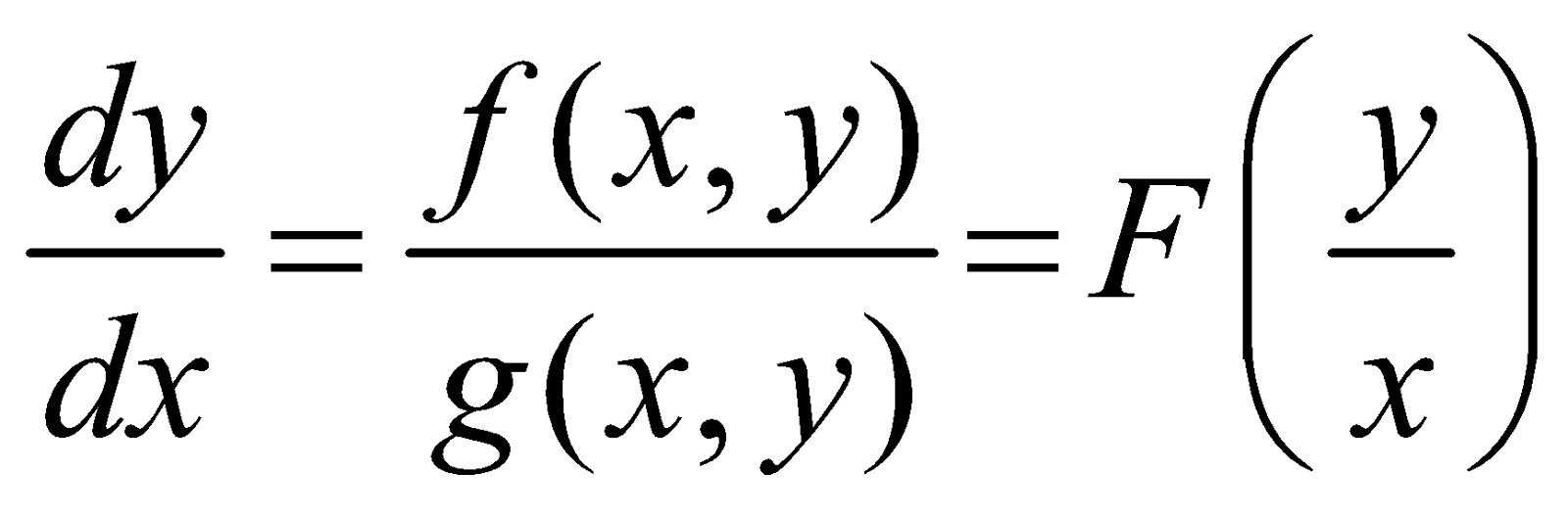
Where f (x, y) and g (x, y) are homogeneous functions of same degree. To solve such types of equations we put 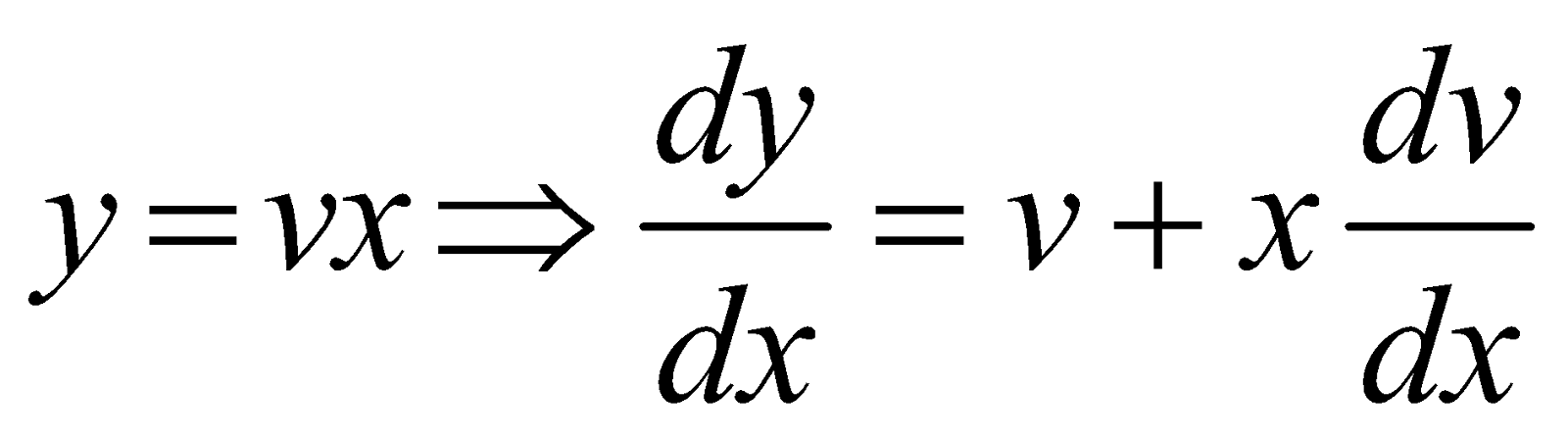 . The given equation then reduces to
. The given equation then reduces to 
Hence, the variables are separated in terms of v and x.
DIFFERENTIAL EQUATIONS REDUCIBLE TO HOMOGENEOUS EQUATIONS
The differential equation of the form
can be reduced to a homogeneous form by changing the variables
x = X + h, y = Y + k, where, h and k are constants to be chosen so as to make the given equation homogeneous. we have
The equation (i) becomes
We choose h and k so as to satisfy a1h + blk + c1 = 0 and a2h + b2k + c2 = 0
On solving we get,
For these values of h and k, the equation (ii) reduced to  , which is a homogeneous form and will be solved by putting Y = VX.
, which is a homogeneous form and will be solved by putting Y = VX.
[In case  (say), then the original equation is
(say), then the original equation is , which is an equation that can be reduced to variables separable form by substituting
, which is an equation that can be reduced to variables separable form by substituting  (see Differential equation discussed under head 2)]
(see Differential equation discussed under head 2)]
LINEAR DIFFERENTIAL EQUATIONS
A linear differential equation of the first order can be either of the following forms
(i)  , where P and Q are functions of x or constants.
, where P and Q are functions of x or constants.
(ii)  , where R and S are functions of y or constants.
, where R and S are functions of y or constants.
Consider the differential equation (i) i.e 
Multiply both the sides by 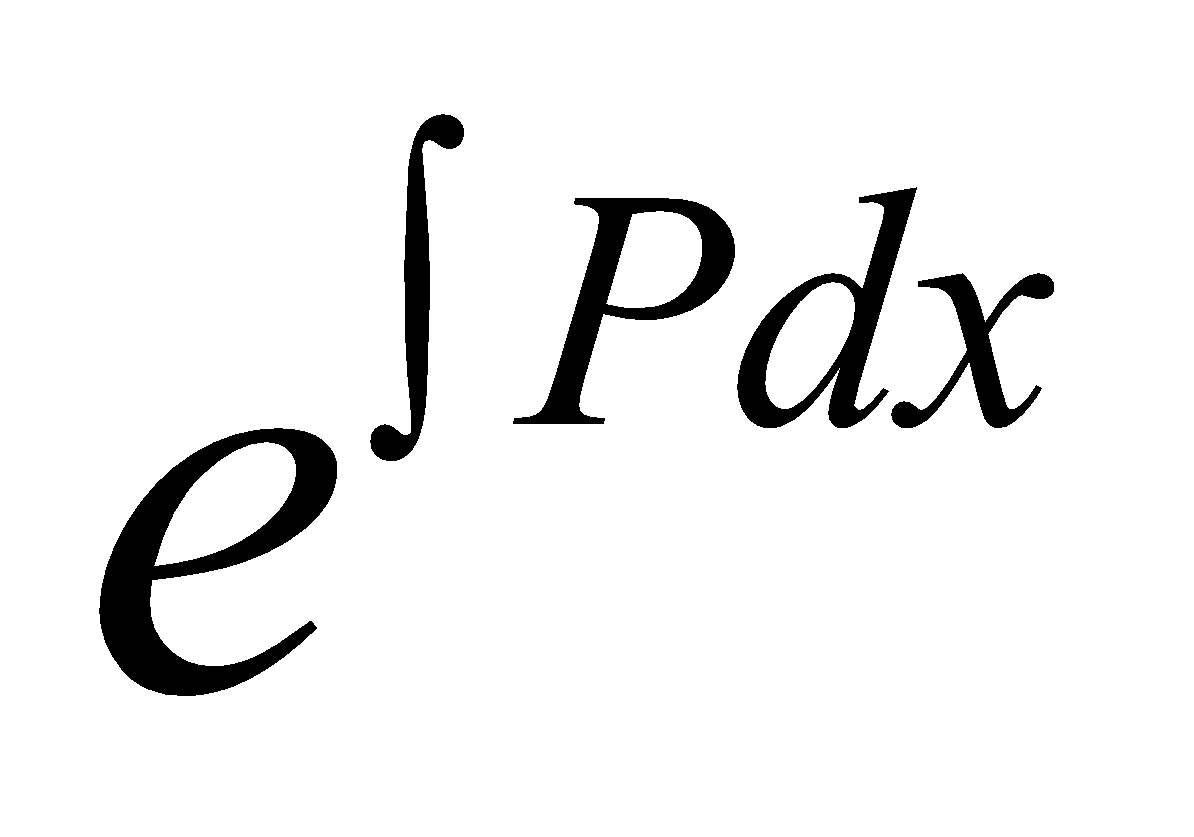 to get
to get 
Integrating, we get 
which is the general solution of the given equation. The expression  is called the INTEGRATING FACTOR of the equation.
is called the INTEGRATING FACTOR of the equation.
Therefore, The solution can also be written as 
where, I.F. = Integrating Factor = 
[For the second differential equation , the integrating factor, I.F. = and the general solution is
, the integrating factor, I.F. = and the general solution is
x (I.F.) =  ]
]
DIFFERENTIAL EQUATION REDUCIBLE TO LINEAR FORM
- Bernoulli’s Equation : An equation of the form , where P and Q are functions of x alone or constants, is called
Bernoulli’s equation.
Divide both the sides by yn, we get 
Put 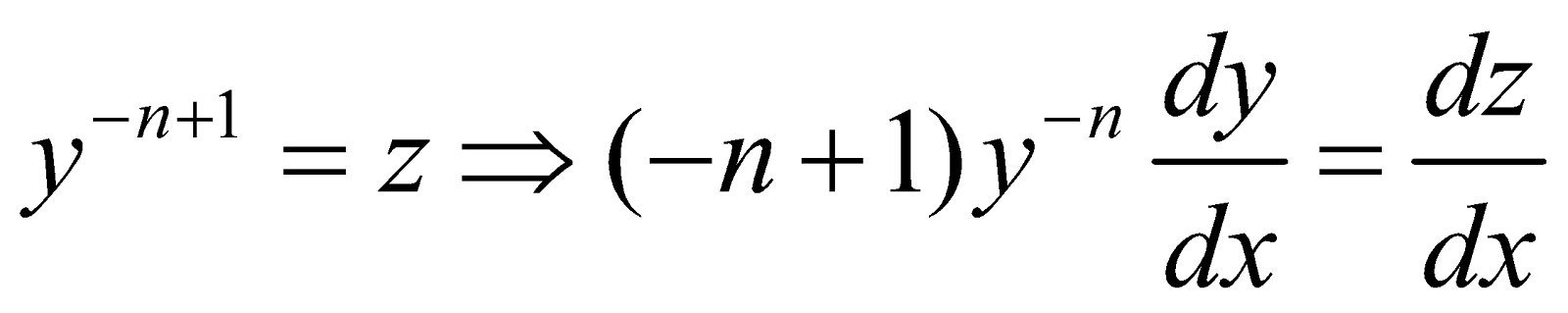 .
.
The equation reduces to 
Which is linear in z and can be solved in the usual manner.
- Equation of the form
, where P and Q are functions of x alone or constants
Divide both the sides by h (y), we get
Let  then
then
Hence the equation becomes 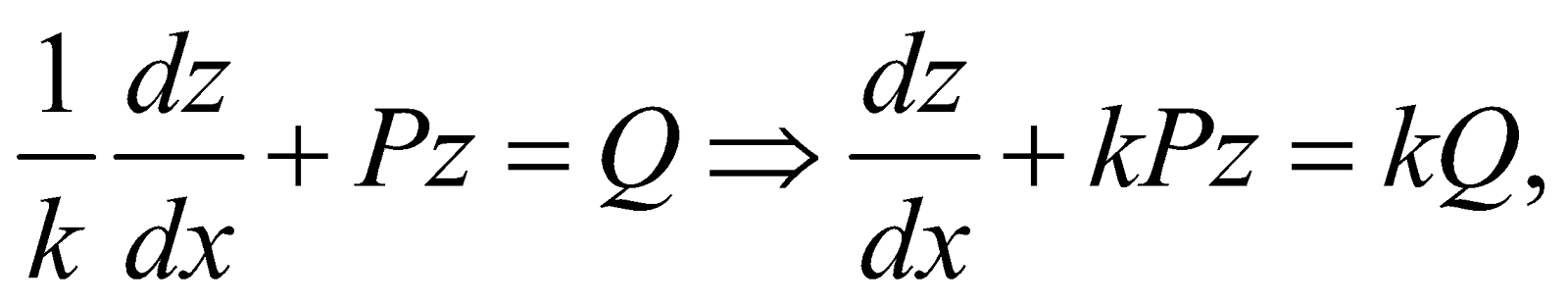 which is linear in z.
which is linear in z.
SOLUTION OF DIFFERENTIAL EQUATION BY INSPECTION
APPLICATION OF DIFFERENTIAL EQUATIONS IN CARTESIAN GEOMETRY
Let y = f (x) represents a curve in the cartesian plane.
We know that the derivative  represents the slope of tangents to the curve at a point P(x, y) of the curve.
represents the slope of tangents to the curve at a point P(x, y) of the curve.
From the figure PN = y and , where PT is the tangent to the curve at P. We define
, where PT is the tangent to the curve at P. We define
OP = radius vector of 
PT = tangent at P = PN cosec ψ
PG = normal at P = PN sec ψ
TN = cartesian subtangent
GN = cartesian subnormal
Further, the equation of tangent at P is
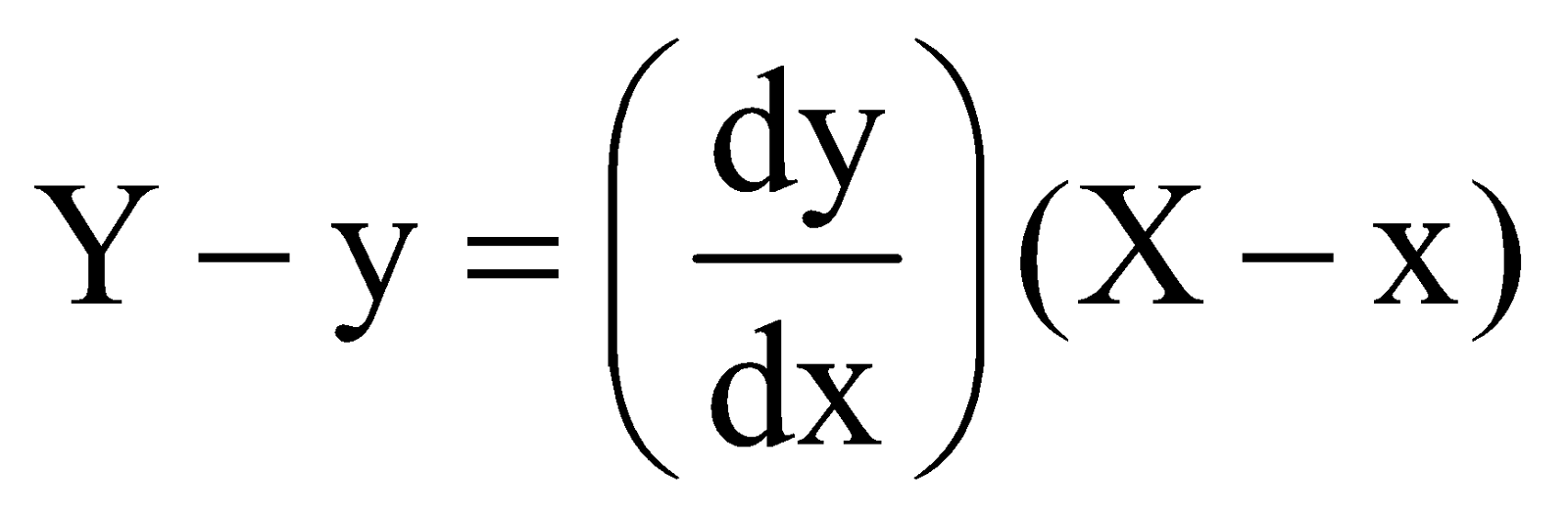
and the equation of normal at P is








