FUNCTIONS

INTRODUCTION

The function has already been defined in the chapter of “Sets, Relations and Functions” as a special kind of relation. However, we rarely use a function in that form. We will define a function in slightly different way as following.

Let A and B be two sets. Let ‘f’ is a rule which associates to each member of A a member of B then ‘f’ is said to be a function from A into B. Symbolically, we write.

The set A is said to be DOMAIN and the set B is said to be CO-DOMAIN of the function f.
If x denotes a member of the set A and y is a member of the set B, which the function f associates to x, then we write y = f(x)

y is called the IMAGE of x under the function f
x is called the PER-IMAGE of y.

The set of all the images (or function values) is called RANGE of f. Thus

Range of f = {f (x) : x∈A} ⊆ B. Range of f is also denoted by f (A).

If y = f(x) is a function of x such that for every value of x in its domain, there corresponds a unique value of y, then y = f(x) is said to be a SINGLE VALUED FUNCTION of x. In general the function wherever used onwards always means single valued function which is identical to the function defined in relations.
Hence, If is a function (a single valued function), then

Each element of A must have exactly one image in B, i.e., no element of A should be without an image and no element of A can have more than one image.
Two or more element in A may have same image in B.
There may be some elements in B which are not images of elements of A.

INDEPENDENT AND DEPENDENT VARIABLES

The symbol which denotes a member of the domain of function (usually denoted by x) is called an independent variable and the symbol denoting member of the range of function (usually denoted by y) is called a dependent variable.

REAL VALUED FUNCTION (OR REAL FUNCTION)

The function for which the domain and range are the subsets of the set of real number R is called a real function.

WAYS OF DEFINING A REAL FUNCTION

UNIFORM DEFINITION

If a function is defined as y = f(x),
x∈[a, b], we say that it is uniformly defined.

For example :

y = f(x) = sin x, x ∈ R
y = f(x) = x2 + 1, x ∈ [–1, 1]

PIECEWISE DEFINITION

If a function y = f(x), x∈[a, b] assumes different forms in different subsets of [a, b], we say that it is piecewise defined.

For example :

EXPLICIT AND IMPLICIT FUNCTIONS

EXPLICIT FUNCTIONS

A function is said to be an explicit function if it is expressed in the form y = f(x). That is the dependent variable y is expressible completely in terms of the independent variable x.

For example :

IMPLICIT FUNCTIONS

A function is said to be an implicit function if it is expressed in the form f(x, y) = C, where C is a constant. That is y is not directly expressible in terms of x.

For example :

Note : A function given in the implicit form may be reduced (though not always) to an explicit form. Further, most of the implicit functions are not single valued.

For example :

is implicit function

is its explicit form.

CLASSIFICATION OF REAL FUNCTIONS

Real functions are generally classified under two heads ALGEBRAIC FUNCTIONS and TRANSCENDENTAL FUNCTIONS.

ALGEBRAIC FUNCTIONS

Algebraic functions are normally of three kinds :

Polynomial Function : If a function y = f(x) is given by

where, a0, a1, a2, .......an are real numbers and n is any non negative integer, then f(x) is called a polynomial function in x.

If a0≠ 0, then the degree of the polynomial f(x) is n. The domain of a polynomial function is the set of real numbers R.

For example :

is a polynomial of degree 5.

Rational Functions : If a function y = f(x) is given by

where φ (x) and ψ(x) are polynomial functions, then f(x) is called a rational function in x.

Domain of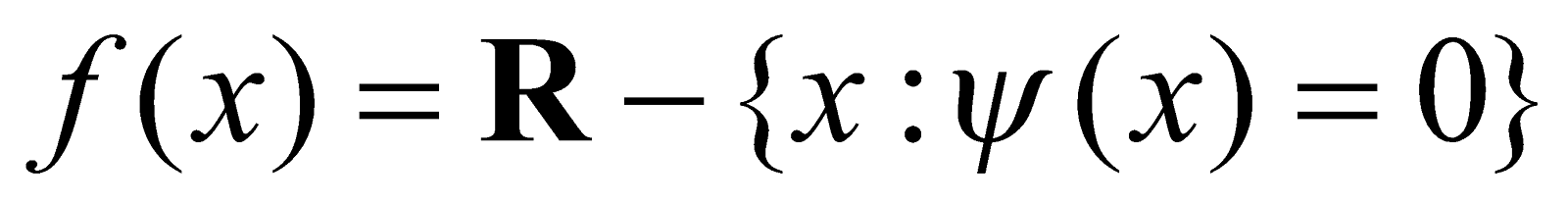

For example :

Irrational Functions : The algebraic functions containing one or more terms having non-integral rational powers of x are called irrational functions.

For example :

TRANSCENDENTAL FUNCTION

A function, which is not algebraic, is called a transcendental function. Trigonometrical, Inverse trigonometric, Exponential, Logarithmic, etc. are transcendental functions.

GRAPH OF FUNCTION

Let f be a function with domain [a, b] and y = f(x), x∈[a, b]. The set of points (x, y) obtained by giving different values of x on a rectangular coordinate system is said to be the graph of the function f and y = f(x) is said to be the equation of the graph. The horizontal extent of graph gives the domain of the function and the vertical extent of graph represents the range of the function.

GRAPH OF SOME REAL FUNCTIONS

CONSTANT FUNCTION

Let c be a fixed real number. The function that associates to each real number x, this fixed number c, is called a constant function.

That is y = f(x) = c for all x∈R

The domain of f (x) = R. The range of f (x) = {c}

There are as many constant functions as there are real numbers. The graph of the constant function is shown in the above figure, which is a straight line parallel to x -axis at a distance c from origin.

IDENTITY FUNCTION

The function that associates to each real number x the same number x, is called the identity function. That is

The domain of f(x) = R. The range of f(x) = R

The graph of the identity function is shown in the figure, which is a straight line passing through origin inclined at an angle 45° to x-axis.

LINEAR FUNCTION

If a and b be fixed real numbers, then the linear function is defined as

y = f(x) = ax + b, a and b are constants.

The domain of f(x) =R. The range of f(x) = R

The graph of a linear function is given in the following diagram, which is a straight line with slope a

QUADRATIC FUNCTIONS

If a, b, c, are fixed real numbers, then the quadratic function is expressed as

which is equation of a parabola, downward if a < 0 and upward if a > 0 and vertex at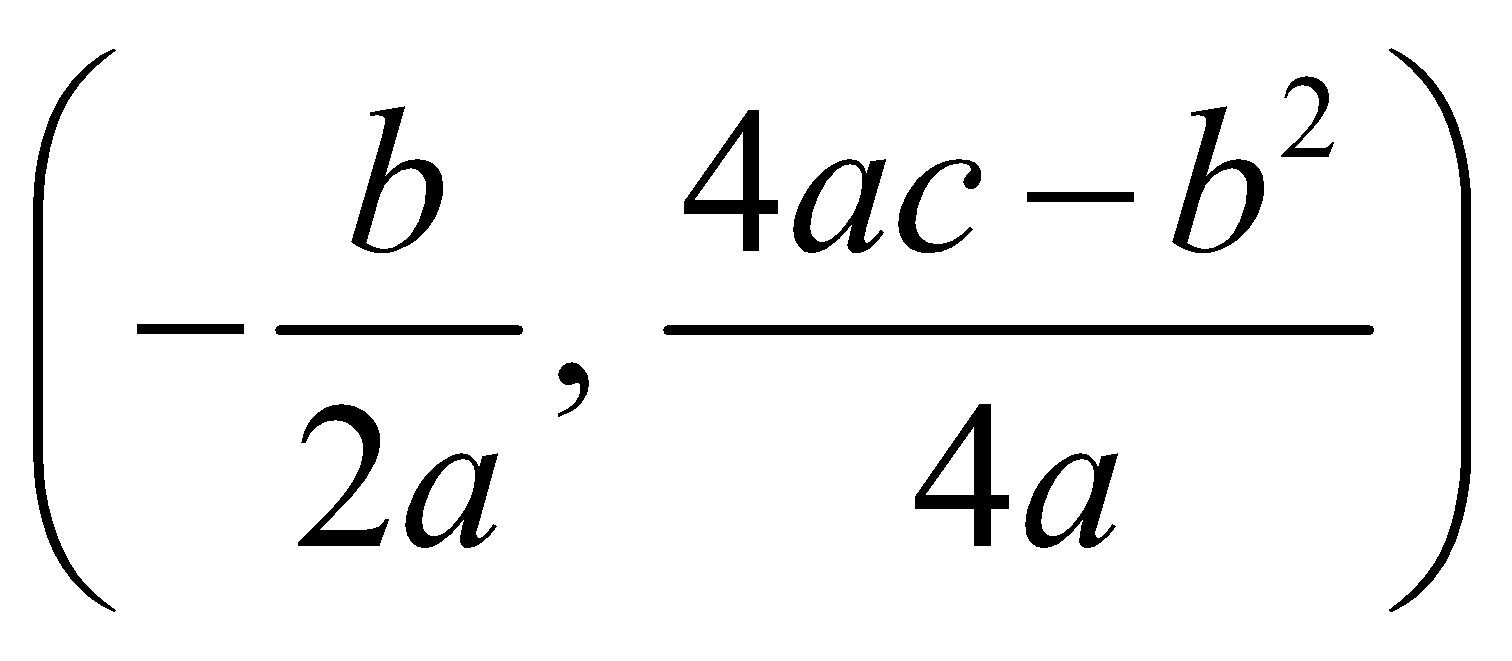

[see Parabolas in the Chapter of Conic Sections]

The domain of f(x) = R

The range of f(x) is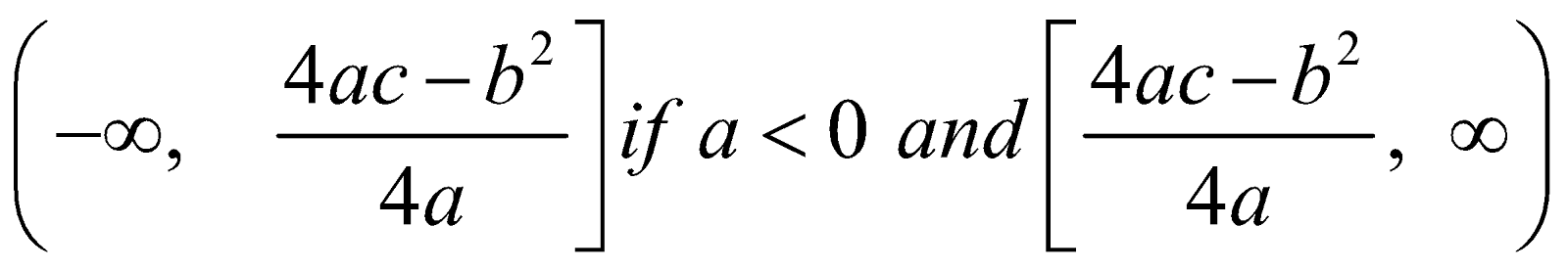

if a > 0

SQUARE ROOT FUNCTION

Square root function is defined by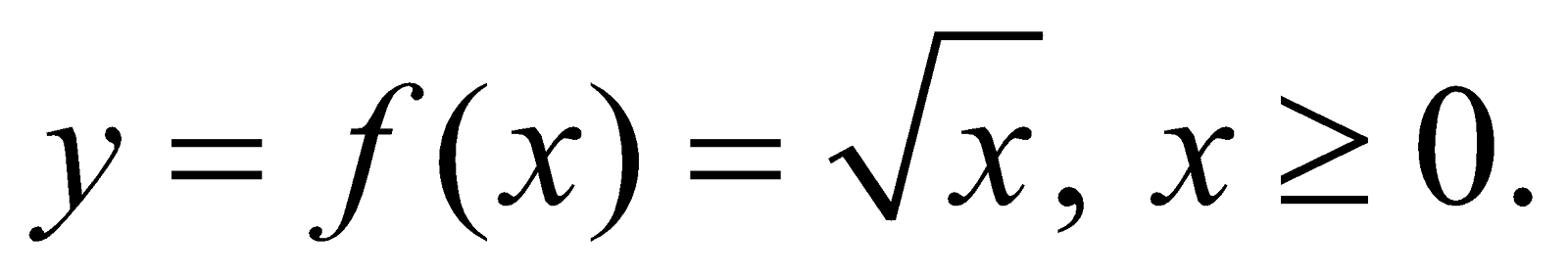

Domain of f(x) = [0, +∞). Range of f(x) = [0, +∞)

The graph of square root function is shown in the adjacent figure, which is a semi-parabola.

MODULUS FUNCTION (OR ABSOLUTE VALUE FUNCTION)

Modulus function is given by

y = f(x) = |x|, where |x| denotes the absolute value of x, that is

Domain of f(x) = R. Range of f(x) = [0, + ∞)

The graph of modulus function is as shown in the figure. It consists of two straight lines

y = x and y = –x above the x-axis.

SIGNUM FUNCTION

Signum function is defined as follows

Symbolically, signum function is denoted by sgm (x)

Thus, y = f(x) = sgm (x)

where sgm (x)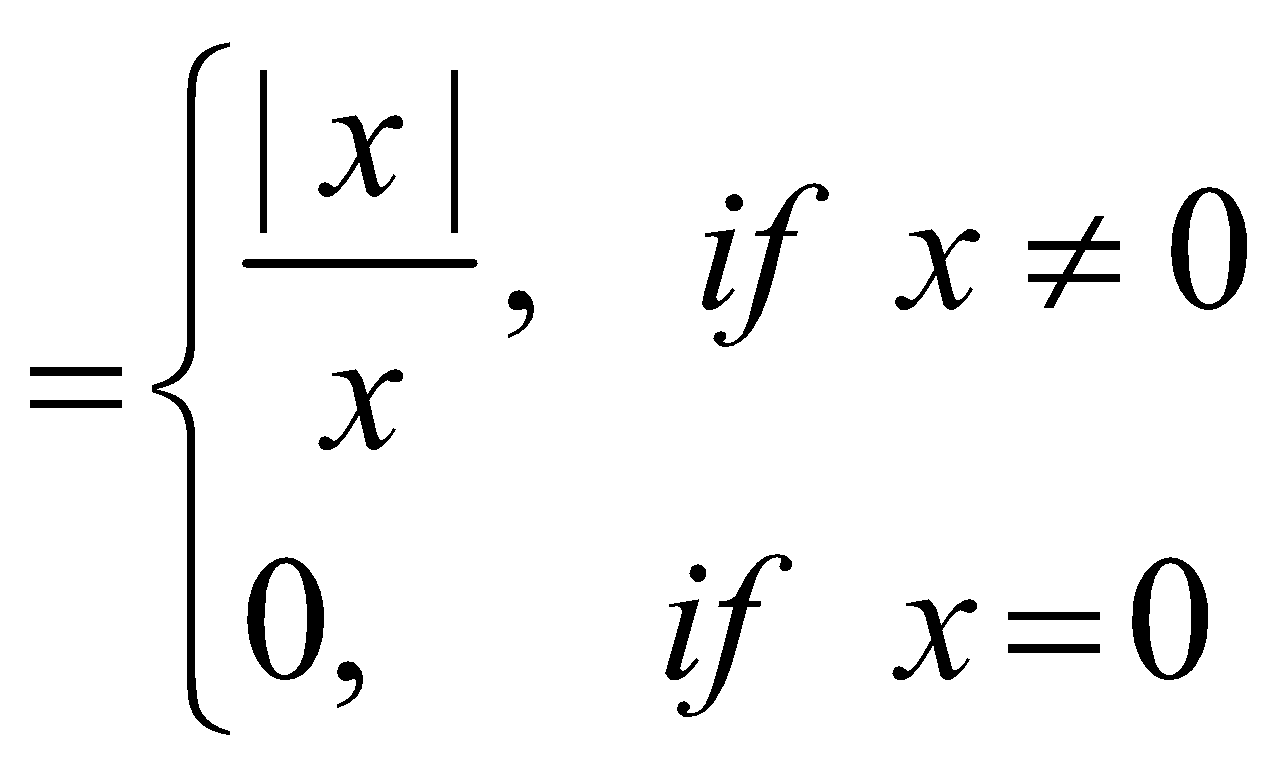

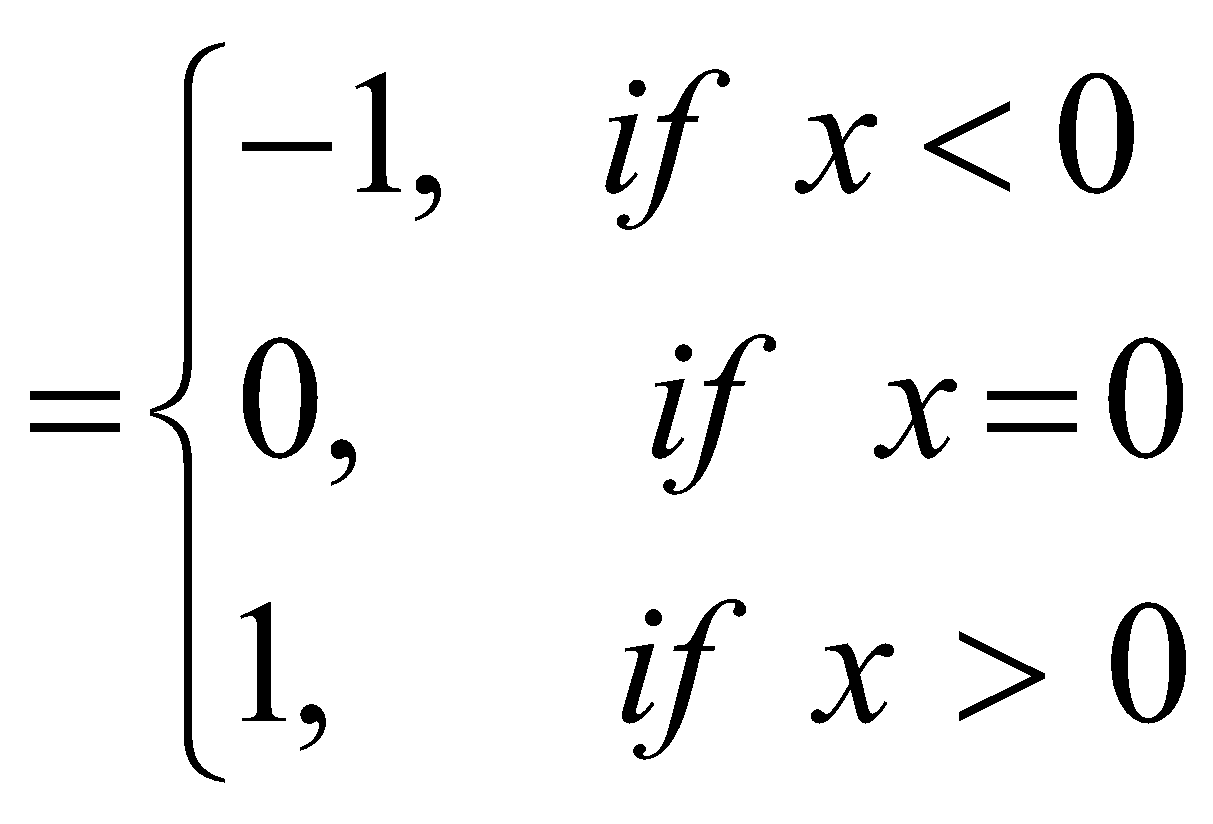
Domain of sgm (x) = R

Range of sgm (x) = {–1, 0, 1}

The graph of signum function is shown in the figure, which consists of two parallel lines.

y = –1 and y = 1 and an isolated point O (0, 0)

[Note that the circles () at one end of the lines represent that these points (viz, (0, 1) and (0, –1) are not included in the graph. The dot (•) indicates that the point (0, 0) is included in the graph.]

THE GREATEST INTEGER FUNCTION

The greatest integer function is defined as y = f (x) = [x], where [x] represents the greatest integer less than or equal to x. That is for any integer n, [x] = n if n ≤ x < n + 1

For example :

;

an integer;

etc.

To draw its graph we may divide the domain into intervals as below :

If 0 ≤ x < 1, [x] = 0

If 1≤ x < 2, [x] = 1

If 2 ≤ x < 3, [x] = 2

.....................

......................

If –1 ≤ x < 0, [x] = –1

If –2 ≤ x < –1, [x] = –2

The graph of the function is as shown in the figure, which consists of pieces of straight lines parallel to x-axis representing y = n, .

Domain of f(x) = R; Range of f(x) = I

EXPONENTIAL FUNCTIONS

Exponential Function is given by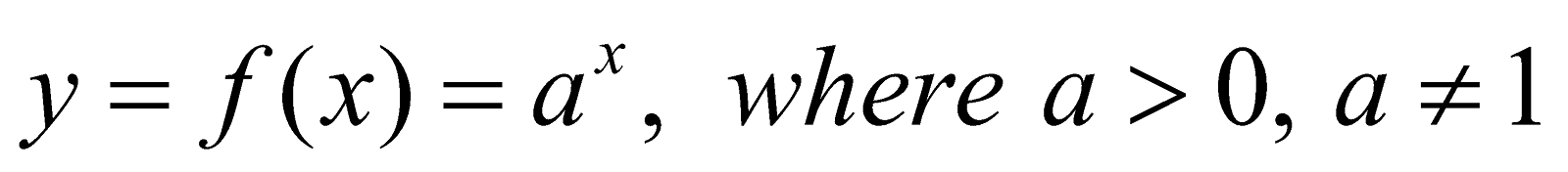

The graph of the function is as shown below, which is increasing if a>1 and decreasing if 0<a<1

Domain of f(x) = R

Range of f(x) = (0, +∞)

PROPERTIES OF EXPONENTIAL FUNCTIONS

y = f(x) = ex is a particular form of above, when a = e

LOGARITHMIC FUNCTIONS

A logarithmic function may be given by y = f(x) = logax, where a > 0, a ≠1 and x > 0

The graph of the function is as shown below, which is increasing if a>1 and decreasing if 0<a <1.

Domain of f(x) = {x ∈R : x > 0} = (0, + ∞)

Range of f(x) = R

PROPERTIES OF LOGARITHMIC FUNCTIONS

y = f(x) = logex (or ln x) is a particular form of above, when a = e.

POWER FUNCTION

The power function is given by y = f (x) = xn, n ∈I, n ≠ 1, 0

The graph of y = f (x), its domain and range depend on n.

If n is positive even integer

(e.g. f(x) = x2, x4,.....)

Domain of f(x) = R

Range of f (x) = [0, + ∞)

If n is positive odd integer

(e.g. f(x) = x3, x5,......)

Domain of f(x) = R; Range of f (x) = R

If n is negative even integer (e.g. f(x) = x–2, x–4, ....)

Domain of f(x) = R – {0}

Range of f(x) = (0, +∞)

If n is negative odd integer

(e.g. f(x) = x–1, x–3,.......)

Domain of f(x) = R - {0}; Range of f(x) = R - {0}

TRIGONOMETRIC FUNCTIONS AND INVERSE TRIGONOMETRIC FUNCTIONS

The graph of different trigonometric functions, their domains and range have been discussed in Trigonometry

OPERATIONS ON REAL FUNCTIONS

Let

be two real functions then,

SUM
The sum of the functions f and g is defined assuch that (f + g) (x) = f (x) + g (x)
PRODUCT
The product of the functions f and g is defined assuch that (fg)(x) = f(x) g (x)

Clearly f+g and fg are defined only if f and g have the same domain. In case, the domain of f and g are different. Then, Domain of f + g or fg = Domain of f ∩ Domain of g.

MULTIPLICATION BY A NUMBER

Let

be a function and let k be a real number. Then we define

such that (kf) (x) = kf (x) x ∈ X

COMPOSITION (FUNCTION OF FUNCTION)

Let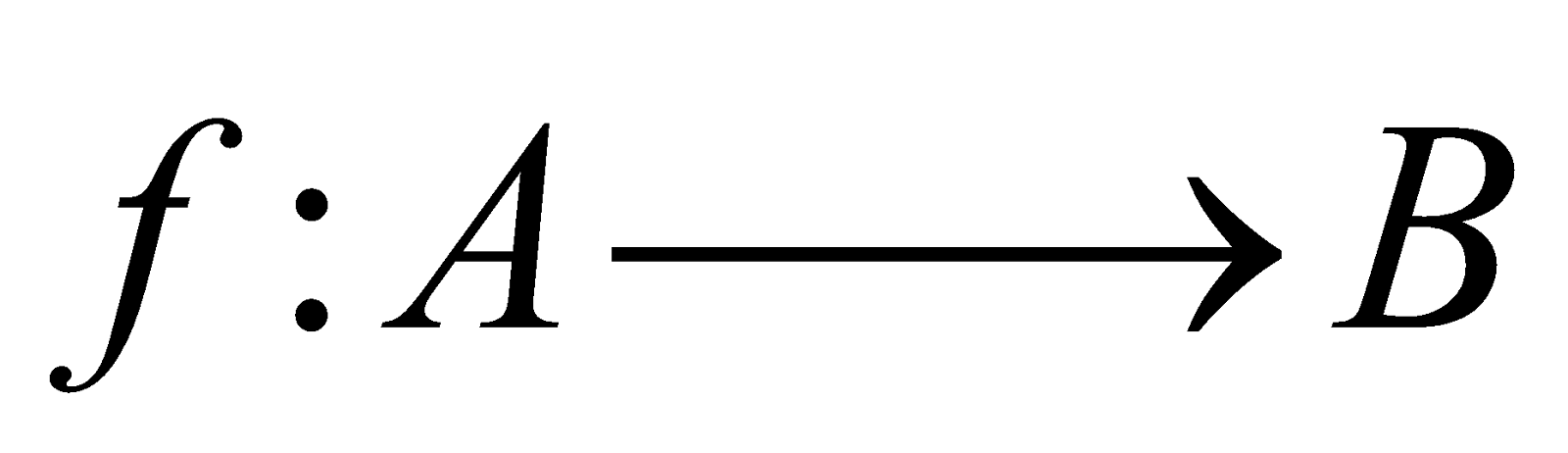

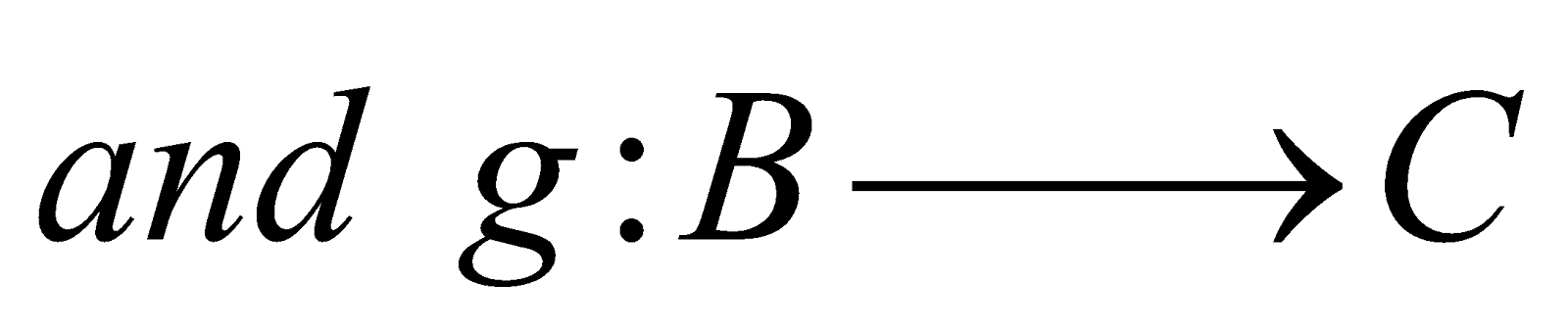be two functions.

We define

such that

Alternate, there exists y∈B such that

If f(x) = y and g(y) = z then gof (x) = z

For example :

Then

and

Alternate :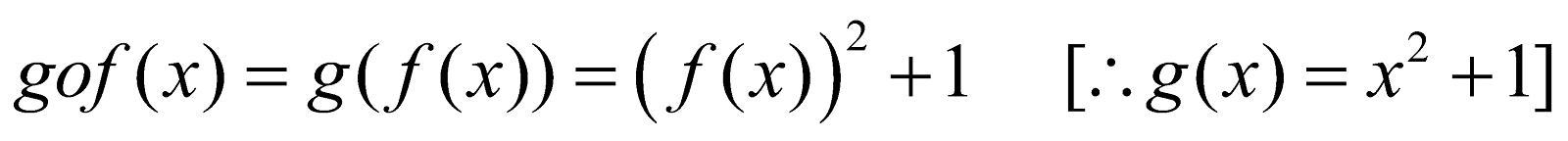

and

If f (x) = x2 and g (x) = sin x

Then fog (x) = sin2x and gof (x) = sin x2

THEOREMS

gof ≠ fog
(fog) oh = fo (goh)

DIFFERENT TYPES OF FUNCTIONS (MAPPINGS)

ONE-ONE AND MANY-ONE-FUNCTION

The mapping

is called one-one function if different elements in A have different images in B. Such a mapping is also known as Injective function or an injection or Monomorphism.

METHODS TO TEST ONE-ONE

Analytically : If thenor Equivalently
Graphically : If any line parallel to x-axis cuts the graph of the function at most at one point, then the function is one-one.
Monotonically : Any function, which is entirely increasing or decreasing in whole domain, then f(x) is one-one. That is the derivative of f(x) is either entirely positive or entirely negative.

NUMBER OF ONE-ONE FUNCTIONS

Let

be a function such that A and B are finite sets having m and n elements respectively, (where n > m)

Then number of one-one functions = n (n – 1) (n – 2) .....(n – m + 1)

The function

is called many -one function if two or more than two different elements in A have the same image in B.

ONTO (SURJECTIVE) AND INTO FUNCTIONS

If the function

is such that each element in B (co-domain) is the image of at least one element in A, then we say that f is a function of A ‘onto’ B. Thus,

such that f(A) = B i.e., Range = Co-domain

Note : Every polynomial function

of degree odd is ONTO.

NUMBER OF ONTO (SURJECTIVE) FUNCTIONS FROM A TO B

Let

be a map such that A and B are finite sets having m and n elements respectively such that 1 ≤ n ≤ m, then number of onto (surjective) functions from A to B is

= coefficient of xn in n! (ex – 1)r

is such that there exists at least one element in co-domain which is not the image of any element in domain, then f(x) is into.

Thus,

such that

i.e.,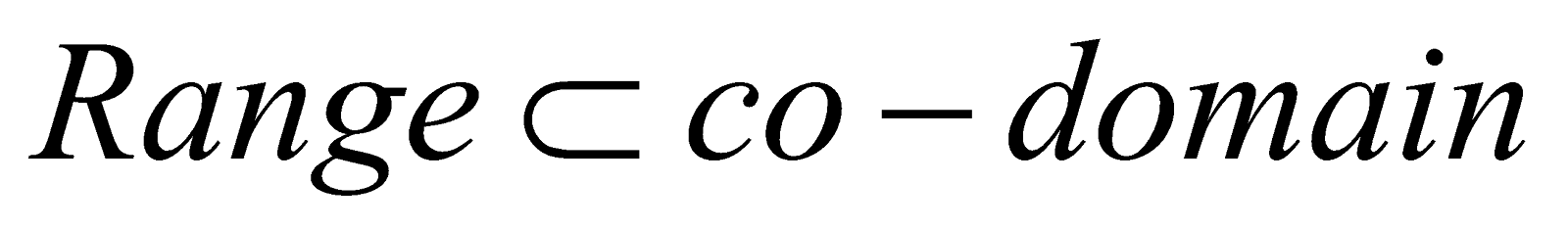

THEOREMS

If f and g are injective, then fog is injective
If f and g are surjective, then fog is surjective
If f and g are bijective, then fog is bijective
One-one functions, Onto Functions, Many-one function, Into functions and Bijective functions have already been discussed in the Chapter Sets, Relations and Mapping.

INVERSE OF A FUNCTION

Let f : A

B is a bijective function, i.e. it is one-one and onto both.

We define g : B

A such that f(x) = y

g(y) = x

g is called inverse of f and vice versa. Symbolically we write g = f–1

Thus f(x) = y

f–1(y) = x

THEOREMS

If the inverse of f exists, it is called an INVERTIBLE FUNCTIONS.
f–1 is also a bijective function
f : A B is invertible iff there exists

g : B

A such that gof = IA and fog = IB

where IA is identity function on A and IB is identity function on B

If f and g are bijective functions then

EVEN AND ODD FUNCTIONS

EVEN FUNCTIONS

A real function f(x) is an even function if f (–x) = f(x) or f(x) – f(–x) = 0

For example :

f (x) = x2 is even as f(–x) = (–x)2 = x2 = f (x)
f (x) = cos x is even as f(–x) = cos (–x) = cos x = f(x)

ODD FUNCTIONS

A real function f(x) is said to be an odd function if f (–x) = – f (x) or f(x) + f(–x) = 0

For example :

f (x) = tan x is odd as f (–x) = tan (–x) = – tan x = – f(x)
f (x) = x3 – 4x is odd as f(–x) = (–x)3 – 4 (–x) = –x3 + 4x = – f(x)

IMPORTANT RESULTS

Even function ± Even function = Even function, for example f(x) = x2+ cos x, is even.
Odd function ± Odd function = Odd function, for example f (x) = x3 – sin x + tan x, is odd.
Even function ± Odd function = neither even nor odd, for example f(x) = sin x + cos x, is neither even nor odd.
Even function × Even function = Even function, for example f(x) = x2 cos 2x, is even.
Odd function × Odd function = Even function, for example f(x) = x sin x, is even.
Odd function × Even function = Odd function, for example f(x)= x5 tan2x, is odd.
gof or fog is even if any one of f and g or both even.

For example : f(x) = cos x2 is even

f(x) = sec x5 is even
f(x) = (sin x)4 is even

gof or fog is odd if both of f and g are odd, for example f(x) = tan x5 is odd.
If f (x) is an even function then is odd and if f(x) is an odd function then is even.
The graph of an even function is symmetrical about y-axis.
The graph of an odd function is symmetric about origin or symmetrical in opposite quadrants
An even function can never be one-one, however an odd function may or may not be one-one.
A constant function is even function
The function is both even and odd.
For any function f(x), f(x) + f(–x) is an even function, where as f(x) – f(–x) is an odd function.

Thus, every function f(x) can be expressed as the sum of an even function and an odd function

For example :

Let f(x) = x3 – x2 + 1

f(–x) = –x3 – x2 + 1

Obviously f(x) is neither even nor odd.

Now, f(x) +f(–x) = – 2x2 +2, which is even and f(x) – f(–x) = 2x3, which is odd

PERIODIC FUNCTIONS

A function f(x) is said to be a periodic function of x, provided there exists a real number T > 0 such that

The smallest positive real number T, satisfying the above condition is known as the period or the fundamental period of f(x).

TESTING THE PERIODICITY OF A FUNCTION

Putand solve this equation to find the positive values of T independent of x.
If no positive value of T independent of x is obtained, then f(x) is a non-periodic function.
If positive values of T independent of x are obtained, then f(x) is a periodic function and the least positive value of T is the period of the function f(x).

IMPORTANT RESULTS

Constant function is periodic with no fundamental period.
If f(x) is periodic with period T, then and are also periodic with same period T.
If f(x) is periodic with period T1 and g(x) is periodic with period T2, then f(x) + g(x) is periodic with period equal to l.c.m of T1 and T2, provided there is no positive k such that and .
If f(x) is periodic with period T, then is also periodic with period where and
and are periodic functions with period 2π.
tan x and cot x are periodic functions with period π.
and are periodic functions with period π.
, , and cosecnx are periodic functions with period when n is odd or π when n is even
tann x and cotn x are periodic functions with period π.
|sin x| + |cos x|, |tan x| + |cot x|, |sec x| + |cosec x| are periodic with period .
Ifis a periodic function with period T and g(x) is any function such that domain of domain g, then gof is also periodic with period T.