MATHEMATICAL REASONING
INTRODUCTION
Mathematical Logic is the subject that deals with the methods of reasoning without reference to particular meaning or context. How well the ability to reason can be used depends upon a person’s power to put forward his reasoning. The process of reasoning is especially relevant to deductive mathematics. Logic plays a definitive role in the process of reasoning.
SENTENCE
We communicate our ideas or thoughts with the help of sentences in particular languages. Following types of sentences are normally used :
ASSERTIVE SENTENCE
A sentence that makes an assertion (declaration) is called an assertive or declarative sentence.
Example :
- New Delhi is the Capital of India
- I walk in the morning most every day
IMPERATIVE SENTENCE
A sentence that expresses a request or a command is called an imperative sentence.
Example :
- Please give me a glass of water.
- Go to home.
EXCLAMATORY SENTENCE
A sentence that expresses some strong feeling is called an exclamatory sentence.
Example :
- Hurrah! we have won the match.
- Oh God! what a beautiful scene.
INTERROGATIVE SENTENCE
A sentence that asks some question is called an interrogative sentence.
Example :
- Have you ever gone to Mumbai?
- To which state do you belong?
OPTATIVE SENTENCE
A sentence that expresses a wish is called an optative sentence.
Example :
- God bless you.
- Wish you best of luck.
STATEMENT
A statement (or proposition) is an assertive sentence which is either true or false but not both simultaneously.
Example :
- Natural numbers are always positive.
- Every square is a rectangle.
Each of the above sentences is true, so each of them is a statement.
Example :
- Ratio of two integers is an integer.
- Every rectangle is a square.
Each of the above sentence is false, so each of them is a statement.
Note : A sentence which is both true and false simultaneously is not a statement, rather it is a paradox.
IMPORTANT POINTS
- A true statement is known as a VALID statement
- A false statement is known as an INVALID statement
- A statement cannot be both true as well as false at the same time. This is known as LAW OF EXCLUDED MIDDLE.
- Imperative sentence, Exclamatory sentence, Interrogative sentence, Optative sentence are not statements.
- Mathematical identities are considered to be statements.
OPEN STATEMENT
Let A be a given set. Then a declarative sentence P (x) containing a variable x such that P (x) is true or false for each x A but not both is called an open statement defined on A.
Example :
Sentence (i) x is an integer (ii) ax2 + bx + c = 0
So truth or falsity of sentences depend on the value of the variable x. For some values of a, b and c if x is integer, then the sentence is true, otherwise false. So it is an open statement. The set of all those values of the variable in an open statement for which it becomes a true statement is called the truth set of open statement.
Example :
Open statement : x2 – 3x + 2 = 0, has truth set : {1, 2}.
Truth Value of a Statement : If a statement is true, then its truth value is TRUE or T. If it is false then its truth value is FALSE or F.
Logical Variables : Statements are generally represented by lower case letters such as p, q, r,..... etc. These letters are called logical variables.
SIMPLE STATEMENT
A statement is said to be simple if it cannot be broken into two or more sentences. The truth value of a simple statement does not explicitly depend on any other statement.
For Example :
- Sun rises in the east. Its truth value is T
- ‘Indian Ocean is the biggest ocean’. Its truth value is F
COMPOUND STATEMENT
A statement which is formed by combining two or more simple statements is called a compound statement.
Example :
- These notes are for Mathematics and it targets JEE (Main) and JEE (Advanced).
- If x is a prime number then x cannot be an even number
SUB STATEMENTS
Simple statements which on combining form a compound statement are called sub statements or component statements of the compound statement.
Note : The truth value of compound statement is determined by the truth value of each of its sub statements.
CONNECTIVES
The phrases or words which connect simple statements to form compound statements are called logical connectives or connectives or logical operators. For example, ‘and’, ‘but’, ‘not’, ‘either....or’, ‘neither ....nor’, ‘if ..... then’, ‘..... if and only if .....’ etc.
Joint Denial : The phrases “neither.....nor” connecting two simple sentences is called the joint denial, denoted by 
BASIC LOGICAL OPERATORS
CONJUNCTION
If two simple statements are connected by the word “ and” then the compound statement is called the conjunction of the original statements. We use symbol “∧” to denote the conjunction. If p and q are two simple statements then p ∧q denote the conjunction of p and q and it is read as “ p and q”
Example :
Let p and q be two given statements
p : value of | sin x | is less than 1.
q : the sun rises in the east
p ∧ q : value of | sin x | is less than 1 and the sun rises in the east.
Note:- Symbol ∧ has specific meaning corresponding to connectives, although it may also be used with some other meaning.
Example :
- Ram and Ravi are good friends. “Here ‘and’ is not a connective”.
- Mohan opened the door and ran away. “Here the word ‘and’ is used in the sense of ‘and then’ because the action described in ‘ Mohan ran away’ occurs after the action described in ‘ Mohan open the door’
Normally the conjunction ‘and’ is used between two statements which have some kind of relation but in logic it can be used even if there is no relation between the statements.
Example :
Sun is shining and 5 is an integer.
The truth value of the conjunction p ∧q :
- The statement p ∧q has the truth value T whenever both p and q have the truth value T.
- The statement p ∧q has the truth value F whenever either p or q or both have the truth vale F.
This can be described with the help of following table :
Such a table representing the truth values of a compound statement as dependent on it sub-statement is called a TRUTH TABLE.
Example :
sec x is greater than 1 and tan x is a periodic function. Truth value T
sec x is less than 1 and tan x is a periodic function. Truth value F
sec x is greater than 1 and tan x is not a periodic function. Truth value F
sec x is is less than 1 and tan x is not a periodic function. Truth value F
DISJUNCTION OR ALTERNATION
Two simple statements can be connected by the word “or” to form a compound statement, called the disjunction of the original statements. We use symbol “” to denote disjunction. If p and q are two simple statements then p q denotes the disjunction of p and q and it is read as “ p or q”.
Example :
Let p and q be two given statements
p: Two plus two is four.
q: One is a whole number
p ∨ q : Two plus two is four or one is a whole number.
The truth value of the disjunction p ∨q :
- The statement p ∨ q has the truth value F if both p and q have the truth value F.
- The statement p ∨ q has the truth value T whenever either p or q or both have the truth value T.
Truth table for disjunction is shown below :
Example :
x ≥[x] or |x| ≥ 0 Truth value T
x ≥[x] or |x| < 0 Truth value T
x ≤ [x] or |x| ≥ 0 Truth value T
x ≤ [x] or |x| < 0 Truth value F
Note: - Connective word ‘or’ is also used with different meaning in common language.
Example :
Amit will go to Mumbai or to Bangalore.
It is used in the sense that one or the other possibility exists `but not both so it is not used as a connective.
NEGATION
An assertion that a statement fails or denial of a statement is called the negation of a statement. The negation of a statement is generally formed by introducing the word “ no” at some proper place in the statement or by prefixing the statement with “ it is not the case that” or “ it is false that”. The negation of a statement p is denoted by “~p”.
Example :
A statement:
p : New Delhi is capital of India.
~p : New Delhi is not capital of India.
OR
It is not the case that New Delhi is capital of India.
OR
It is false that New Delhi is capital of India.
If p is a statement and ~ p denote the negation of p then
- ~p has truth value T whenever p has truth value F,
- ~ p has truth value F whenever p has truth value T.
So the truth table for negation is as shown below :
Note:- Negation is called a connective although it does not combine two or more statements. We can say that negation is not a connective but a modifier. It only modifies a given statement and applies only to a single simple statement.
NEGATION OF COMPOUND STATEMENTS
Let p and q are two sub statements.
- Negation of conjunction : The negation of a conjunction p ∧ q is the disjunction of the negation of p and the negation of q. That is
~(p ∧ q) ~p ~ q
Example :
p : Paris is in France.
q : London is in England.
(p ∧ q) : Paris is in France and London is in England.
~ (p ∧ q) : Paris is not in France or London is not in England.
- Negation of Disjunction : The negation of a disjunction p ∨ q is the conjunction of the negation of p and the negation of q. That is
~ (p ∨ q) ~p ∧ ~ q
Example :
p : The earth is the largest planet
q : Ten is a rational number
(p ∨ q) : The earth is the largest planet or ten is a rational number.
~ (p ∧ q). The earth is not the largest planet and ten is not a rational number.
- Negation of a Negation : Negation of negation of a statement is the statement itself i.e. ~ (~ p) p.
Example :
p: Sky is blue
~p: Sky is not blue.
~(~p) : It is not the case that sky is not blue.
OR
It is false that sky is not blue
OR
Sky is blue.
IMPLICATION OR CONDITIONAL STATEMENTS
Two statements, when connected by the phrase ‘if........then’ give a compound statement known as an implication or a conditional statement.
If p and q are two statements then it is denoted by “ p→ q” or “ p ⇒ q” and read as “p implies q”. Here p is called antecedent and q is the consequent.
For Example :
p : ABC is a triangle.
q : AB + BC >AC.
p ⇒ q : If ABC is a triangle then AB + BC >AC.
The Truth value of the implication p ⇒ q
- The statement p ⇒ q has the truth value F if p has truth value T and q has truth F.
- The statement p ⇒ q has the truth value T if either p and q both have truth value F or q has truth value T. This has been shown in the following truth table.
p ⇒ q can be read in any one of the following ways :
(i) if p then q
(ii) p implies q
(iii) p only if q
(iv) q if p
(v) p is sufficient condition for q
(vi) q is necessary condition for p
CONVERSE, INVERSE AND CONTRAPOSITIVE OF AN IMPLICATION
If p and q are two statements, then
Implication: p ⇒ q
Converse: q ⇒ p
Inverse: ~ p ⇒ ~ q.
Contrapositive: ~ q ⇒ ~ p
BICONDITIONAL OR EQUIVALENCE STATEMENT
Two simple statements connected by the phrase “if and only if” give a biconditional statement. It is the conjunction of the conditional statements, one converse to the other. If p and q are two statements then biconditional statement is denoted by
“p ⇔ q” or “p q” so that
“p ⇔ q” or “p q” so that
p ⇔ q: (p ⇒ q) ∧ (p ⇒ q)
For example :
p: A number is divisible by 3.
q: The sum of the digits forming the number is divisible by 3.
p ⇔ q: A number is divisible by 3 if and only if the sum of the digits forming the number is divisible by 3.
The truth value of the biconditional statement p ⇔ q :
- The statement p ⇔ q has the truth value T if both the statements p and q have the same truth value.
- The statement p ⇔ q has the truth value F if exactly one of the statements has truth value T and the other has truth value F.
The corresponding truth table is as follows
NEGATION OF CONDITIONAL STATEMENT
- Negation of Implication
The negation of an implication p ⇒q is the conjunction of p and the negation of q
i.e. ~( p ⇒ q)  p ∧ ~q.
p ∧ ~q.
For Example :
p: It is raining.
q: The school is closed.
~q: The school is not closed.
p ⇒ q: If it is raining, then the school is closed.
~(p ⇒ q): It is raining and the school is not closed.
- Negation of Biconditional Statement
The negation of equivalence pq is disjunction of the negation of implication p ⇒ q and the negation of implication q ⇒ p. That is
~ (p  q)
q) 
 (p ∧ ~ q ) ∨ (q ∧ ~ p)
(p ∧ ~ q ) ∨ (q ∧ ~ p)
PROPOSITION
A compound statement having component statements p, q, r, .... etc. with repetitive use of the connectives ∧,∨, ⇒, ⇔ and ~ is called a proposition (or a statement form or a statement pattern or a well formed formula.
Example :
~ p ⇒ q, pv ~q, (p ⇒q) ∧ (q ⇒p), ~ (p ⇒q) are some proposition.
In a statement pattern, when brackets are not given, we decide priority for the connectives in the following order:
(i) ~ (ii) ∧ (iii) ∨ (iv) ⇒ (v) ⇔
TAUTOLOGIES (OR THEOREM)
A proposition is said to be a tautology if it is true for all logical possibilities. In other words a statement is called tautology if its truth value is T and only T.
Example : Consider the proposition p ~p. Its truth table is as follows.
We see that truth value of p ∨ ~p is always T. So it is a tautology.
CONTRADICTIONS (OR FALLACY)
A proposition is said to be contradiction if it is false for all logical possibilities. In other words a statement is called contradiction if its truth value is F and only F.
Example : Consider the statement p ∧ ~p. Its truth table is shown below:
We see that truth value of p ∧ ~p is always F. So it is a contradiction.
CONTINGENCY
A proposition is said to be contingency if it is either true or false depending on truth value of its components. Clearly a contingency is a statement form which is neither a tautology nor a contraction.
The negation of a tautology is a contradiction and vice versa.
LOGICAL EQUIVALENCE
Two statement S1(p, q, r,....) and S2 (p, q, r,.......) are said to be logically equivalent if they have the same truth value for all logical possibilities and it is denoted by
S1(p, q, r,.......) S2 (p, q, r,.....)
S2 (p, q, r,.....)
S1 and S2 are logically equivalent if they have identical truth tables (means entries in the last column of the truth tables are the same).
Alternatively the statements, S1 and S2 are logically equivalent if S1 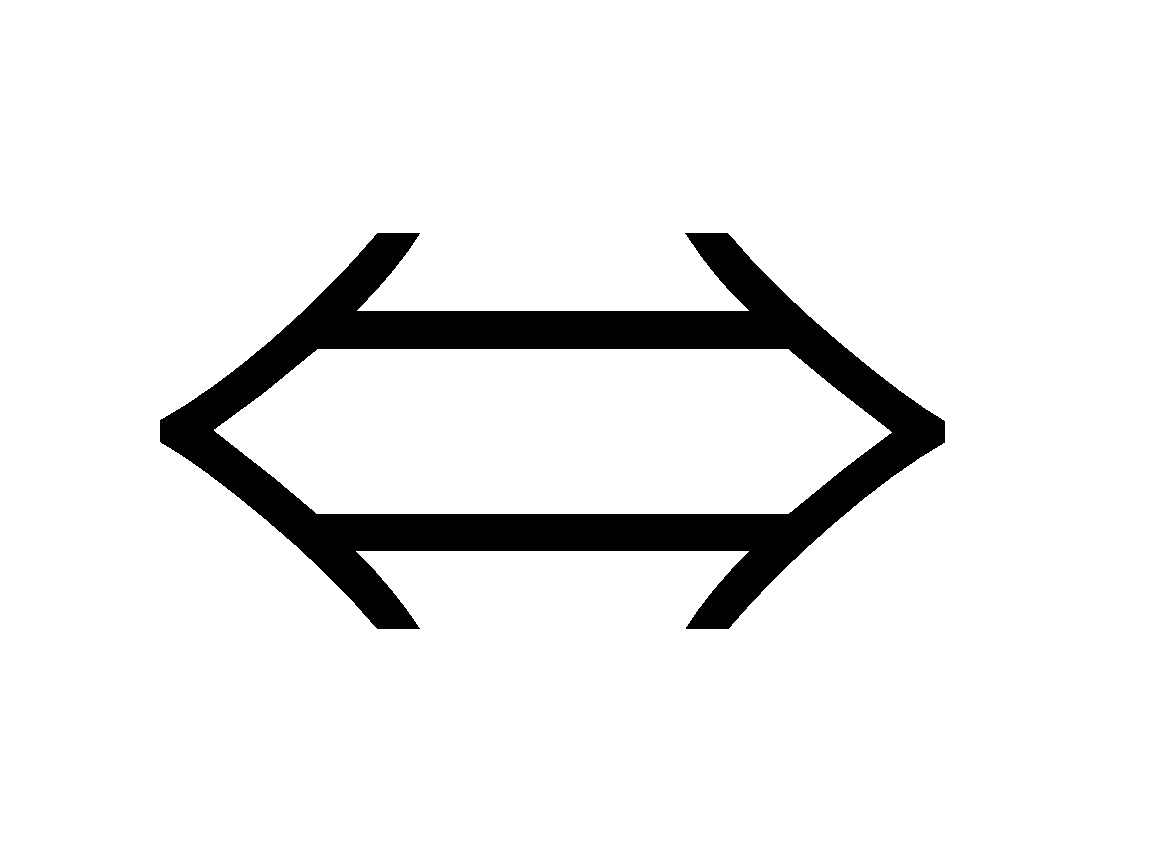 S2 is a tautology.
S2 is a tautology.
DUALITY
Two compound statements S1 and S2 are said to be duals of each other if one can be obtained from the other by replacing ∧ by ∨ and ∨ by ∧.
Note :
- The connective ∧ and ∨ are also called duals of each other.
- If a compound statement contains the special variable t(tautology) or c (contradiction), then to obtain its dual we replace t by c and c by t in addition to replacing ∧ by ∨ and ∨ by ∧.
- Let S(p, q) be a compound statement containing two sub statements and S* (p, q) be its dual. Then,
- ~ S(p, q)
s* (~ p, ~ q)
- ~S* (p, q)
S(~p, ~ q)
- The above result can be extended to the compound statements having finite number of sub-statements. Thus, if S (p1, p2, .....pn) is a compound statement containing n sub-statement p1, p2, ....., pn and S* (~p1, p2,......, pn) is its dual. Then,
- ~ S (p1, p2, ......., pn)
S* (~ p1, ~p2, ........, ~pn)
- ~S* (p1, p2, ......., pn)
S (~p1, ~ p2, ........, ~pn)
ALGEBRA OF STATEMENTS
- Idempotent laws : For any statement p, we have
- Commutative laws : For any two statements p and q, we have
- Association laws : For any three statements p, q, r, we have
- Distributive laws : For any three statements p, q, r we have
- Demorgan’s laws : If p and q are two statements, then
- Identity laws : If t and c denote a tautology and a contradiction respectively, then for any statement p, we have
- Complement laws : For any statements p, we have
- ~t = c
- ~c = t
where t and c denote a tautology and a contradiction respectively.
- Law of contrapositive : For any two statements p and q, we have
- Involution laws : For any statement p, we have







