Matrices | Mathematics Notes for IITJEE Main

MATRICES

A set of mn numbers (real of imaginary) arranged in the form of a rectangular array of m rows and n columns is called an m × n matrix [to be read as 'm by n' matrix]. An m × n matrix is usually written as

In a compact form the above matrix is represented by A =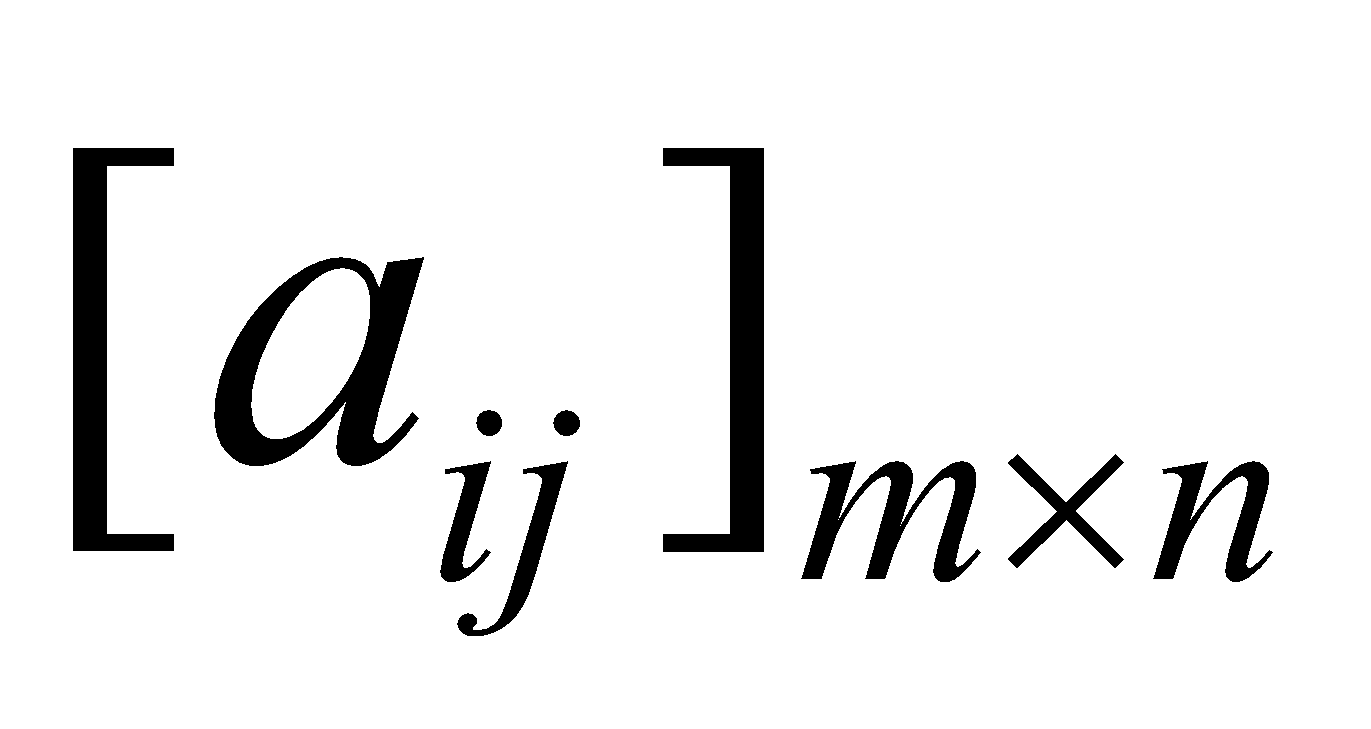

The numbers a11, a12.... etc. are called the elements of the matrix. The element aij belongs to ith row and jth column and is called the (i, j)th element of the matrix A = [aij]. Thus, in the element aij the first subscript 'i' always denotes the number of row and the second subscript 'j', the number of column in which the element occurs.

TYPES OF MATRICES

ROW MATRIX

A matrix having only one row is called a row matrix or a row vector.

For example, A = [2  7 –8 5 4]1×5 is a row matrix of the order 1 × 5.

COLUMN MATRIX

A matrix having a single column is called a column matrix.

For example, A =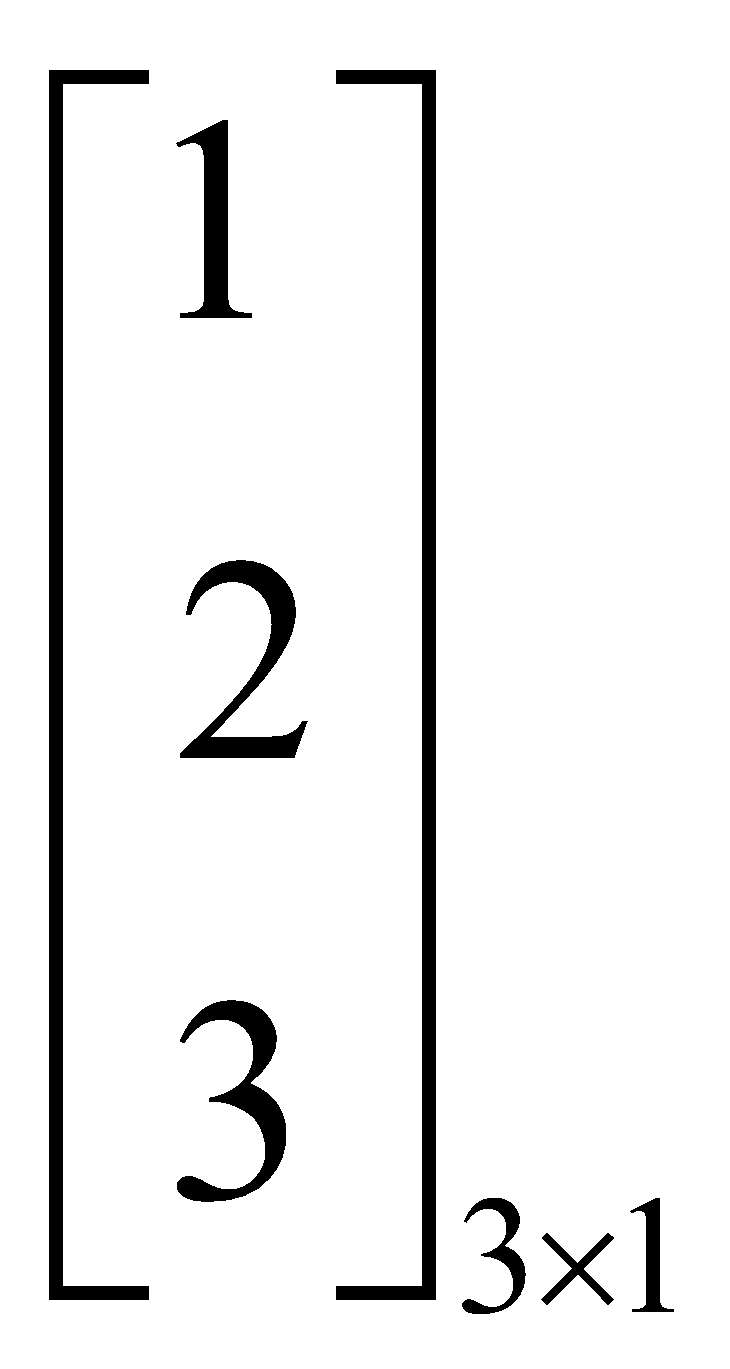

NULL MATRIX

A matrix whose all elements are zero is called a null matrix and is denoted by O.

For example,  and  are null matrices.

SQUARE MATRIX

A matrix in which the number of rows is equal to the number of columns, say n, is called a square matrix of order n. A square matrix of order 'n' is also called an 'n-rowed square matrix'.

The elements aij of a square matrix A = [aij] n×n for which i = j, i.e., the elements a11, a22 ...., ann are called the DIAGONAL ELEMENTS and the line along which they lie is called the PRINCIPAL DIAGONAL of the matrix.

Let us consider the matrix

This is a square matrix of order 4. The elements 1, 3, 4, 4 constitute the principal diagonal of this matrix. The sum of the diagonal elements of a square matrix A is called the TRACE of A, denoted by tr(A). For the above matrix tr(A) = 1 + 3 + 4 + 4 = 12

DIAGONAL MATRIX

A square matrix A = [aij]n×n is called a diagonal matrix if all the elements, except those in the leading diagonal, are zero, i.e., aij = 0 . A diagonal matrix of order n × n where diagonal elements are d1, d2 ..... dn is denoted by diag (d1, d2, ....dn).

The matrix  is a diagonal matrix.

SCALAR MATRIX

A square matrix A = [aij]n×n is called a scalar matrix if

(i)   and (ii) , where c is a non-zero real number

In other words, a diagonal matrix in which all the elements in the leading diagonal are equal is called a scalar matrix, e.g.

IDENTITY MATRIX

A square matrix A = [aij]n×n is called a unit matrix or an identity matrix if

(i)              (ii)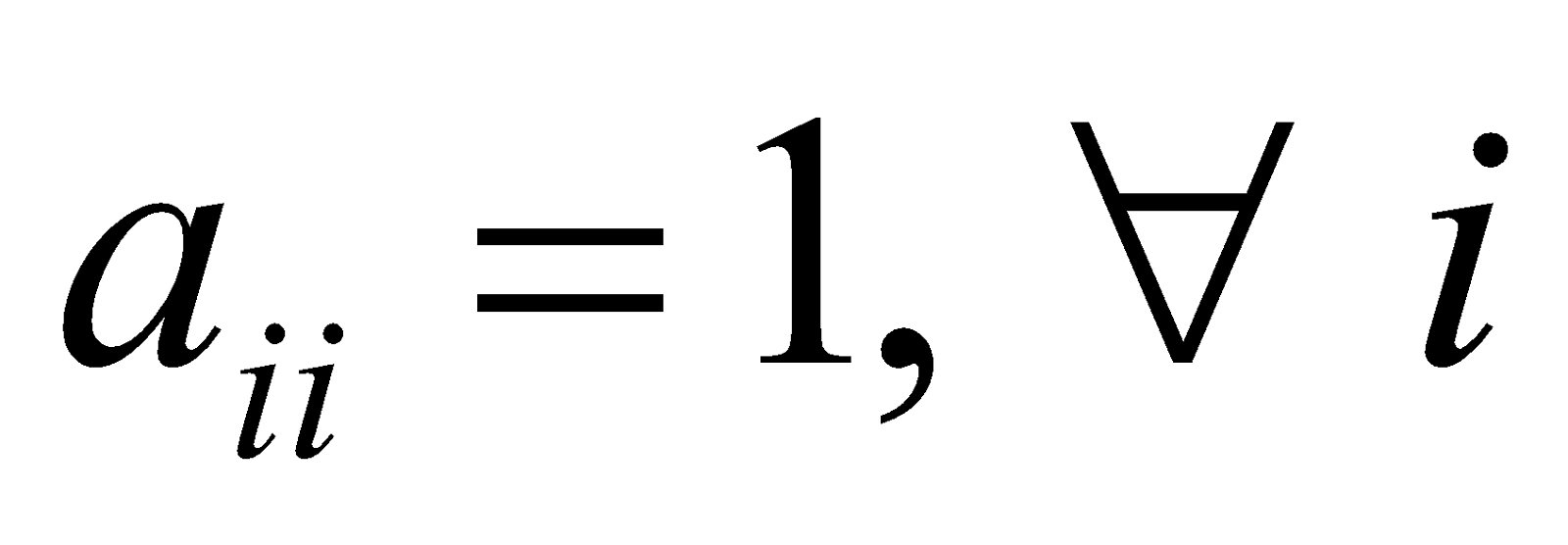

In other words, a square matrix each of whose diagonal elements is 1 and each of whose non-diagonal elements is equal to zero is called a unit matrix or an identity matrix. The identity matrix of order 'n' is denoted by 'In'. Thus

are unit matrices of orders 2 and 3 respectively.

UPPER TRIANGULAR MATRIX

A square matrix A = [aij] is called an upper triangular matrix if aij = 0 for all i > j. Thus, in an upper triangular matrix all the elements below the principal diagonal are zero.

For example, A = is an upper triangular matrix.

LOWER TRIANGULAR MATRIX

A square matrix A = [aij] is called a lower triangular matrix if aij = 0 for all i < j. Thus in a lower triangular matrix all the elements above the leading diagonal are zero.

A triangular matrix A = [aij]n×n is called a strictly triangular if aii = 0 for i = 1, 2, .... n.

SUB-MATRIX

A matrix which is obtained from a given matrix by deleting any number of rows or columns or both is called a sub-matrix of the given matrix. For example,

 is a sub-matrix of the matrix .

Obtained by deleting first row and first column.

EQUALITY OF TWO MATRICES

Two matrices A = [aij] and B = [bij] are said to be equal if

(i)  They are of the same order and (ii)  aij = bij for all i, j.

If two matrices A and B are equal, we write A = B, otherwise we write A ≠ B.

ADDITION OF MATRICES

Let A = [aij], B = [bij] be two matrices of the same order m × n. Then their sum A + B is defined to be the matrix of the order m × n such that (A + B)ij = aij + bij for all i, j. For example, if

and , then

REMARK : It should be noted that the addition is defined only for matrices of the same order.

PROPERTIES OF MATRIX ADDITION

• Matrix addition is commutative : If A and B be two m × n matrices, then A + B = B + A
• Matrix addition is associative : If A, B and C be three m × n matrices, then
• Existence of Additive Identity : The null matrix is the identity for matrix addition, i.e., A + O = A = O + A for every matrix A.
• Existence of Additive Inverse : For every matrix A = [aij]m × n there exists a matrix [–aij]m×n denoted by –A such that

The matrix is called the additive inverse of . If A and B are two m×n matrices, then we define

Thus, A – B, called subtraction of B from A, is obtained by subtracting from each element of A, the corresponding elements of B.

• Cancellation laws hold well in case of addition of matrices : If A, B, C are three m×n matrices, then

(Left Cancellation Law)

and (Right Cancellation Law)

MULTIPLICATION OF A MATRIX BY A SCALAR

Let A = [aij]m×n be an m×n matrix and k be any number called a scalar. The matrix obtained by multiplying every element of A by k is called the scalar multiple of A by k and is denoted by kA. Thus,

For example, if , then 3A =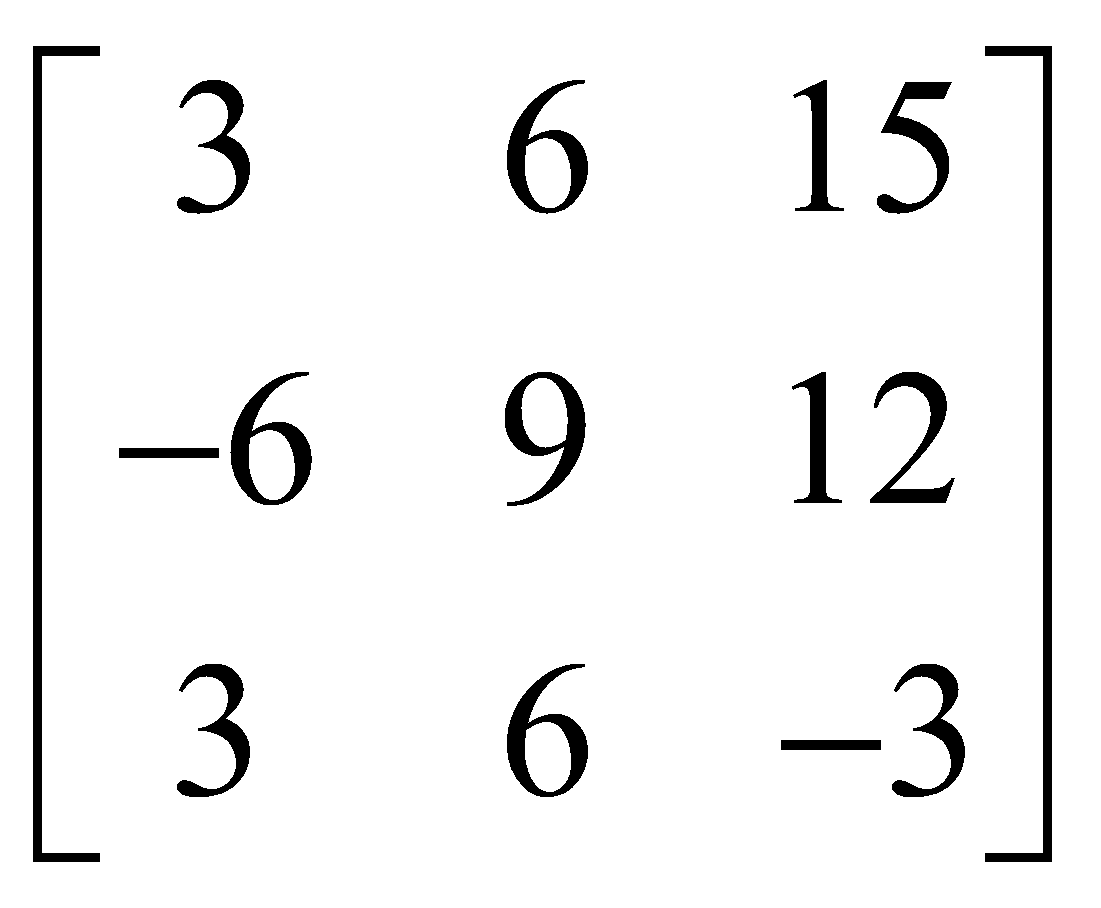

PROPERTIES OF SCALAR MULTIPLICATION

If ,   are two matrices and k, l are scalars, then

• 
• (k + l)A = kA + lA
• (–k)A = –(kA) = k(–A)
• k(lA) = (kl) A = l (kA)
• 1 A = A
• (–1) A = –A

MULTIPLICATION OF TWO MATRICES

Let A, B be two matrices. Then they are conformable for the product AB if the number of columns in A (pre-multiplier) is the same as the number of rows in B (post-multiplier). Thus, if
A =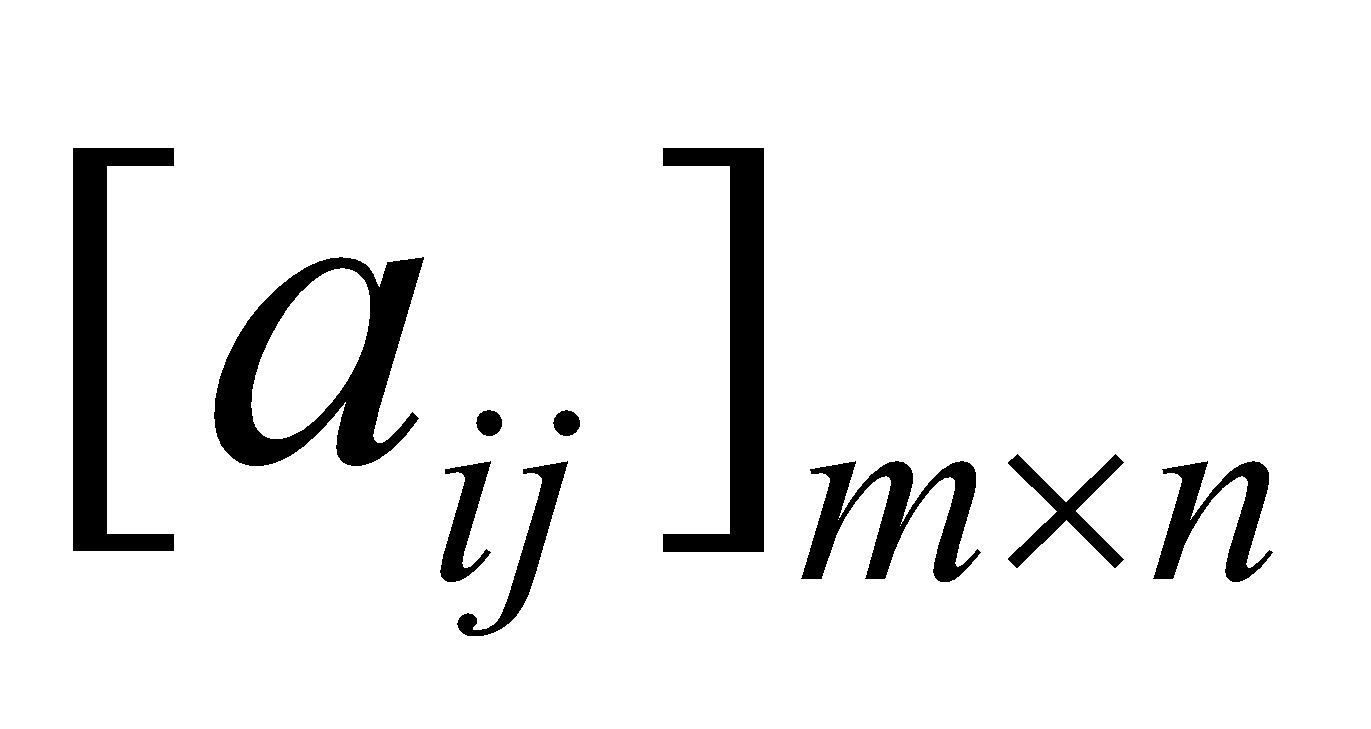 , B = are two matrices, then their product AB is a matrix of order m × p and is defined as

                      

For example, if , then A and B are conformable for the product AB such that, 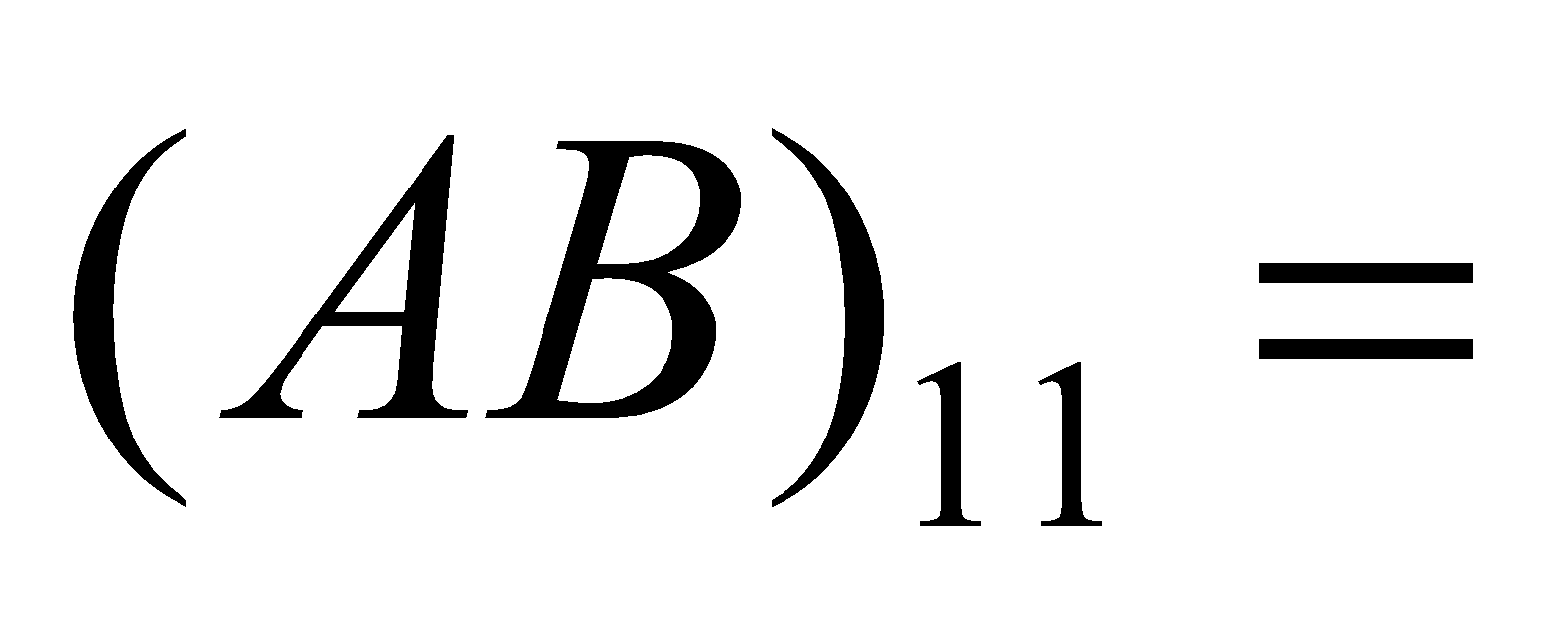 (First row of A) (First column of B) =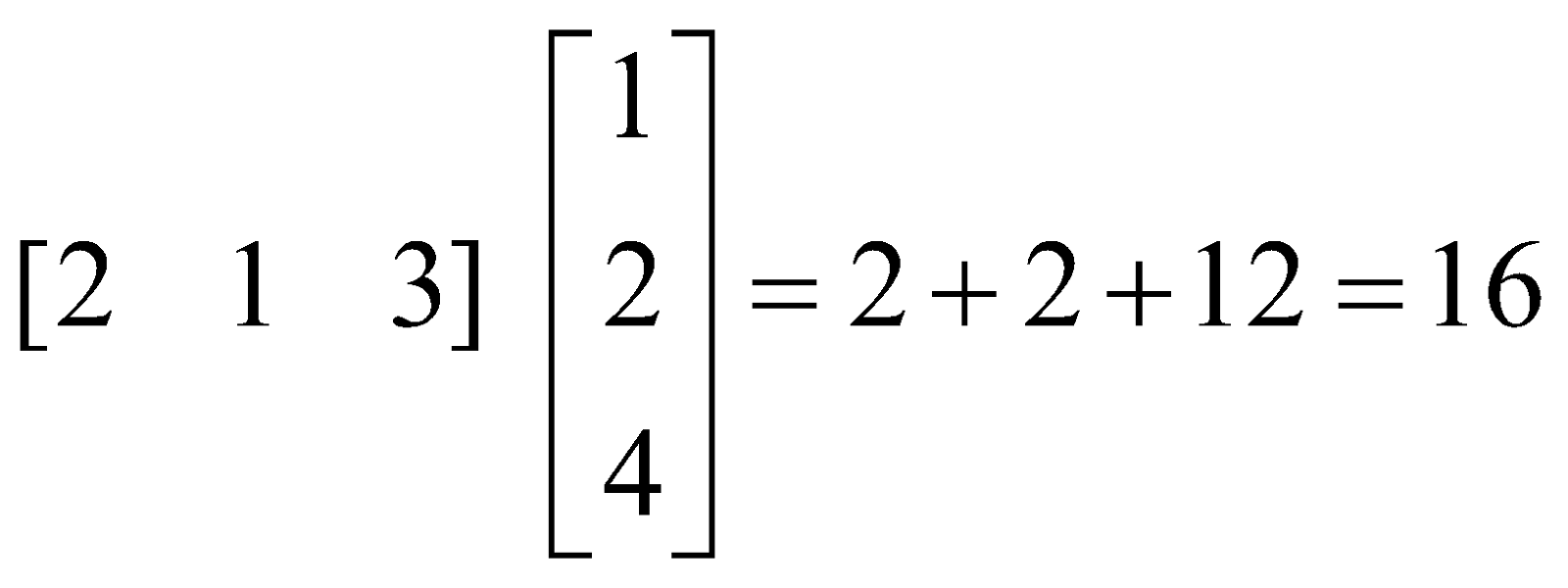

(First row of A) (Second column of B)

      = . etc.

Thus, AB =

PROPERTIES OF MATRIX MULTIPLICATION

• Matrix multiplication is associative, i.e., if A, B, C are m × n, n × p and p × q matrices respectively, then (AB) C = A (BC)
• Matrix multiplication is not necessarily commutative.
• Matrix multiplication is distributive over matrix addition, i.e.  (B + C) = AB + AC, where A, B, C are any three, m × n, n × p, n × p matrices respectively.
• The product of two matrices can be the null matrix while neither of them is the null matrix. For example,

If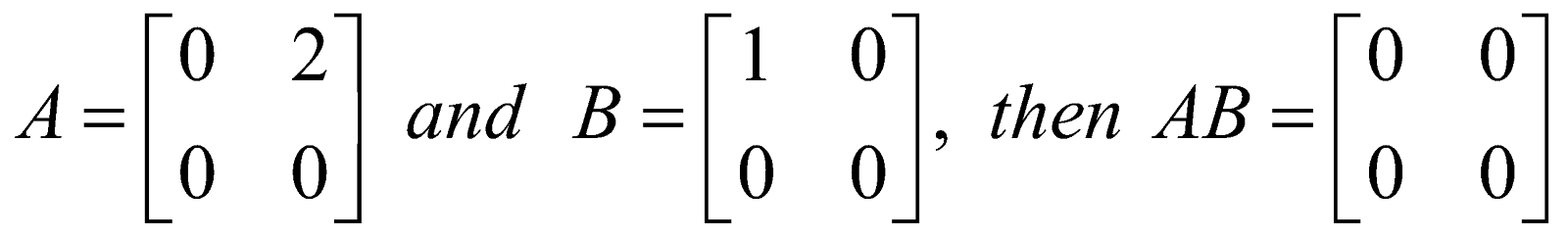

• If A is an m × n matrix, then .

POSITIVE INTEGRAL POWERS OF MATRICES

If A is any matrix, then the product AA is defined only if A is a square matrix. We denote this product AA by A2.

Now, by the Associative Law,

.

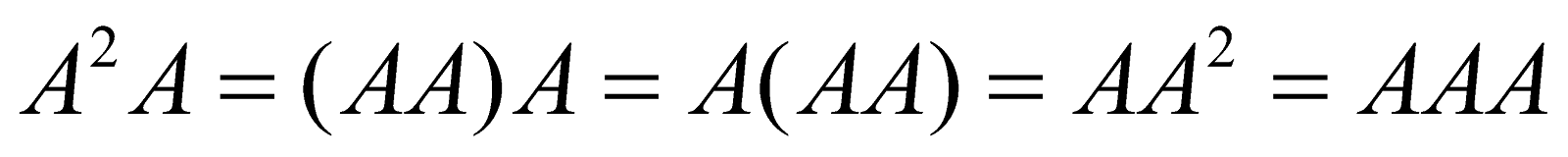
We denote this product by A3.

Similarly, for any number of square matrices, we define AAA ..... n times = An.

NOTE :

1. If I is a unit matrix of any order then

2. Consider any polynomial in x

, we define for any square matrix A.

f(A) is called a matrix polynomial.

NILPOTENT MATRIX

A square matrix A is said to be nilpotent matrix if there exists a positive integer m such that Am = 0. If m is the least positive integer such that Am = 0, then m is called the index of the nilpotent matrix A.

For example, if A = , then

A2 = AA = = 0

Hence the matrix A is nilpotent of the index 2.

IDEMPOTENT MATRIX

A square matrix A is called an idempotent matrix if A2 = A.

INVOLUTORY MATRIX

A square matrix A is said to be involutory matrix if A2 = 1.

For example, if A = , then

A2 = 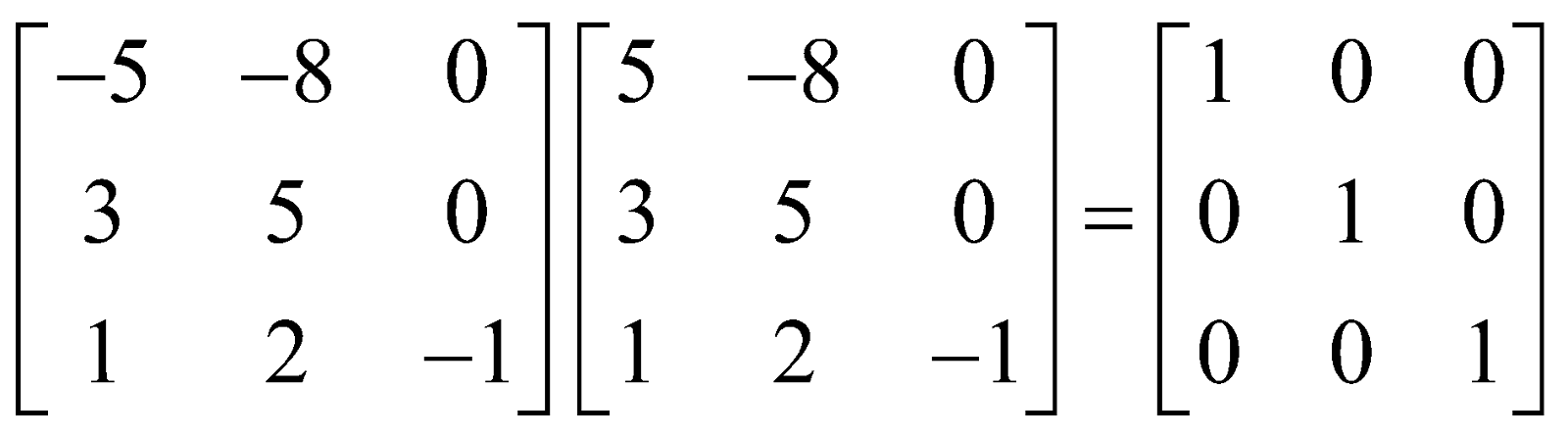= I

Hence A is involutory.

TRANSPOSE OF A MATRIX

Let A = [aij] be an m × n matrix. Then the transpose of A denoted by AT or A' is an n × m matrix such that (AT)ij = aji for all i = 1, 2, 3, ....., m; j = 1, 2, ....., n.

Thus, AT is obtained from A by changing its rows into columns and columns into rows.

For example, if A = , then

PROPERTIES OF TRANSPOSE

Let A, B be two matrices, then

1. 
2. , A and B being of the same order.
3. , k being a scalar.
4. and B being conformable for multiplication.

SYMMETRIC AND SKEW-SYMMETRIC MATRICES

SYMMETRIC MATRIX

A square matrix  is called a symmetric matrix if  for all i, j.  

for all  i, j.

For example,  is a symmetric matrix.

SKEW-SYMMETRIC MATRIX

A square matrix A = [aij] is called a skew-symmetric matrix

If 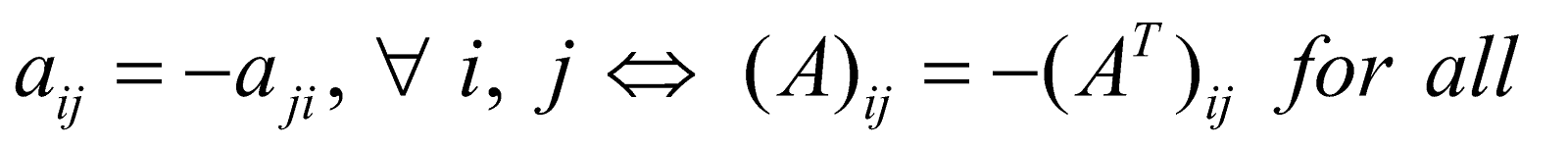i, j

If  is a skew-symmetric matrix, then

for all i, j  for all i  for all i for all i.

Thus the diagonal elements of a skew-symmetric matrix are all zero.

For example, the matrix  is a skew-symmetric matrix.

THEOREM

"Every square matrix can be uniquely expressed as the sum of a symmetric and a skew-symmetric matrix."

Let A be a square matrix.

Then,

where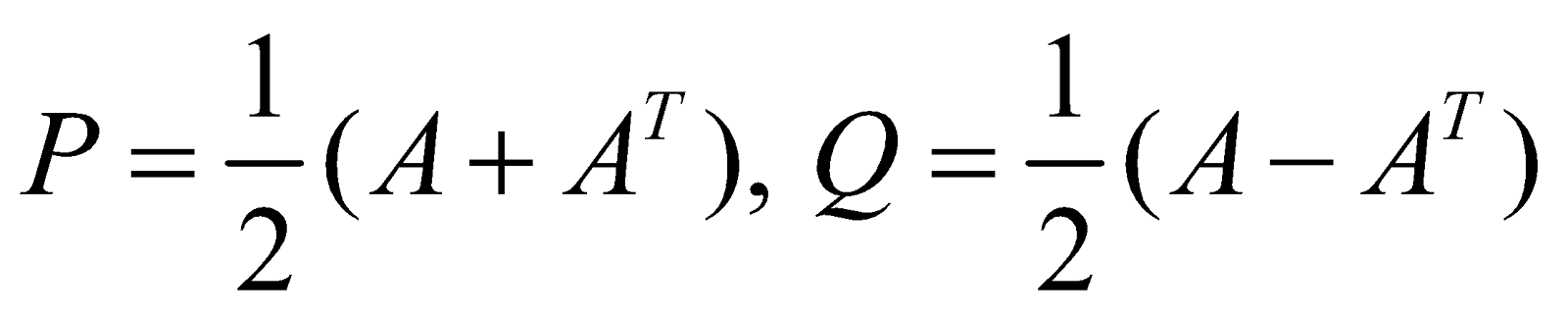  

now,  

       

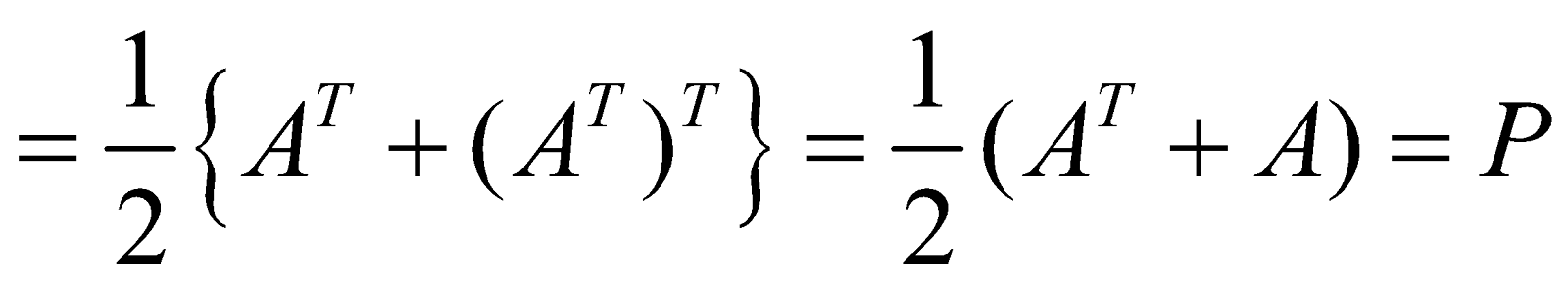
And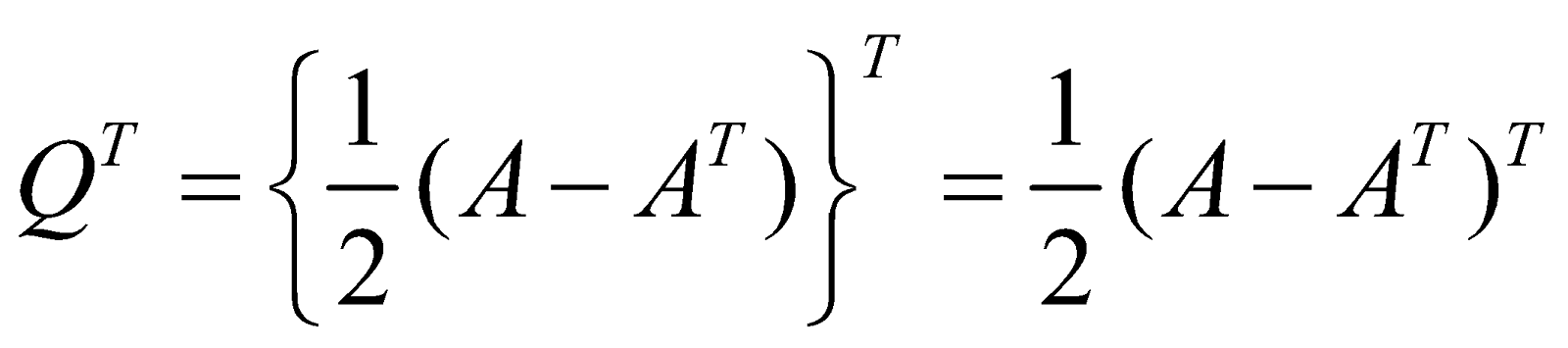  

is symmetric and Q is skew-symmetric.

Thus, A can be expressed as the sum of a symmetric and a skew-symmetric matrix.

IMPORTANT PROPERTIES

1. If A is a square matrix, then
1. A + AT is symmetric
2. A – AT is skew-symmetric
2. If A and B are two symmetric (or skew-symmetric) matrices of the same order, then so is A + B
3. If A is symmetric (or skew-symmetric) matrix and k is a scalar, then kA is also symmetric (or skew-symmetric).
4. If A and B are symmetric matrices of the same order, then the product AB is symmetric if and only if AB = BA.
5. The matrix BTAB is symmetric or skew-symmetric according as A is symmetric or skew-symmetric.
6. All positive integral powers of a symmetric matrix are symmetric.
7. All positive odd integral powers of a skew-symmetric matrix are skew-symmetric and positive even integral powers of a skew-symmetric matrix are symmetric.
8. If A and B are symmetric matrices of the same order, then
1. AB – BA is a skew-symmetric matrix
2. AB + BA is a symmetric matrix.

DETERMINANT OF A MATRIX

Every square matrix can be associated to a unique number, which is called its determinant. The determinant of a square matrix A is denoted by | A | or det (A).

If  A = , then determinant of A is

  etc. (see determinants)

SINGULAR MATRIX

A square matrix A is called a singular matrix if determinant of , otherwise A is called a non-singular matrix.

MINORS AND COFACTORS OF SQUARE MATRIX

MINOR

Let A = [aij] be an n-rowed square matrix. Then the minor Mij of aij is the determinant of the sub matrix obtained by leaving ith row and jth column of A.

For example, if  then

COFACTOR

Let A = [aij] be an n-rowed square matrix. Then the cofactor Aij of aij is equal to (–1)i + j times the minor Mij of aij, i.e. .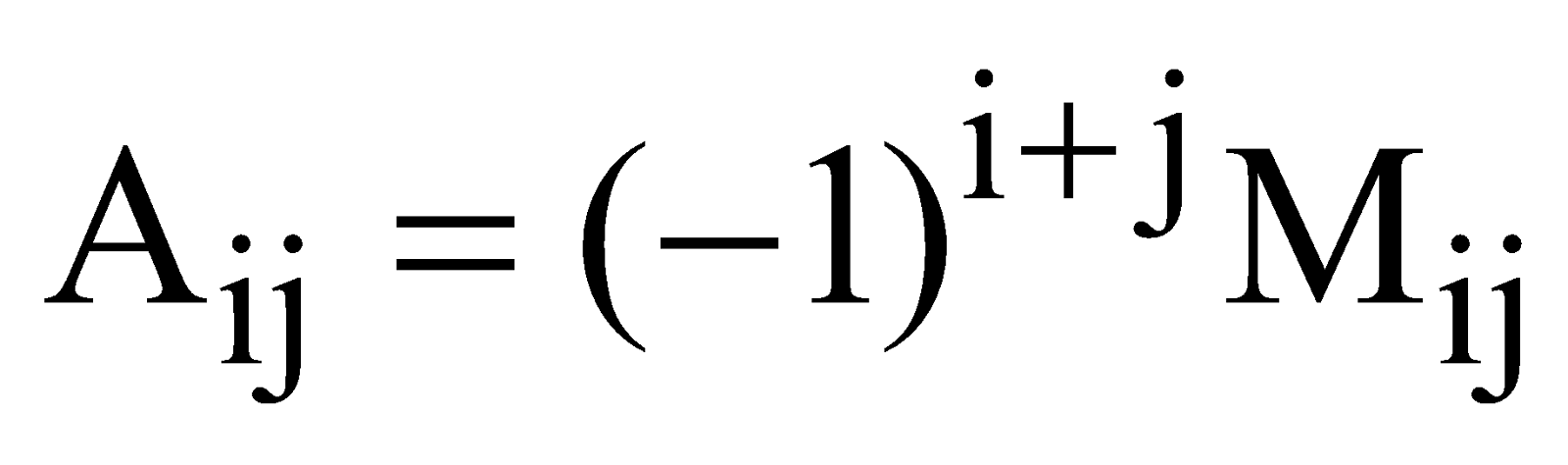

ADJOINT OF A SQUARE MATRIX

Let A = [aij] be square matrix of order n × n, and Aij be the cofactor of aij in A. Then the transpose of the matrix of cofactors of elements in A is called the adjoint of A and is denoted by adj A.

Thus,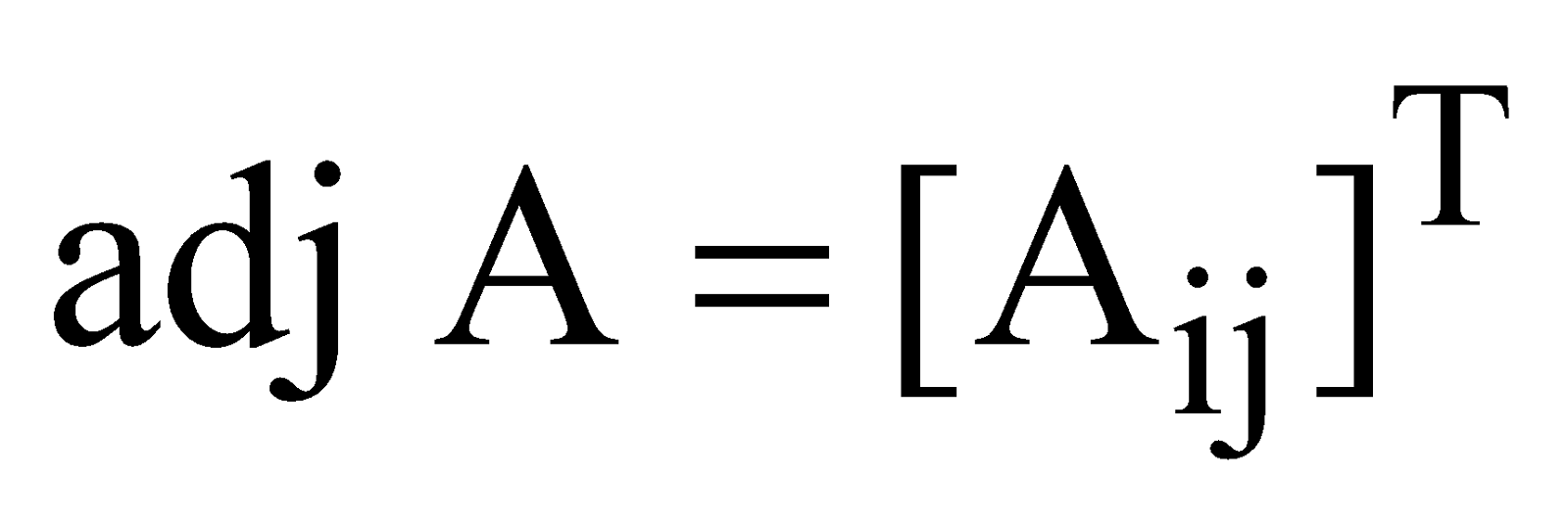

= cofactor of aji in A.

PROPERTIES OF THE ADJOINT OF A MATRIX

1. If A is a square matrix of order n, then

A (adj A) = | A | In = (adj A)A

where In is a square matrix of order n.

Also | adj A | = | A |n–1

2. If A is a square matrix of order n, then

adj (AT) = (adj A)T.

3. If A and B are two square matrices of the same order, then adj (AB) = (adj B) (adj A)
4. adj (adj A) = |A|n–2 A, where A is a non-singular matrix.
5. |adj (adj A)| = , where A is a non-singular matrix.
6. Adjoint of a diagonal matrix is a diagonal matrix.

INVERSE OF A MATRIX

Let A be a square matrix of order n. Then a matrix B is called inverse of A if AB = In = BA

The inverse of A is denoted by A–1.

THEOREM

A square matrix A is invertible if and only if it is non-singular.

PROOF : Let A be a square matrix of order n. Let A be an invertible matrix. then there exists a matrix B such that

is a non-singular matrix.

Conversely, let A be an n × n non-singular matrix. Then A(adj A) = | A | In = (adj A) A

A is invertible such that .

THEOREMS

1. Inverse of a square matrix, if it exists, is unique.
2. If A, B are two invertible matrices of the same order, then AB is invertible and
3. Let A, B, C be invertible matrices of the same order, then ABC is invertible and
4. If A is a n-rowed non-singular matrix, then
5. The inverse of the inverse is the original matrix itself, i.e. (A–1)–1 = A.
6. Let A, B, C be square matrices of the same order n. If A is a non-singular matrix, then

AB = AC ⇒ B = C (Left cancellation law)

BA = CA ⇒ B = C (Right cancellation law)

Note that these cancellation laws hold only if the matrix A is non-singular.

7. If A is a non-singular matrix such that A is symmetric then A–1 is also symmetric.
8. If A is a non-singular matrix, then |A–1| = |A|–1.

ORTHOGONAL MATRIX

A square matrix A is called an orthogonal matrix if . If A is an orthogonal matrix then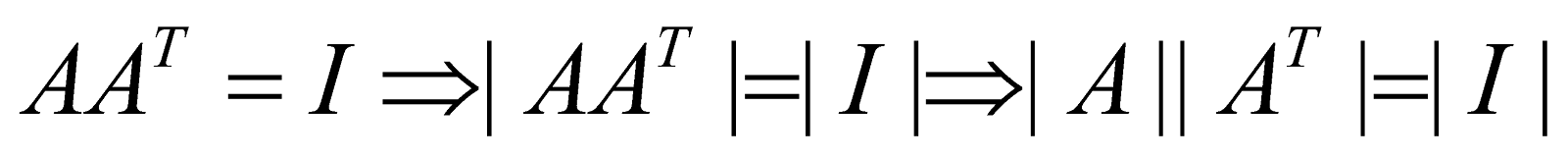

Thus, every orthogonal matrix is non-singular.

Consequently every orthogonal matrix is invertible.

Result :

• If A, B be n-rowed orthogonal matrices, then AB and BA are also orthogonal matrices.
• If A is an orthogonal matrix, then AT and A–1 are also orthogonal.

ELEMENTARY OPERATION (TRANSFORMATION) OF A MATRIX

There are six operations (transformations) on a matrix, three of which are due to rows and three due to columns, which are known as elementary operations or transformations.

1. The interchange of any two rows or two columns. Symbolically the interchange of ith and jth rows is denoted byand interchange of ith and jth column is denoted by

For example, 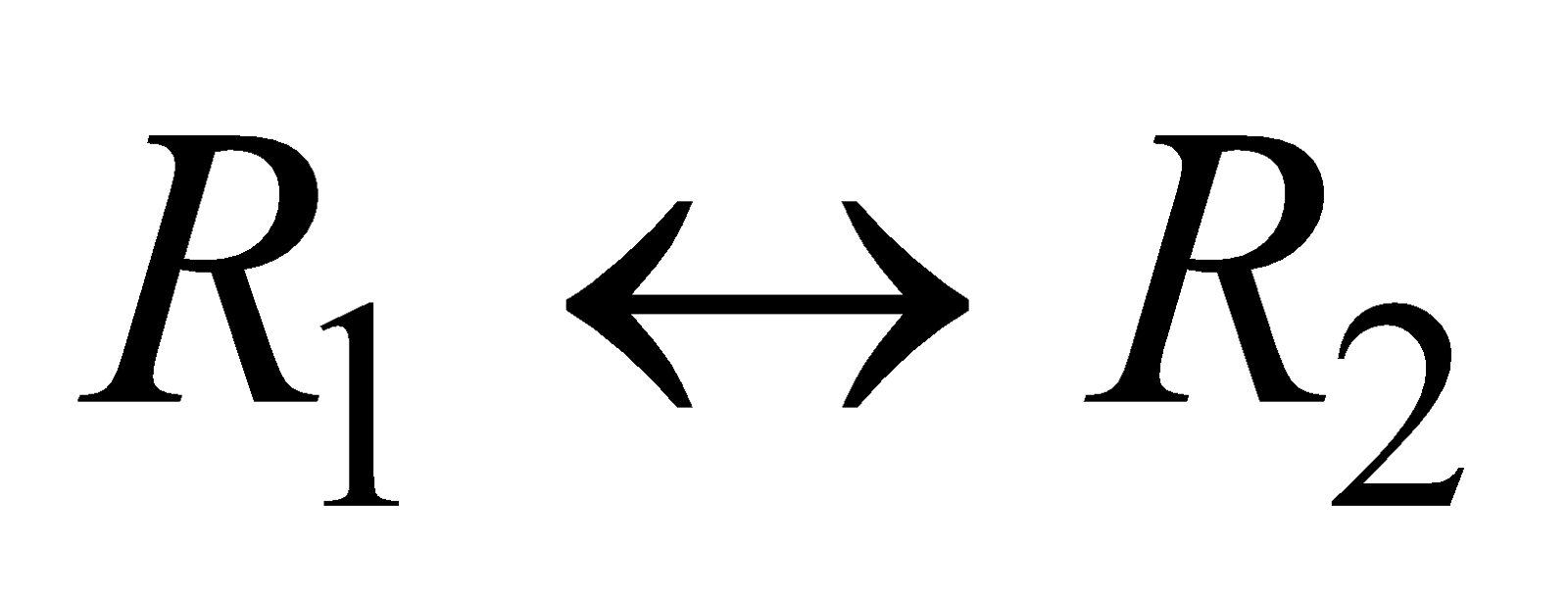applying to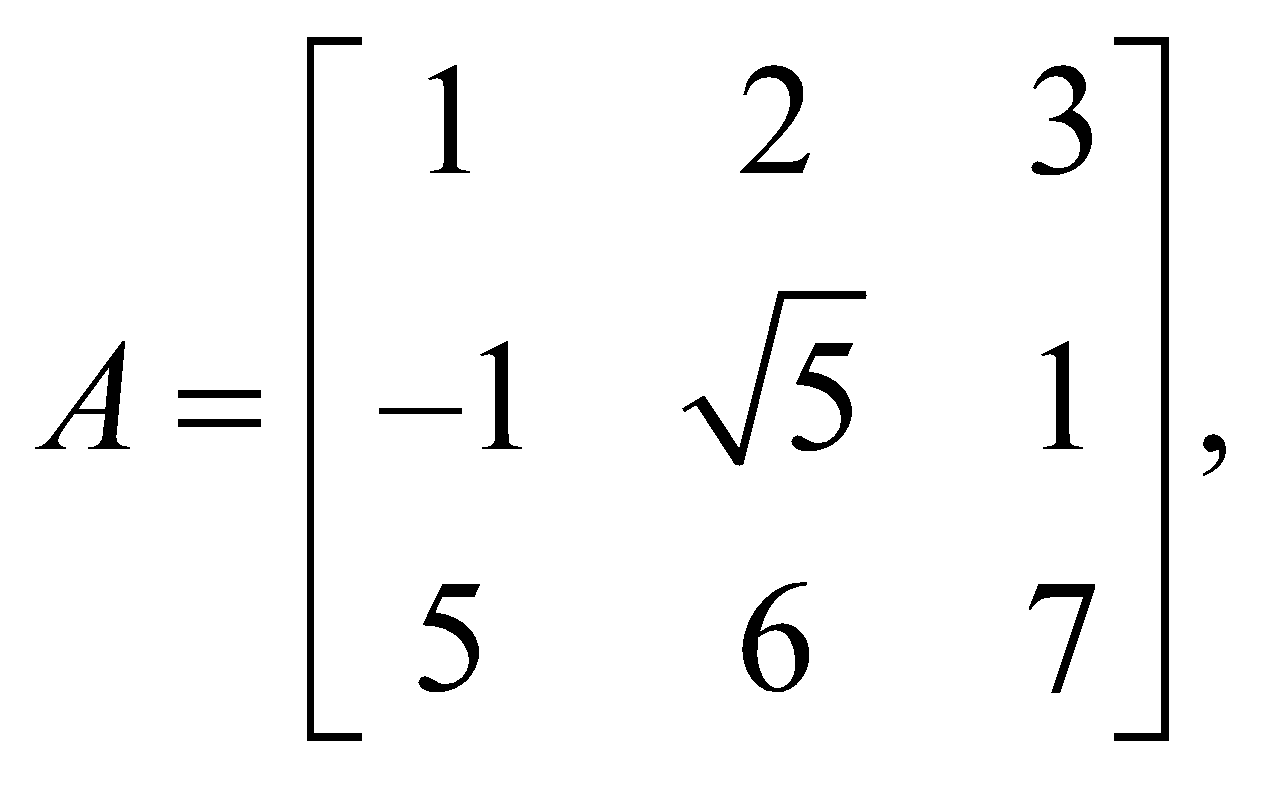

we get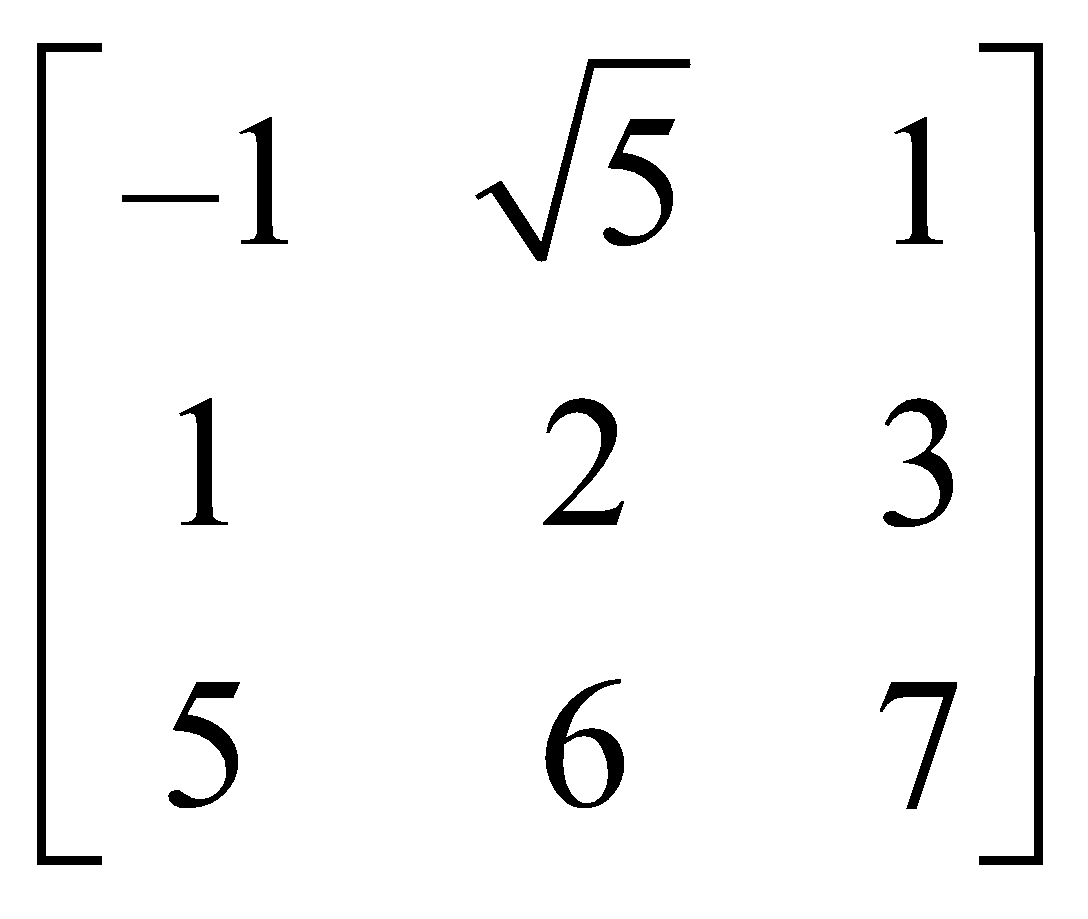

2. The multiplication of the elements of any row or column by a non zero number. Symbolically, the multiplication of each element of the ith row by k, where k ≠ 0 is denoted by Ri → kRj

The corresponding column operation of denoted by Ci → kCj

For example, 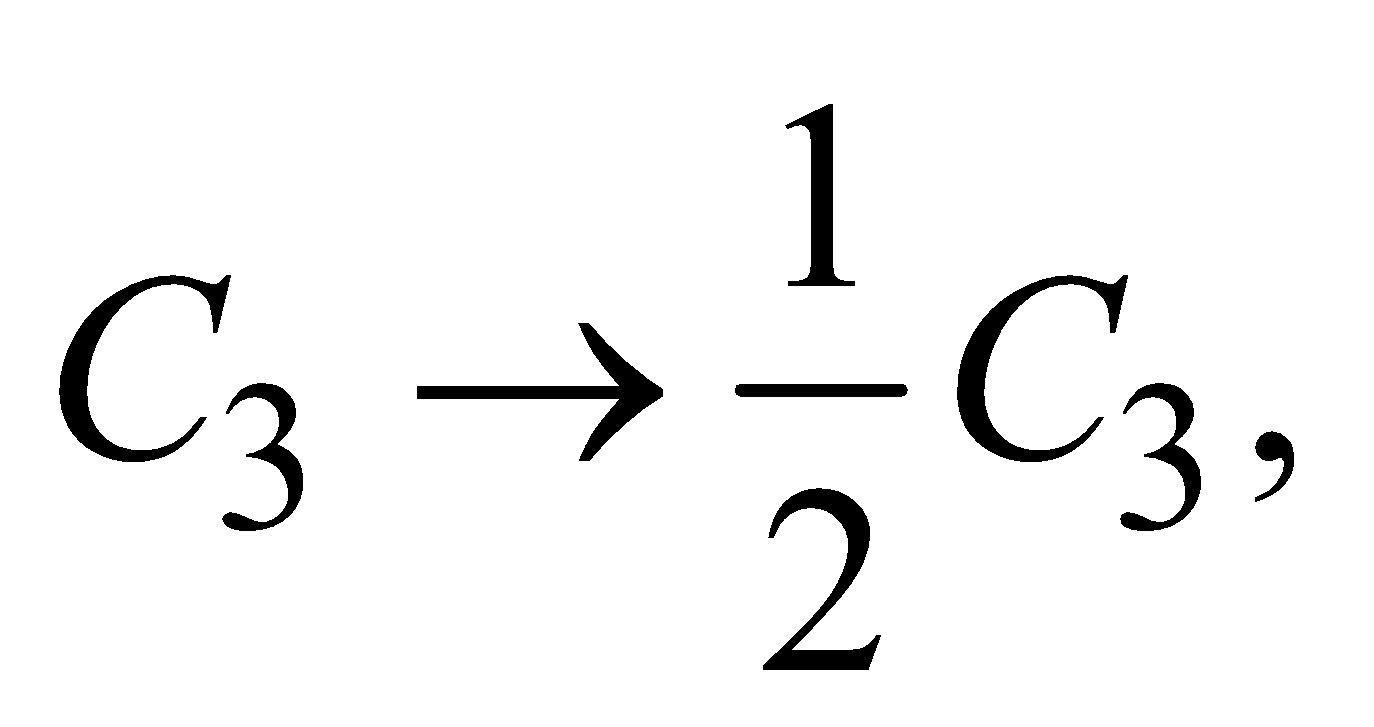applying to B =we get

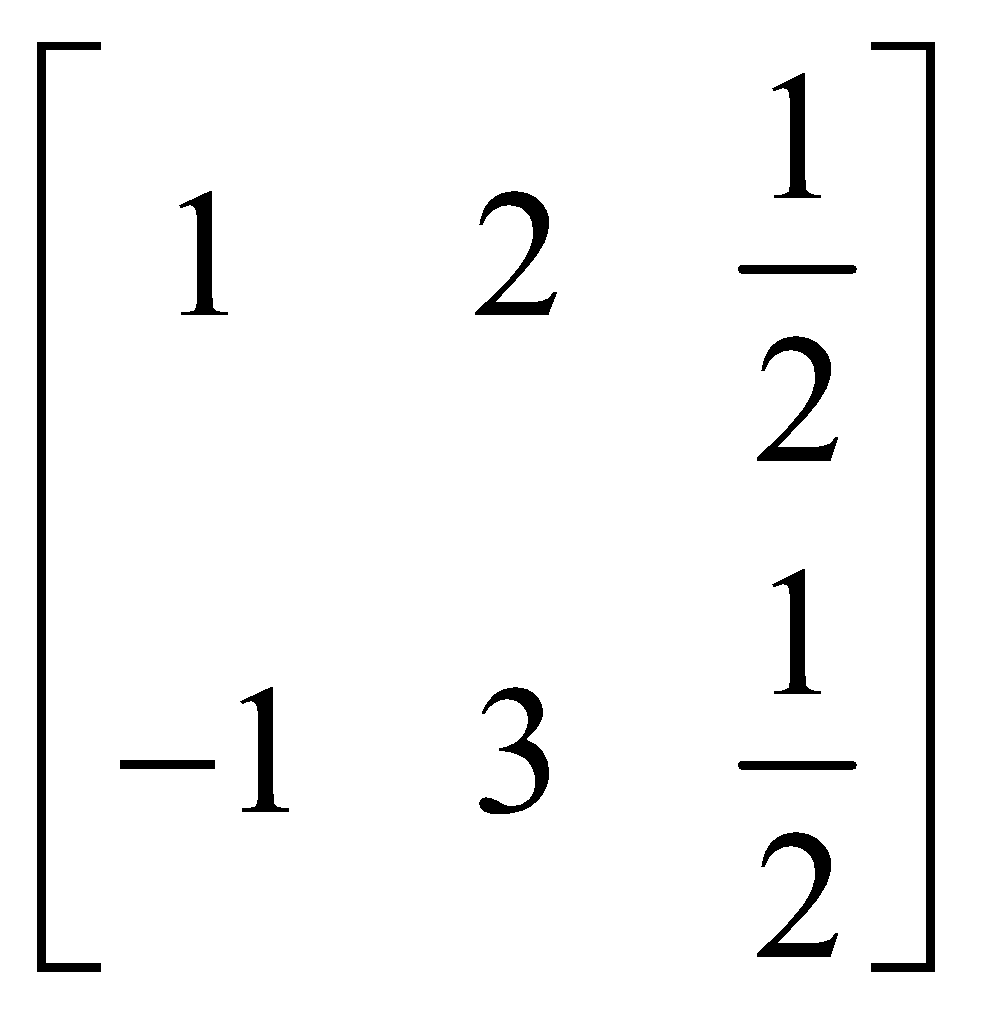
3. The addition to the elements of any row or column, the corresponding elements of any other row or column multiplied by any non zero number. Symbolically, the addition to the elements of ith row, the corresponding elements of jth row multiplied by k is denoted by Ri → Ri + kRj

The corresponding column operation is denoted by Ci → Ci + kCj. For example applying

R3 → R3 + 2R2 to C = 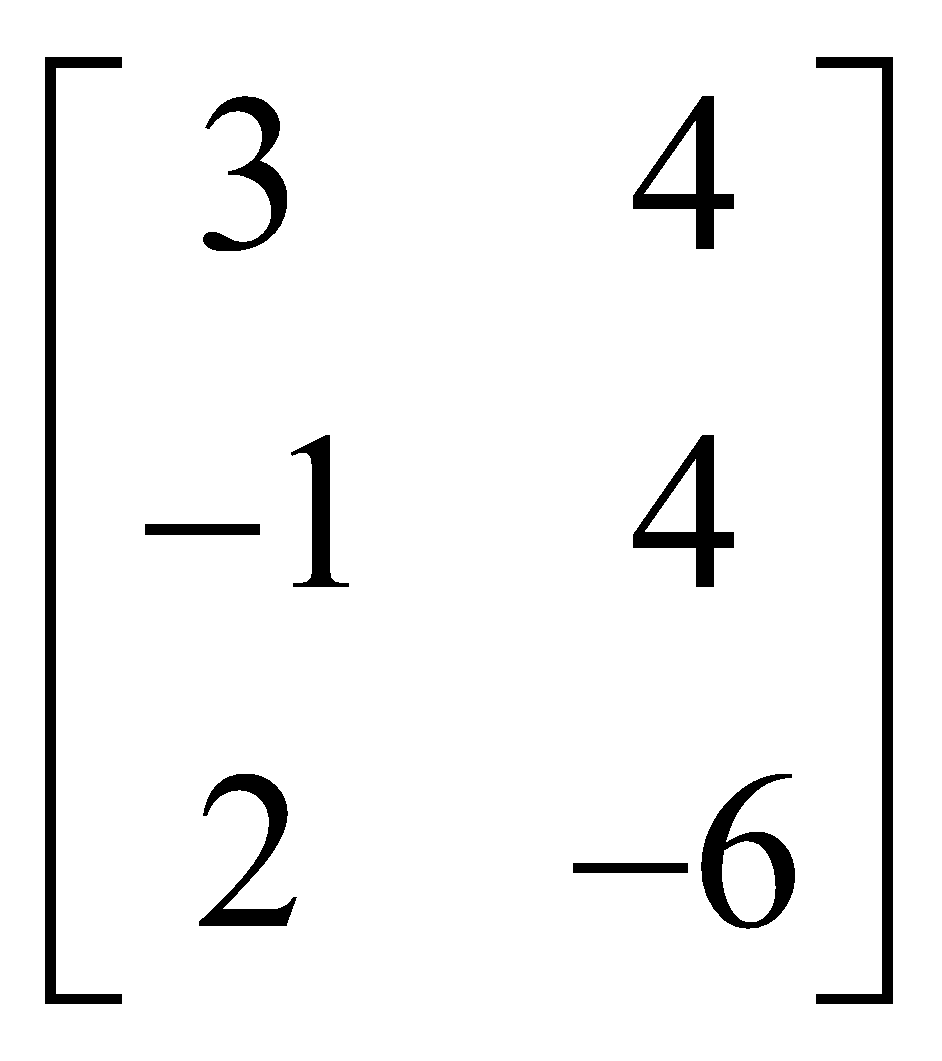, we get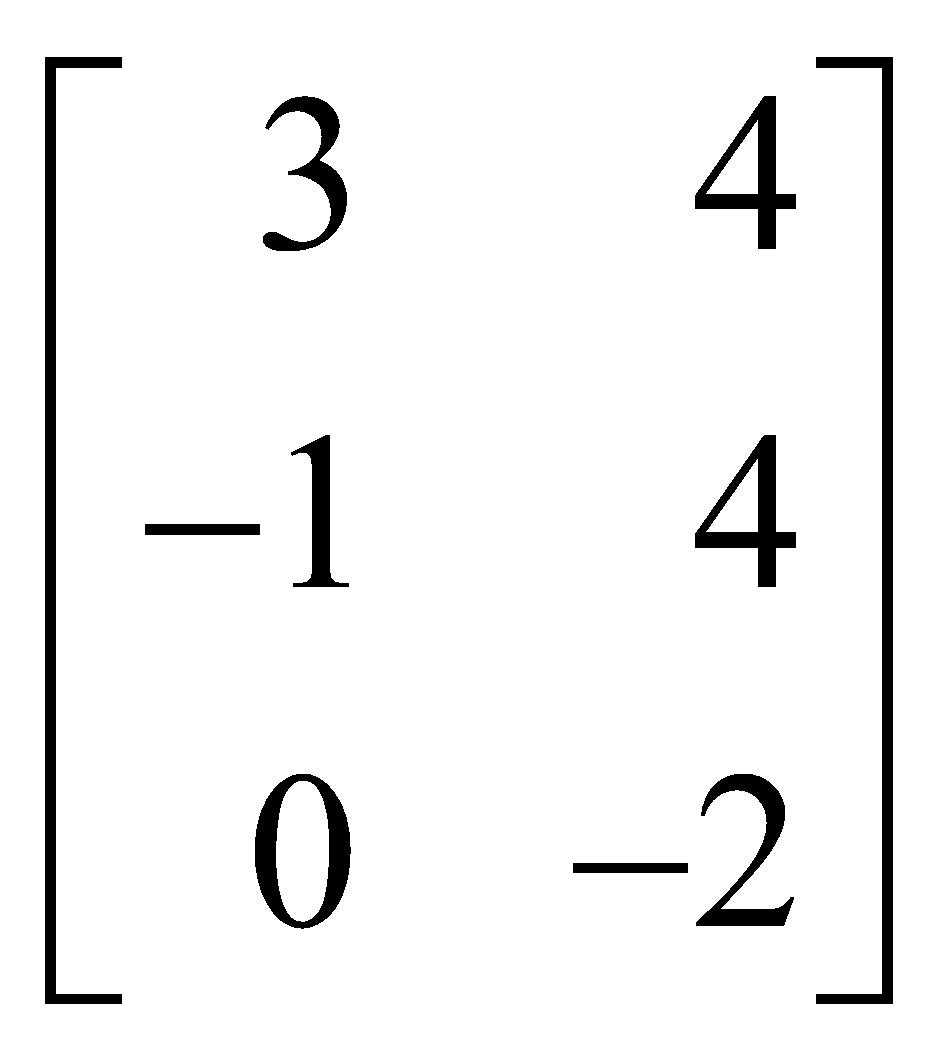  

INVERSE OF A MATRIX BY ELEMENTARY OPERATIONS

Let X, A and B be matrices of, the same order such that X = AB. In order to apply a sequence of elementary row operations on the matrix equation X = AB. We will apply these row operations simultaneously on X and on the first matrix A of the product AB on RHS.

Similarly, in order to apply a sequence of elementary column operations on the matrix equation X = AB, we will apply, these operations simultaneously on X and on the second matrix B of the product AB on RHS.

In view of the above discussion, we conclude that if A is a matrix such that A–1 exists, then to find A–1 using elementary row operations, write A = IA and apply a sequence of row operation on A = IA till we get, I = BA. The matrix B will be the inverse of A. Similarly, if we wish to find A–1 using column operations, then, write A = AI and apply a sequence of column operations on A = AI till we get, I = AB.

Remark : In case, after applying one or more elementary row (column) operations on A = IA (A = AI) if we obtain all zeros in one or more rows of the matrix A on L.H.S. then A–1 does not exist.

Example : By using elementary operations, find the inverse of the matrix A =

Solution : In order to use elementary row operations we may write A = IA.

or 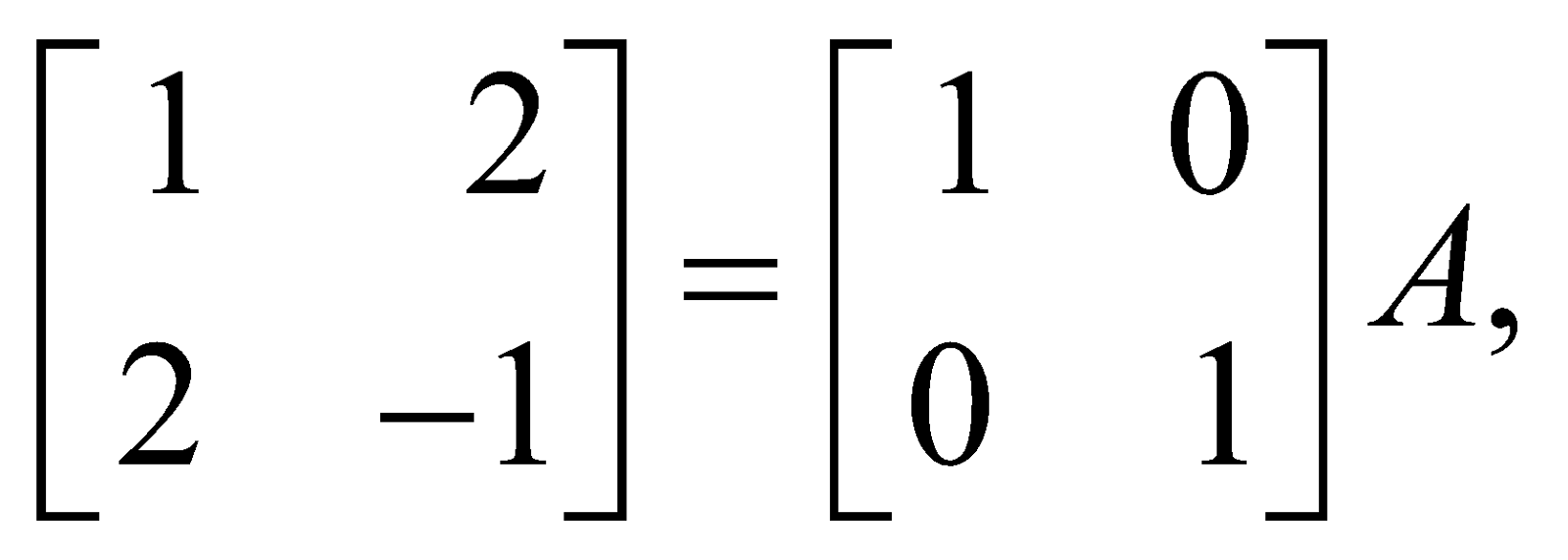 then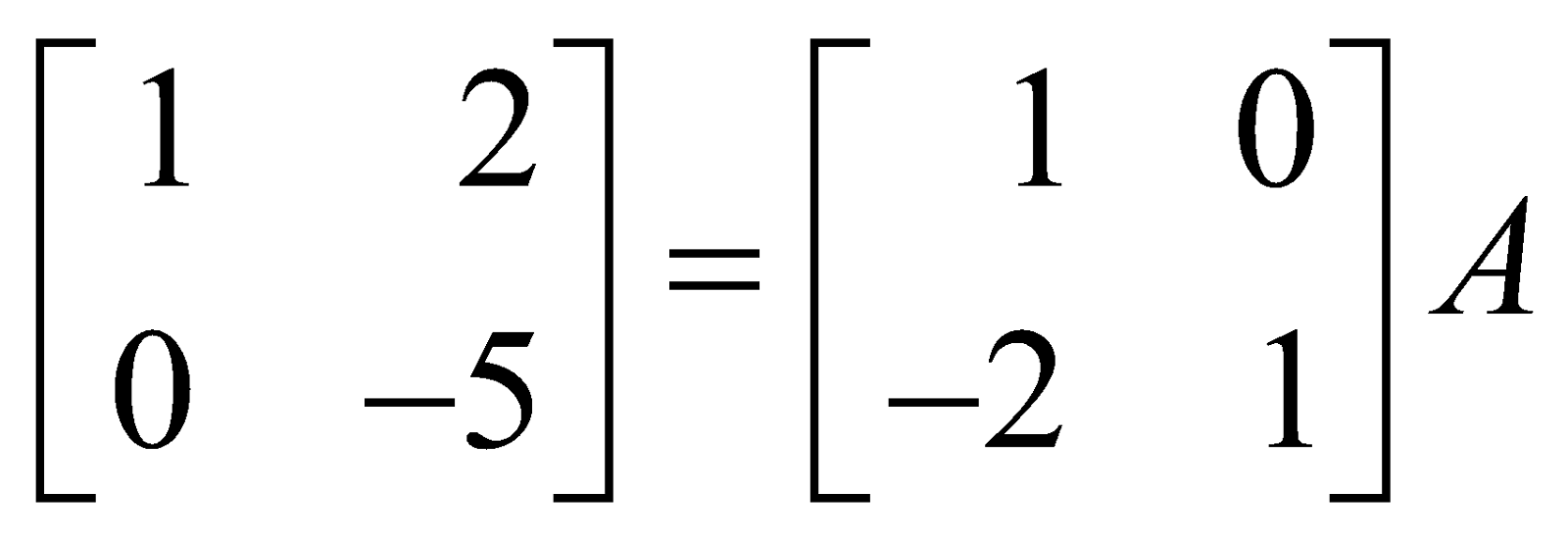

(applying R2 → R2 – 2R1)

or= 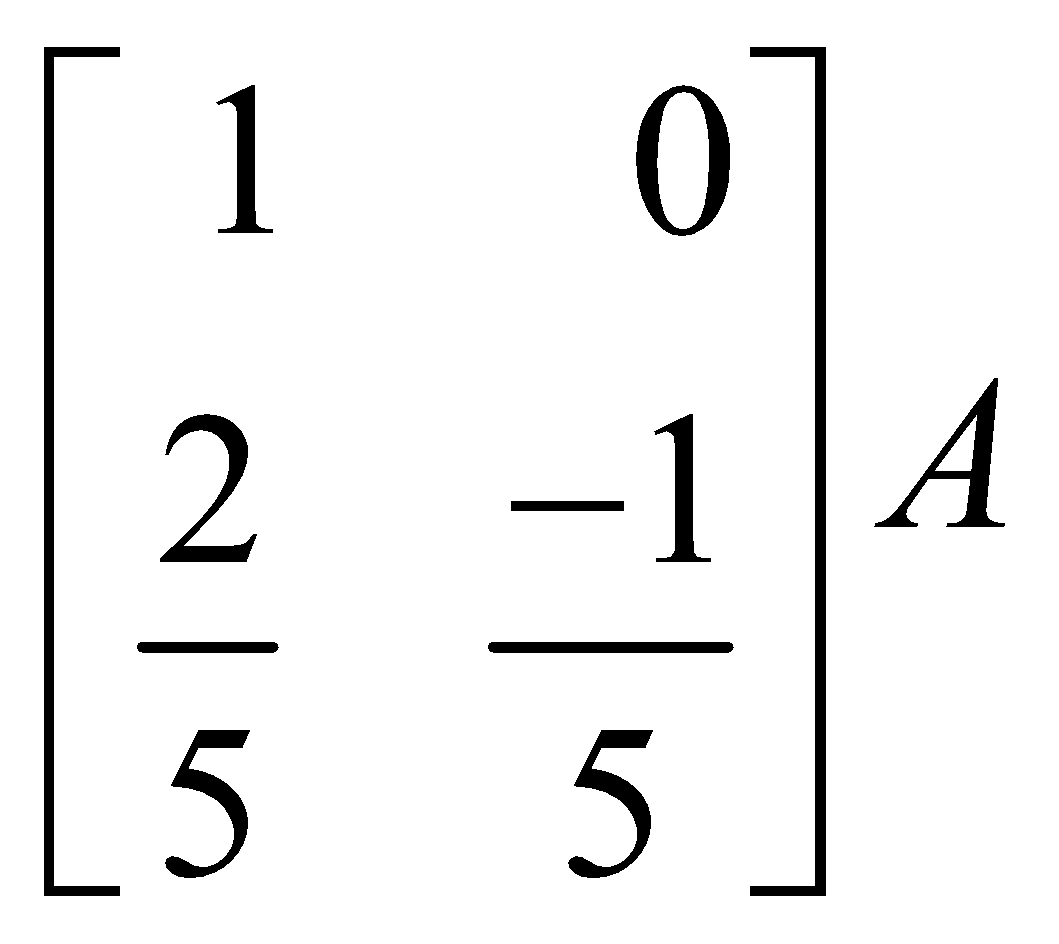(applying R2 → –R2)

or= (applying R1 → R1 – 2R2)

Thus A–1=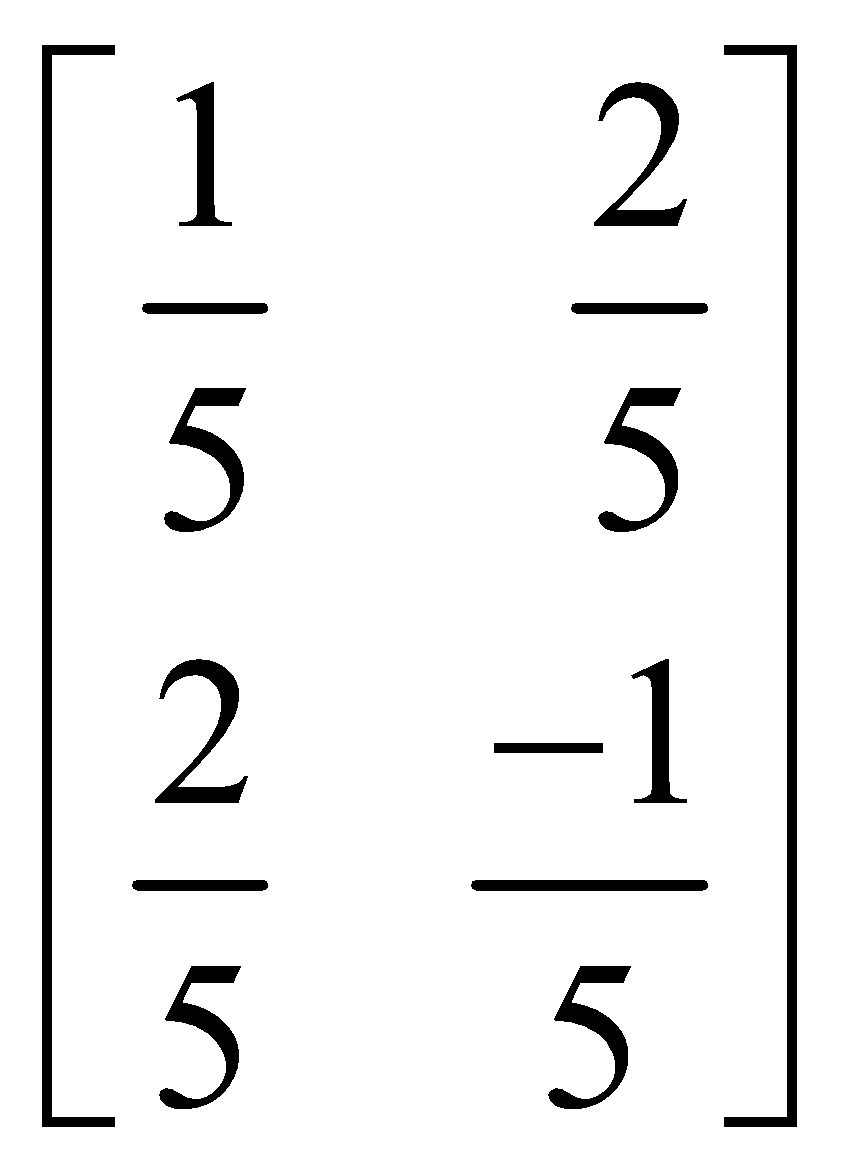

Alternatively, in order to use elementary column operations, we write A = AI, i.e.,

=

Applying C2 → C2 – 2C1 we get

=

Now applying we have

=

Finally, applying C1 → C1 – 2C2, we obtain

=

Hence A–1 =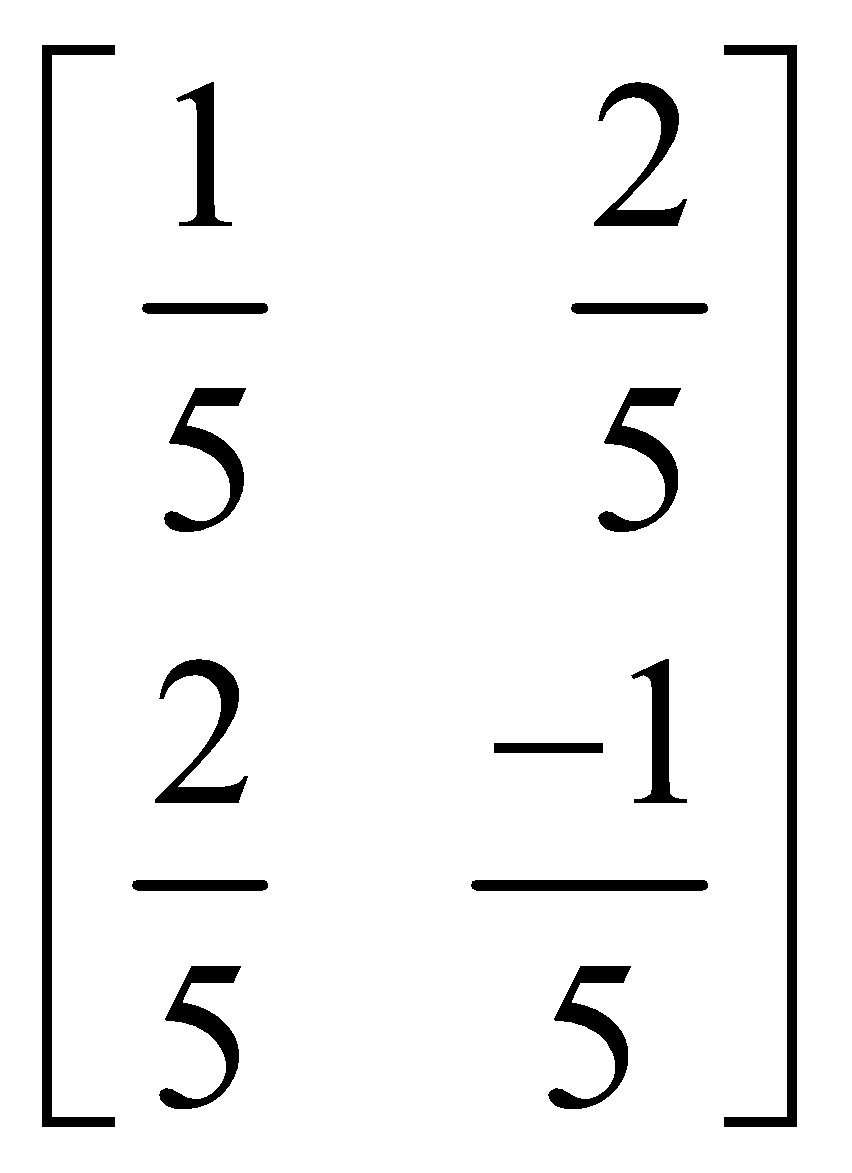

RANK OF A MATRIX

A positive integer r is said to be the rank of a non zero matrix A, if

• there exists atleast one minor in A of order r which is not zero,
• every minor in A of order greater than r is zero.

Rank is written as ρ (A) = r.

The rank of a zero matrix is defined to be zero.

For example , rank of is 2 because the minor  = 5 ≠ 0 and rank of  is 3 as the minor = 1 ≠ 0

For the square matrix A = we have |A| = 0,
since first two rows are proportional.

The minor = 0, but 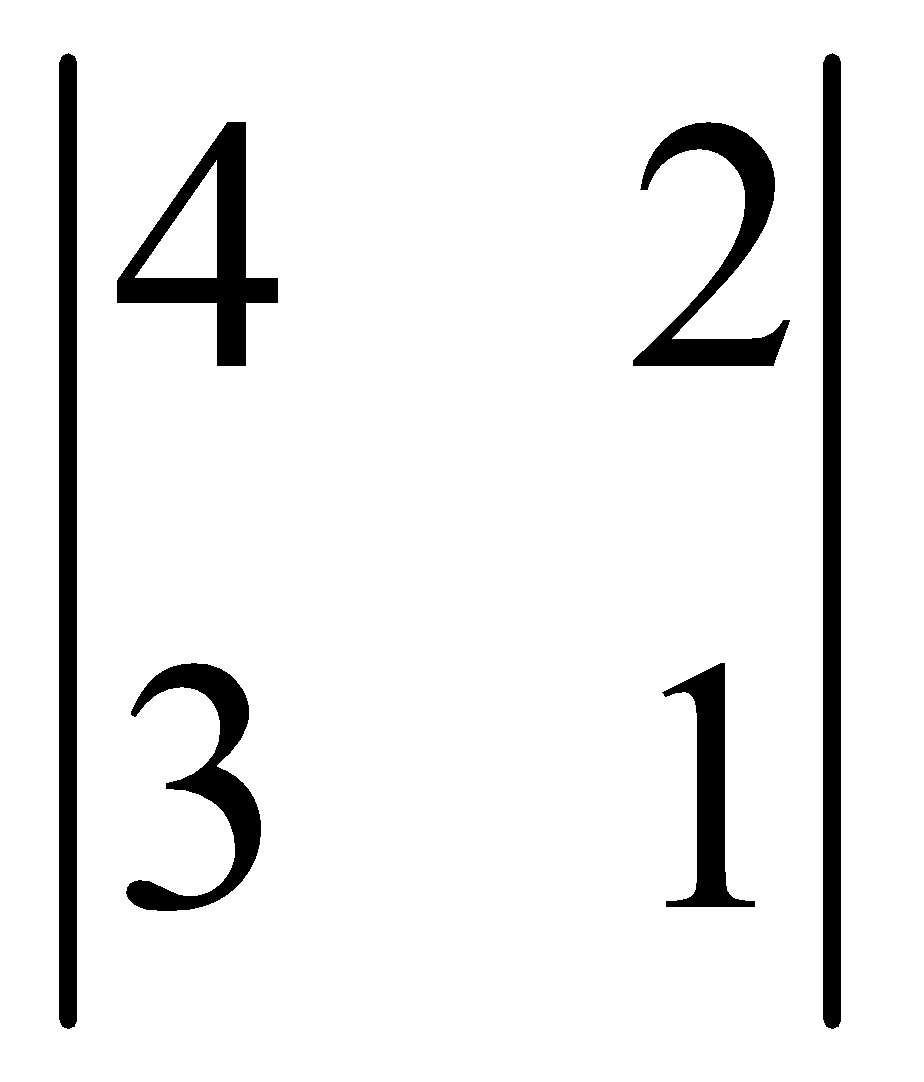= –2 ≠ 0.

Since atleast one minor of order 2 is not zero, therefore the rank of A is 2.

Let A =  be a 4 × 3 matrix.

The highest possible order of minors for the matrix = 3. Minors of  order 3 are the following :

Clearly the number of minors of the 3rd order =

Similarly, the number of minors of order 2 =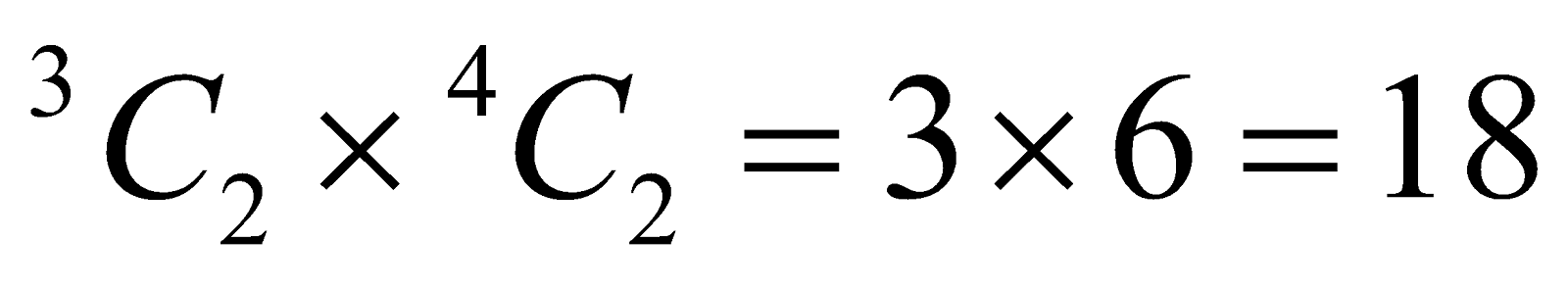

The rank of a matrix is the order of the highest order non-zero minor of the matrix.

For example, consider a matrix

One of the third order minors is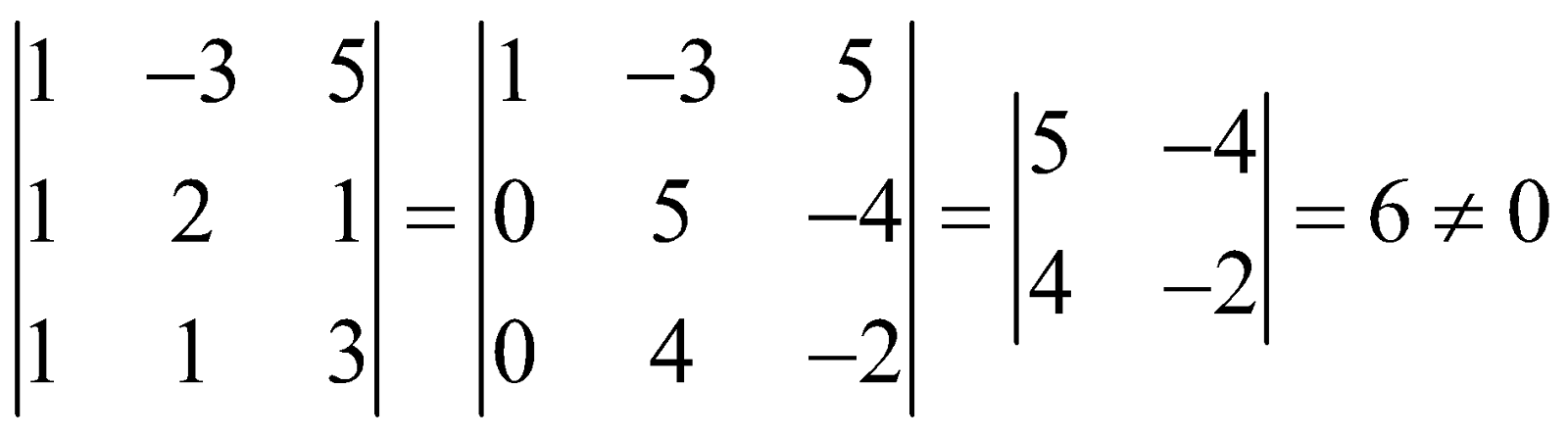

Order of the highest order non-zero minor of the matrix is 3. Therefore Rank of the given matrix = 3.

PROPERTIES

1. Rank of a matrix remains unaltered by elementary transformations.
2. No skew-symmetric matrix can be of rank 1.
3. Rank of matrix A = Rank of matrix AT.
4. AAT has the same rank as A.

SOLUTION OF SIMULTANEOUS LINEAR EQUATIONS USING MATRIX METHOD

SYSTEM OF EQUATIONS WITH TWO VARIABLES

Consider the two simultaneous equations in two variables x and y

These can be written in matrix form as

where A is a 2 × 2 matrix, and X and B are 2 × 1 column matrices.

Similarly the three simultaneous equations,

can be written in the matrix form as,

where A is a 3 × 3 matrix, and X and B are (3 × 1) column matrices.

If now A is non-singular, i.e., |A| ≠ 0, then we can left-multiply both members of this equation by A–1 to obtain

1. If |A|≠ 0 , the system is consistent and has a unique solution.
2. If |A| = 0, the system of equations has either no solution or an infinite number of solutions.
3. Find (adj A) B.
1. If (adj A) B ≠ 0, the system has no solution and is, therefore, inconsistent.
2. If (adj A) B = 0, the system is consistent and has infinitely many solutions. In this case we say that the equations are dependent equations.

SYSTEM OF HOMOGENEOUS LINEAR EQUATIONS

A linear equation is said to be homogeneous if the constant term is zero. The equations

;  ;

constitute a system of homogeneous linear equations.

If and, then the system of equations can be written as AX = 0.

Note that x = y = z = 0 always satisfy the equations.

Hence, the system is always consistent. The solution x = y = z = 0 is called the trivial solution.

Now let us find whether the system has non-trivial solutions. Suppose A is non-singular. Then exists and we get

Hence, if i.e. A is non-singular, the system has only trivial solution. Thus in order that the system AX = 0 has non-trivial solution, it is necessary that |A| = 0.

A system of n homogeneous linear equations in n unknown has non-trivial solutions if and only if the coefficient matrix is singular.

Criterion of consistency regarding solution of homogeneous linear equations given by AX = 0, where A is a square matrix, is as following

1. If | A | ≠ 0, then the system has only trivial solution.
2. If | A | = 0, the system has infinitely many solutions.

Note that if | A | = 0, then (adj A) B = 0 as B = 0.

Mathematics Study Notes

• Sets, Relations and Functions
• Trigonometric Ratios and Identities
• Trigonometric Equations and Inequations
• Properties of Triangles, Height and Distances
• Principle of Mathematical Induction, Permutation and Combination
• Complex Numbers
• Quadratic Equations
• Linear Inequalities
• Sequences and Series
• Binomial Theorem
• Infinite Series
• Points & Straight Lines
• Pair of Straight Lines
• Circles
• Parabola
• Ellipse and Hyperbola
• Mathematical Reasoning
• Statistics
• Probability Basic
• Functions
• Inverse Trigonometric Functions
• Matrices
• Determinants
• Limits, Continuity and Differentiability
• Differentiation and Application of Derivatives
• Indefinite Integration
• Definite Integration and Applications
• Differential Equations
• Vector Algebra
• Three Dimensional Geometry
• Probability Advanced

Study Notes for JEE Main/JEE Advanced/BITSAT