PAIR OF STRAIGHT LINES
GENERAL EQUATION OF A PAIR OF STRAIGHT LINES
Consider the equations of two straight lines
Their combined equation may be given by
On multiplying the left hand side of (1), we get an equation of the form  ......(2)
......(2)
where a = a1a2, 2h = a1b2 + a2b1, ...... etc.
The equation (2) is the most general equation of second degree, which will represent a pair of straight lines under certain conditions.
HOMOGENEOUS EQUATIONS OF SECOND DEGREE
An equation of the type
is a homogeneous equation of second degree. [Note that the sum of the powers of x and y in every term is the same and 2].
The homogeneous equation of the second degree always represents a pair of straight lines passing through the origin. We have
- If h2 > ab, the two lines are REAL AND DIFFERENT.
- If h2 = ab, the two lines are COINCIDENT.
- If h2 < ab, the two lines are IMAGINARY having origin as their real point of intersection.
If  represents the pair of lines y = m1x and y = m2x. Then
represents the pair of lines y = m1x and y = m2x. Then
Comparing the coefficients we get
ANGLE BETWEEN THE LINES GIVEN BY ax2 + 2hxy + by2 = 0
If the equation ax2 + 2hxy + by2 = 0 represents the straight lines y = m1x and y = m2x, then the acute angle θ, between the lines is given by
BISECTORS OF THE ANGLES BETWEEN THE LINES ax2 + 2hxy + by2 = 0
The equation of the pair of lines bisecting the angle between the lines given by is
is  or
or 
IMPORTANT RESULTS
- Two lines are coincident if tan θ = 0 i.e. if h2 – ab = 0
- Two lines are perpendicular of tan θ = ∞ i.e. if a + b = 0
∴ The equation of a pair of perpendicular straight lines can be given by ax2 + 2hxy – ay2 = 0
[Substituting b = –a]
or , where
, where 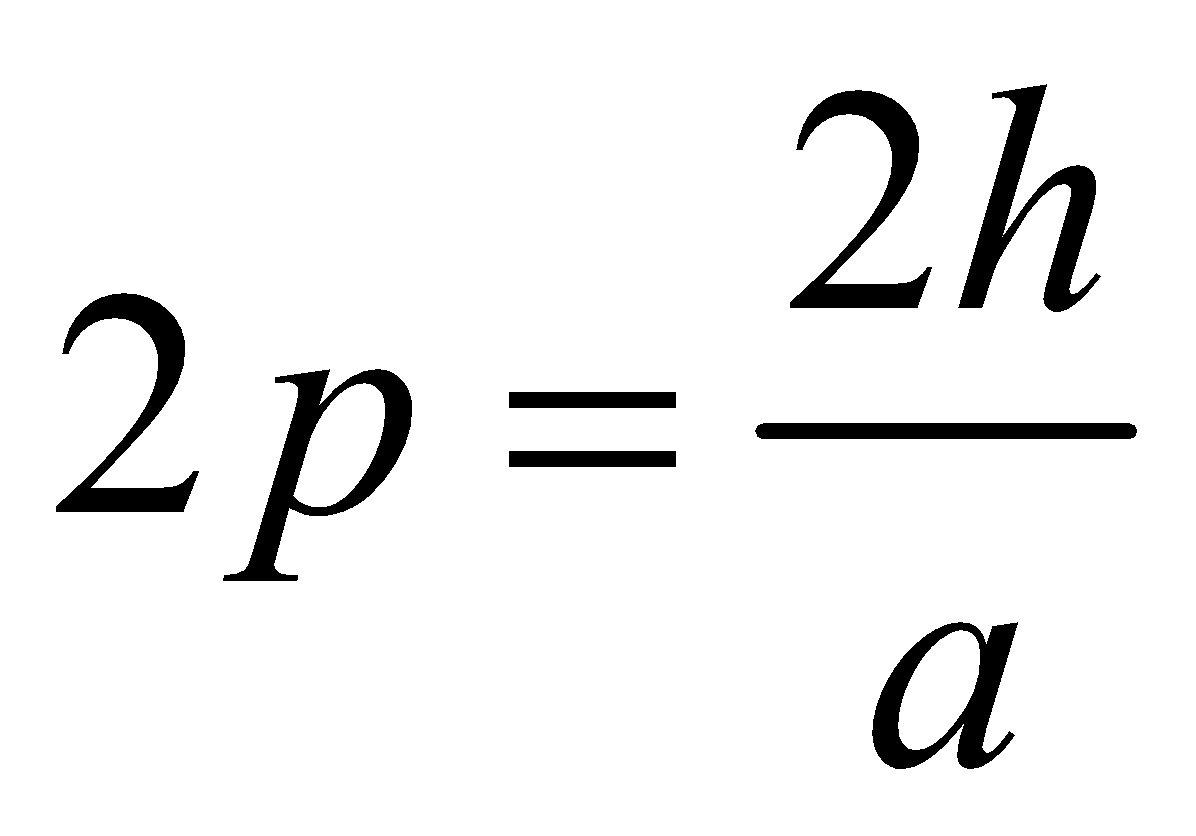
- If the lines given by the equation
are equally inclined to axes, then the coordinate axes are the bisectors, i.e. the equation of pair of bisector must be xy = 0. Therefore h = 0.
- If two pairs of straight lines are equally inclined to one another, then both must have the same pair of bisectors.
- Since coeff. of x2 + coeff. of y2 = 0. Therefore two bisectors are always perpendicular. (The original lines may or may not be perpendicular).
CONDITION THAT THE GENERAL EQUATION OF SECOND DEGREE MAY REPRESENT A PAIR OF STRAIGHT LINES
Let the general equation of the second degree be
ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 ...(1)
ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 ...(1)
It will represent a pair of straight lines if the left hand side is expressible as product of two linear factors, which is possible if abc + 2fgh – af2 – bg2 – ch2 = 0
or  ...(2)
...(2)
The expression (2) is also called the DISCRIMINANT of the equation (1).
IMPORTANT RESULTS
- Angle θ between the lines is given by
- The point of intersection of the pair of lines is
.
- The equation of the pair of angular bisectors is given by
, where (x1, y1) is the point of intersection of two lines. [It is obtained by replacing x by x – x1 and y by y – y1 in the equation
AN ALTERNATE METHOD FOR FINDING POINT OF INTERSECTION
Let ax2 + 2hxy + by2 + 2gx + 2fy + c or  represents a pair of straight lines.
represents a pair of straight lines.
Find , i.e. differentiate
, i.e. differentiate  with respect to x treating y as a constant.
with respect to x treating y as a constant.
Then
Similarly find  (φ is differentiated with respect to y treating x as a constant)
(φ is differentiated with respect to y treating x as a constant)
Solve the equations  to get the required point of intersection.
to get the required point of intersection.
Thus solving the equations ax + hy + g = 0 and hx + by + f = 0, we get
SEPARATION OF THE EQUATIONS OF LINES
Let the equation ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 represents the straight lines y = m1x + c1 and y = m2x + c2.
Then, ax2 + 2hxy + by2 + 2gx + 2fy + c
=b (y – m1x – c1) (y – m2x – c2)
Comparing the coefficients, we get
USEFUL RESULTS
- The two lines are parallel if h2 – ab = 0
- The two lines are perpendicular if a + b = 0
- The two lines are coincident if h2 – ab = g2 – ac = f2 – bc = 0
- Distance between the parallel lines : If the two lines represented by eqn. (1) are parallel, then the distance between the two parallel lines is given by
- The two pairs of straight lines ax2 + by2 + 2hxy + 2gx + 2fy + c = 0 and ax2 + by2 + 2hxy = 0 form a
- square if (a – b) fg + h (f2 – g2) = 0, a + b = 0
- rectangle if (a – b) fg + h (f2 – g2) ≠ 0, a + b = 0
- rhombus if (a – b) fg + h (f2 – g2) = 0, a + b ≠ 0
- parallelogram if (a – b) fg + h (f2 – g2) ≠ 0, a + b ≠ 0
EQUATION OF THE PAIR OF STRAIGHT LINES JOINING THE ORIGIN TO THE POINTS OF INTERSECTION OF A CURVE AND A STRAIGHT LINE
Let the equation of the given curve be
and the equation of the straight line be
L : lx + my + n = 0.
To find the equation of the pair of straight lines joining the points of intersection A and B of the curve S = 0 and the line L = 0 with the origin O, we homogenise the equation S = 0, with the help of L = 0. For this, we write
⇒ ax2 + 2hxy + by2 + 2 (gx + fy) 
which is homogeneous equation of the second degree and gives the required pair of straight lines.
PROCEDURE
- Divide the equation of the line L = 0 by the negative of constant term and write it as
- Multiply the single degree terms by 1 and the absolute terms by 12 in the equation of the curve and put the value of 1 as obtained in above step 1.
TRANSLATION OF AXES
A change of origin without changing the direction of coordinate axes is called a translation of axes.
Let xoy represent the initial system. The origin is shifted to a new point O maintaining the axes parallel to original position then the new system is XOY.
Let the coordinates of O with respect to initial system are (h, k).
Suppose P is a point in the plane whose coordinates are (x, y) initially and (X, Y) in the translated system.
Then x = X + h and y = Y + k
Therefore the equation of any curve f(x, y) = 0 will become f(X + h, Y + k), where reference is taken on the translated axes.
ROTATION OF AXES
Let xoy represent the initial system. Now the axes are rotated by θ angle anticlockwise keeping the origin unchanged, then the new system is XOY.
Let P is a point in the plane whose coordinates are (x, y) initially and (X, Y) in the new system.
Then, x = Xcos θ – Y sin θ; y = X sin θ + Y cos θ
and X = x cos θ + y sin θ; Y = –x sin θ + y cos θ
The above result can be remembered by the following matrix equation.







