QUADRATIC EQUATIONS
QUADRATIC EQUATION
A quadratic equation can be expressed as
ax2 + bx + c = 0, a ≠ 0 ...(1)
Where a, b and c are complex numbers
The expression f(x) = ax2 + bx + c, is called a quadratic trinomial expression.
ROOTS OF A QUADRATIC EQUATION
- The values of x, which satisfy the above written equation (1) are called the roots of the quadratic equation.
A quadratic equation has two and only two roots.
- The roots of the quadratic equation (1) can be evaluated using the following formula.
The above formula provides both the roots of the quadratic equation, which are generally denoted by α and β,
say  and
and 
QUADRATIC EQUATIONS WITH REAL COEFFICIENTS
Consider the quadratic equation
Where, a, b, and c are real number
The formula is applicable to solve any kind of quadratic equation whether it has real coefficients or complex coefficients, However, onwards we will strictly discuss only those equations, which have real coefficients unless stated otherwise.
is applicable to solve any kind of quadratic equation whether it has real coefficients or complex coefficients, However, onwards we will strictly discuss only those equations, which have real coefficients unless stated otherwise.
The expression inside the square root is called the DISCRIMINANT of the quadratic equation and denoted by D. Thus, Discriminant (D) = b2 – 4ac.
NATURE OF ROOTS
The nature of roots of the equation depends upon the nature of its discriminant D.
- If D < 0, then the roots are non-real complex, Such roots are always conjugate to one another. That is, if one root is p + iq then other is p – iq, q ≠ 0.
- If D = 0, then the roots are real and equal. Each root of the equation becomes
. Equal roots are referred as repeated roots or double roots also.
- If D > 0 then the roots are real and unequal.
- In particular, if a, b, c are rational number, D > 0 and D is a perfect square, then the roots of the equation are rational number and unequal.
- If a, b, c, are rational number, D > 0 but D is not a perfect square of a rational number, then the roots of the equation are irrational (surd). Surd roots are always conjugate to one another, that is if one root is
. then the other is
, q > 0.
- If a = 1, b and c are integers, D > 0 and perfect square, then the roots of the equation are integers.
IMPORTANT RESULT
- The condition that the roots of a quadratic equation are real is i.e.
- The quadratic trinomial will be a perfect square if D = 0 i.e.
- If
is a repeated root of the quadratic equation
then
is a root of equation as well.
- If a, b, c are non real and the quadratic equation has non-real roots, then the roots need not be conjugate.
- If a, b, c are irrational and the quadratic equation has irrational roots, then the roots are not necessarily conjugate.
- If a + b + c = 0 then one root is always unity and the other root is
, Hence the roots are rational provided a, b, c, are rational.
SIGN OF ROOTS
Let α, β are real roots of the quadratic equation that is D =  . Then
. Then
- Both the roots are positive if a and c have the same sign and the sign of b is opposite.
- Both the roots are negative if a, b and c all have the same sign.
- The Roots have opposite sign if sign of a and c are opposite.
- The Roots are equal in magnitude and opposite in sign if b = 0 [ that is its roots are α and –α]
- The roots are reciprocal if a = c. [i.e., the roots are α and
]
- If c = 0. then one root is zero
- If b = c = 0, then both the roots are zero.
- If a = 0, then one root is infinite
- If a = b = 0, then both the roots are infinite
- If a = b = c = 0, then the equation becomes an identity
IMPORTANT RESULTS
- If a and b have the same sign then the real part of roots is negative (if no restriction is given on D)
- If a and b have opposite sign then the real part of roots is positive (if no restriction is given on D)
- If a and c have opposite sign then the roots of the equation are always real.
- To find a quadratic equation which has roots –α, –β, replace x by –x.
- To find a quadratic equation which has roots
and
replace x by
.
- If we replace x by x2, the resulting equation has four degrees and its roots are α, –α, β,–β,
- If a quadratic equation has more than two roots then it must be an identity.
SYMMETRIC FUNCTIONS OF ROOTS
An expression in α, β is called a symmetric function of α, β if the function is not affected by interchanging α and β. If α, β are the roots of the quadratic equation  then,
then,
Sum of roots 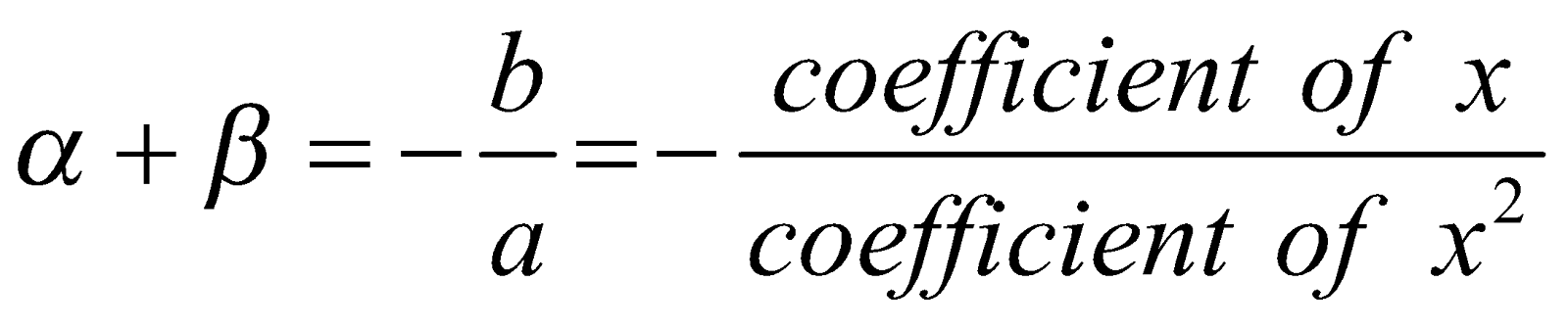
Product of roots 
Note :
- Above relations hold for any quadratic equation whether the coefficients are real or nonreal complex.
- With the help of above relations many other symmetric functions of α and β can be expressed in terms of the coefficients a, b and c.
- Recurrence Relation
- Some symmetric functions of roots are
The relations (ii) (iii), (v) and (vii) are not symmetric functions.
FORMATION OF QUADRATIC EQUATION WITH GIVEN ROOTS
- An equation whose roots are α and β can be written as (x – α) (x – β) = 0 or x2 – (α + β) x + αβ = 0 or x2 – (sum of the roots) x + product of the roots = 0.
- Further if α and β are the roots of a quadratic equation ax2 + bx + c = 0, then
ax2 + bx + c = a(x – α) (x – β) is an identity.
A number of relations between the roots can be derived using this identity by substituting suitable values of x real or imaginary.
CONDITION OF A COMMON ROOT BETWEEN TWO QUADRATIC EQUATIONS
Consider two quadratic equations
and  ...(ii)
...(ii)
Let α is a common root of the two equations
Then  and
and 
On solving we get 
or 
Which gives the common root as well as the condition for common root.
CONDITION THAT TWO QUADRATIC EQUATIONS HAVE BOTH THE ROOTS COMMON
Suppose that the equations 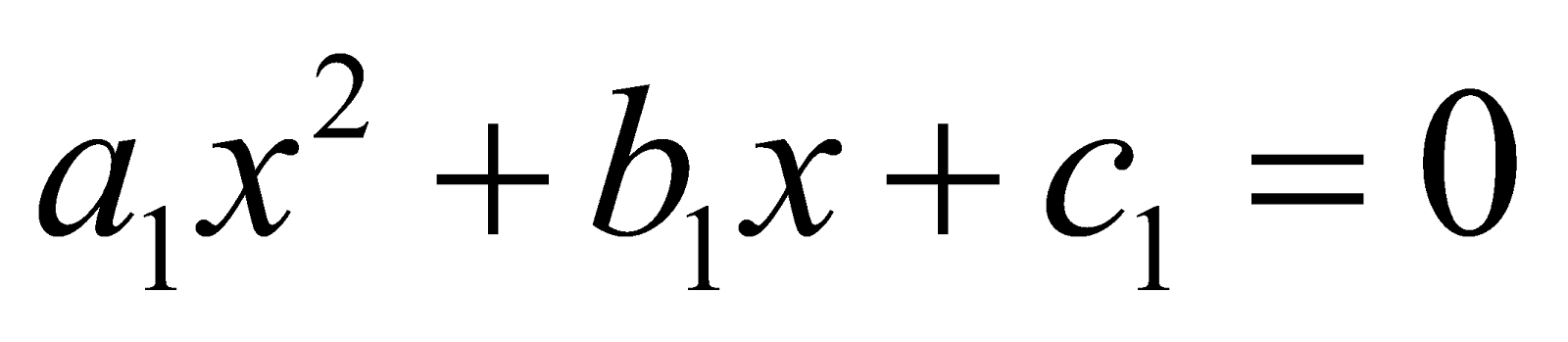 and
and  have both the roots common.
have both the roots common.
then 
If the coefficients of two quadratic equations are rational (real) and they have one irrational (imaginary) root common then they must have both the roots common as such roots occur in conjugate pair.
IMPORTANT RESULTS
- To find the common root of two equations, make the coefficient of second degree terms in two equations equal and subtract. The value of x so obtained is the required common root.
- If two quadratic equations with real coefficients have an imaginary root common, then both roots will be common and the two equations will be identical. The required condition is :
- If two quadratic equations with rational coefficient have an irrational root common, then both roots will be common and the two equations will be identical. The required condition is :
- If α is repeated common root of two quadratic equations f(x) = 0 and
, then α is also a common root of the equation f'(x) = 0 and
.
- Previous four articles are applicable for any kind of quadratic equation whether coefficients are real or nonreal complex.
EQUATIONS REDUCIBLE TO QUADRATIC FORM
There are certain equations which are not quadratic equations but can be converted to quadratic equations
FORM 1 : Equations of the form 
Procedure :
(i) Put f(x) = y and resulting equation becomes
ay2 + by + c = 0, a quadratic equation
(ii) Solve the quadratic equation by usual method to get two values of y.
(iii) Resubstitute y = f(x) and find x.
FORM 2 : Equations of the form 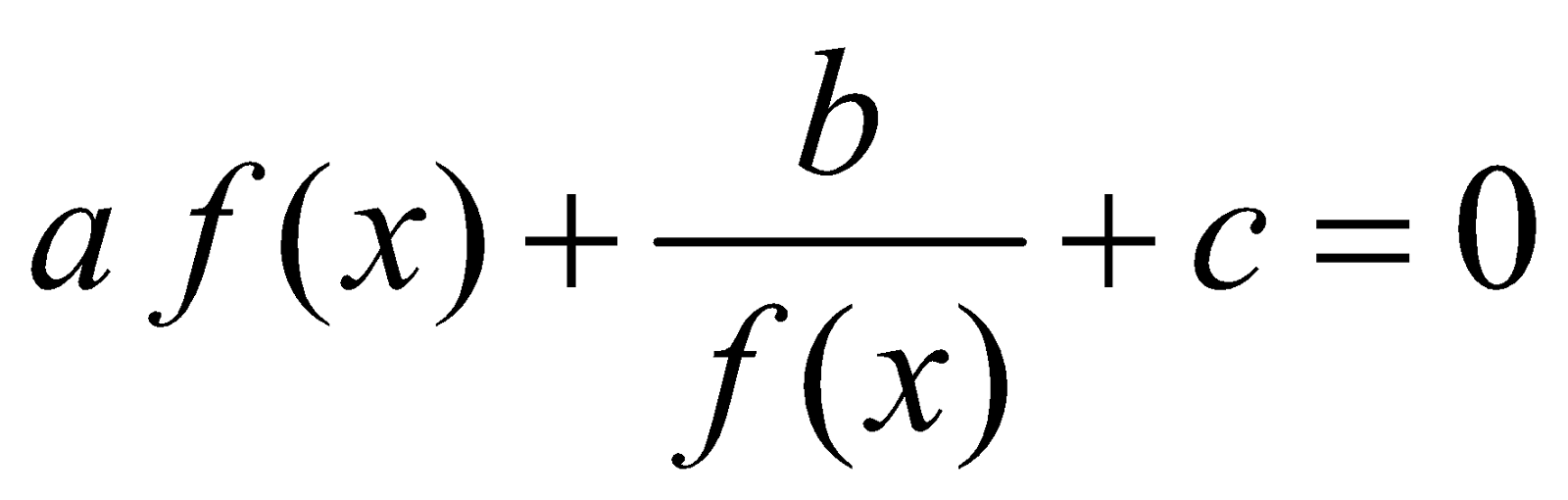
Procedure :
Put f(x) = y and resulting equation becomes , a quadratic equation. where y = f(x) ≠ 0
, a quadratic equation. where y = f(x) ≠ 0
Put f(x) = y and resulting equation becomes
FORM 3 : Equations of the form apx + bqx + c = 0, where pq = 1
Procedure : Put px = y then  and the resulting equation becomes
and the resulting equation becomes
FORM 4 : Equations of the form apx + bqx + crx = 0, where p, q, r, form a G.P. i.e. 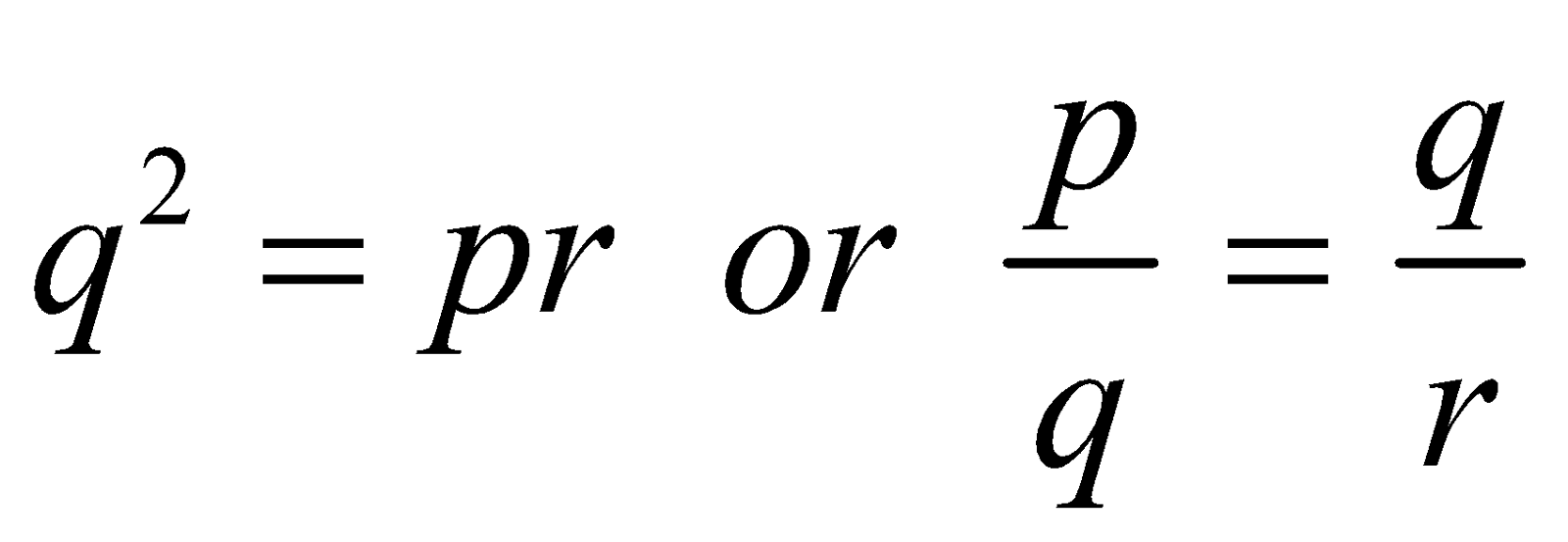
Procedure :
(i) Divide the equation by qx, we get 
(ii) Put 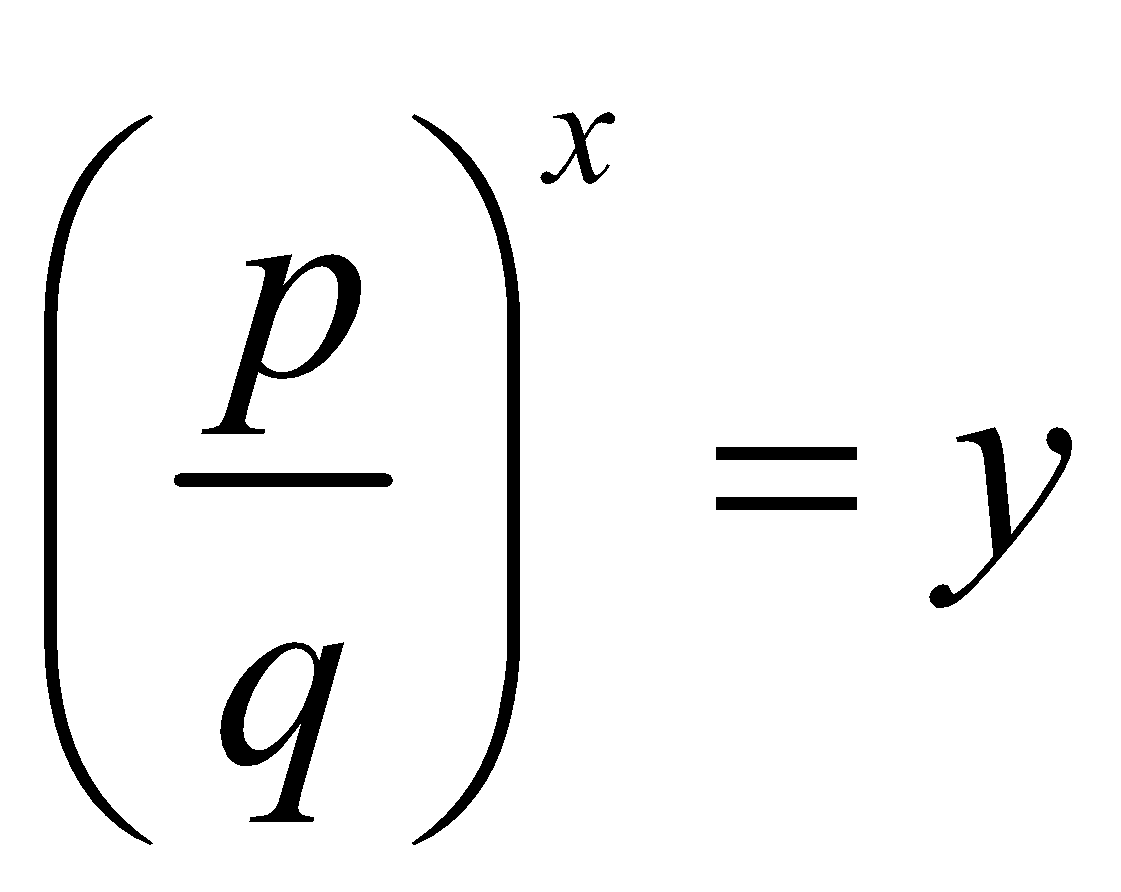 then
then  and the resulting equation is
and the resulting equation is , a quadratic equation.
, a quadratic equation.
FORM 5 : Equation of the form (x + a)(x + b)(x + c)(x + d) = k, where a +b = c + d.
Procedure :
Expand the equation in pairs as following :
for a + b = c + d
Let x2 + (a + b)x = y and the equation reduces to (y + ab)(y + cd) = k, a quadratic equation
FORM 6 : Equation of the form (x + a)(x + b)(x + c)(x+d) = kx2, where ab = cd
Procedure :
Expand the equation in pairs as following
Divide both the sides by x2, we get
Let  and the equation reduces to (y +a + b)(y + c + d) = k, a quadratic equation
and the equation reduces to (y +a + b)(y + c + d) = k, a quadratic equation
FORM 7 : Reciprocal Equations ax4 ± bx3 + cx2 ± bx + a = 0 [Reciprocal equations have equal coefficients in terms equidistant from beginning and end]
Procedure : Divide both the side by x2 ,we get
Put  such that
such that  or
or 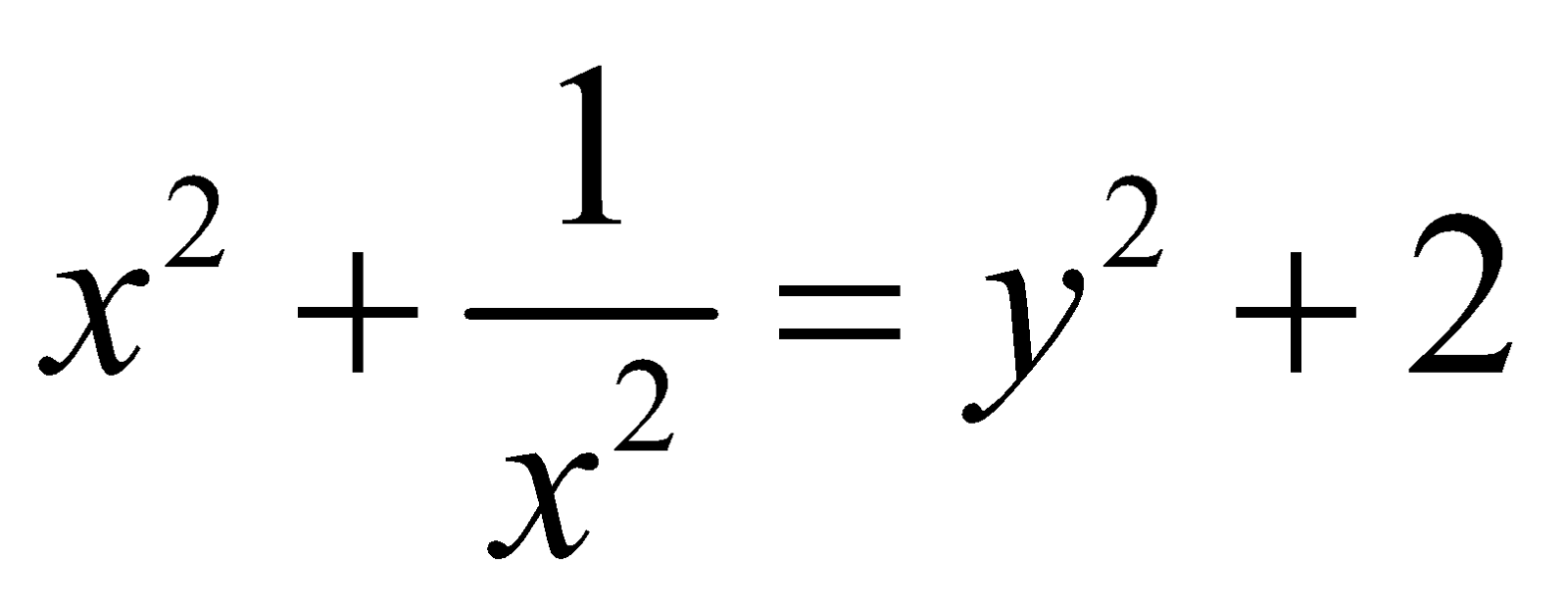 respectively.
respectively.
On substitution the original equation reduces to quadratic equation.
FORM 8 : Equation of the form  where
where 
Procedure : Put 
and 
We get 
On expanding it transforms to a quadratic in y2.
Note : In all of the above forms, after substitution the domain of equation often changes, so care must be taken to eliminate erroneous roots or inclusion of missing roots if any.
ANALYSIS OF QUADRATIC TRINOMIAL
Let 

 . We may write
. We may write
where 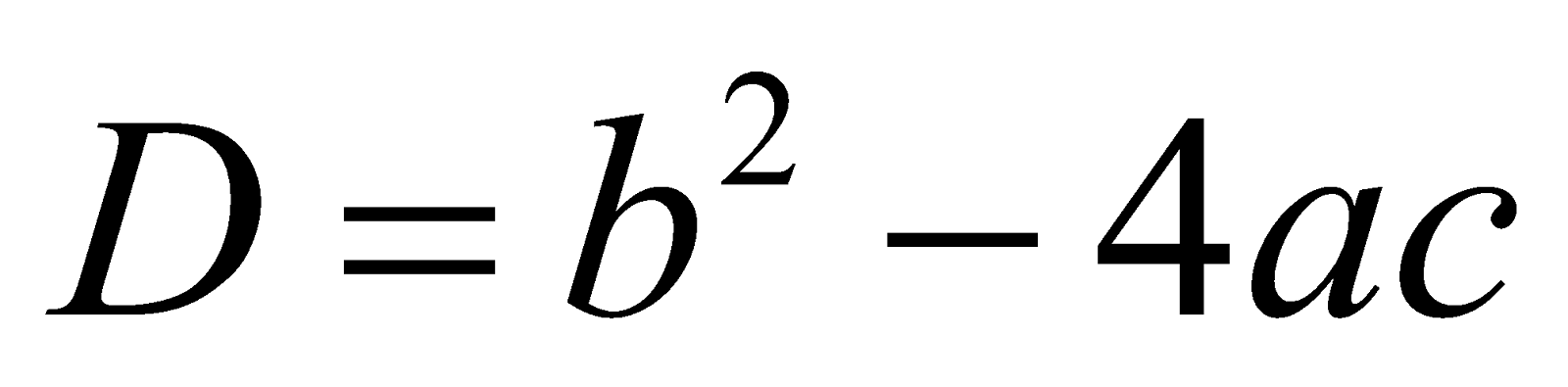 is the discriminant of the quadratic.
is the discriminant of the quadratic.
The equation represents a parabola, whose axis is parallel to the y-axis and vertex lies at 
CASE 1 : If a > 0, the parabola  will be concave upward. The position of vertex depends on sign of discriminant D.
will be concave upward. The position of vertex depends on sign of discriminant D.
- Let D < 0, then vertex lies above the x -axis.
- Let D = 0 then the vertex lies upon the x-axis.
- Let D > 0, then the vertex lies below the x-axis, hence, the parabola cuts x-axis at two points
and
, where
and
represent roots of
Then,
f(x) > 0 ifand
if
- In each of the above three situations, the minimum value of
is
, or the range of value of is
CASE 2 : If a < 0, the parabola 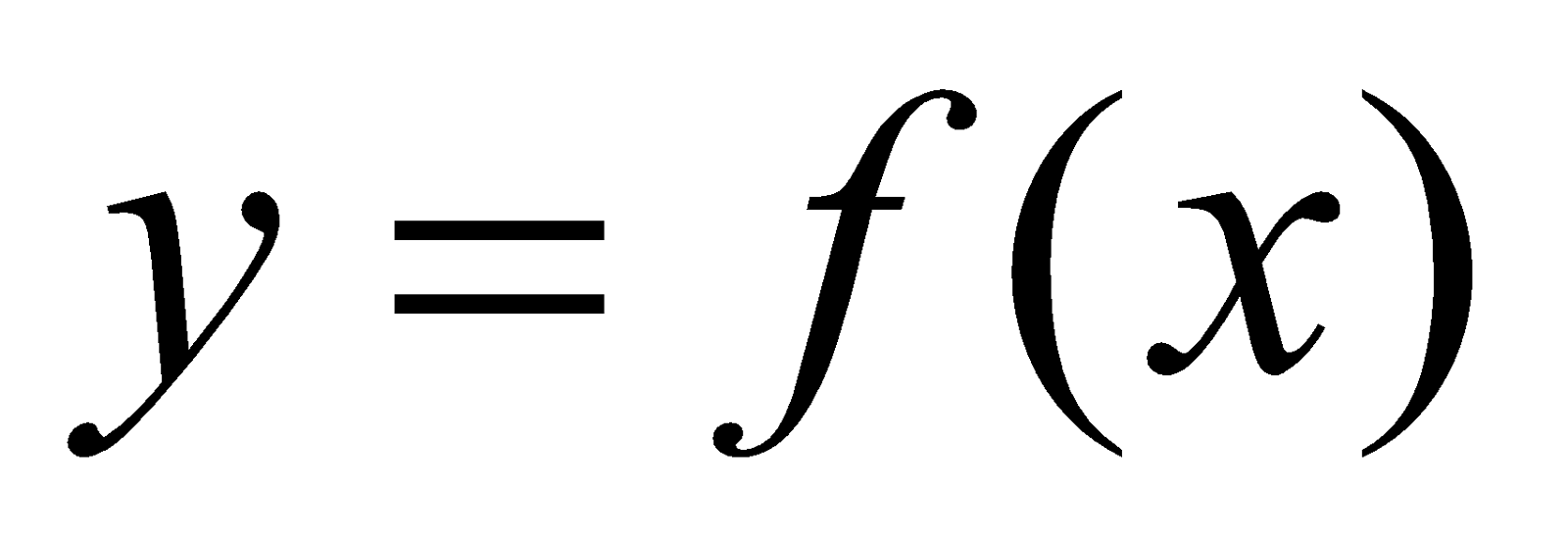 will be convex upward. The position of vertex again depends on sign of discriminant D
will be convex upward. The position of vertex again depends on sign of discriminant D
- Let D< 0, then vertex lies below the x-axis.
- Let D = 0, then vertex lies upon the x-axis
- Let D > 0, then vertex lies above the x-axis, hence, the parabola cuts x-axis in two points and , where and represent the roots of then,
f(x) > 0, if  and
and 
- In each of the above three situations, the maximum value of
is
, or the range of values of f(x) is
.
The above analysis will be applied for the problems of the following types :
PROBLEMS RELATED TO SIGN OF QUADRATICS
From the above analysis, we conclude that
- If
then
For example :
The quadratic
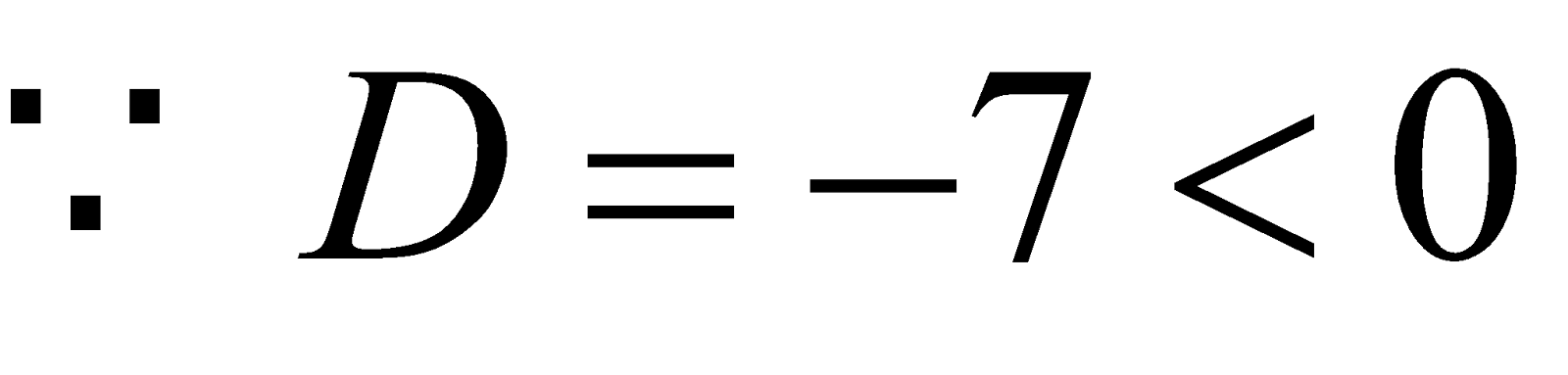
The quadratic 
 and a = –1
and a = –1
- If D = 0, then
For example :
Actually  and
and  , if x =1
, if x =1
- If D > 0, then
, if
and
if
, where
and
are the roots of
;
For example :
if x < –1 or x > 2 i.e
and
if
i.e
Here D = 9 > 0 and a = 1 and roots of x2 – x – 2 = 0 are –1 and 2
if
or
and
if
or
or 
Here D = 25 > 0 and a = –6 and roots of are
are  and
and 
Here D = 25 > 0 and a = –6 and roots of
- The quadratic ax2 + bx + c is positive definite (i.e., always positive) if D < 0 and a > 0
The quadratic ax2 + (2a – 1) x + a + 4 is always positive if  and
and
The common values in  and
and  are
are 

- The quadratic ax2 + bx + c is negative definite (i.e always negative) if D < 0 and a < 0.
For example :
- The quadratic
is always negative if a < 0 and
The common values of a < 0 and  do not exist.
do not exist.

- The quadratic is
always negative if
and 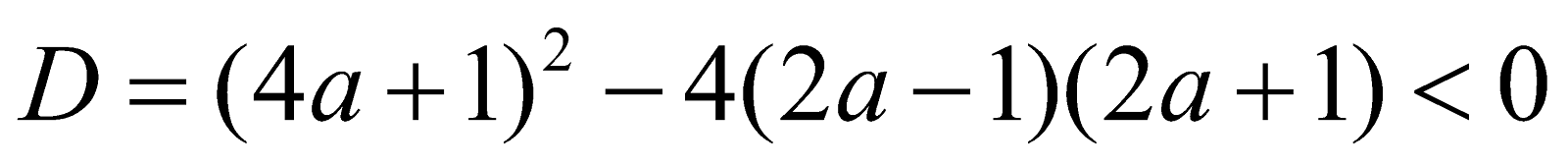
The common values of 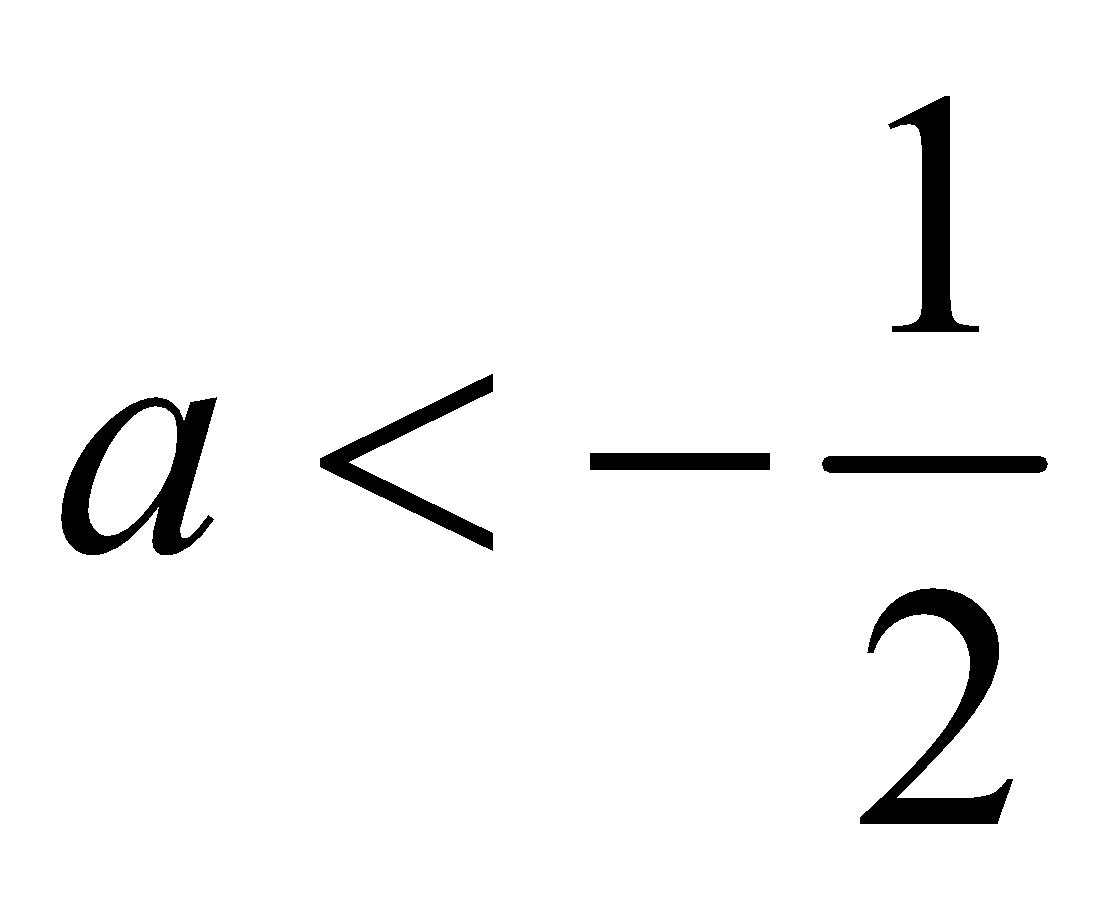 and
and 
- In case, the conditions are required for the quadratic to be always non-negative or non-positive in above (d) and (e), we replace the condition D < 0 by
in each case.
PROBLEMS RELATED TO SOLUTIONS OF QUADRATIC INEQUATIONS
From the analysis of quadratic trinomial ax2 + bx + c we can derive following procedure for the solutions of inequations of the type ax2 + bx + c > 0; ax2 + bx + c < 0;  ;
;  .
.
- Convert sign of ‘a’ positive by multiplying the inequation by –1. For example,
is converted to
- Evaluate discriminant
If D < 0, then

i.e  for any x.
for any x.
If D = 0, then 
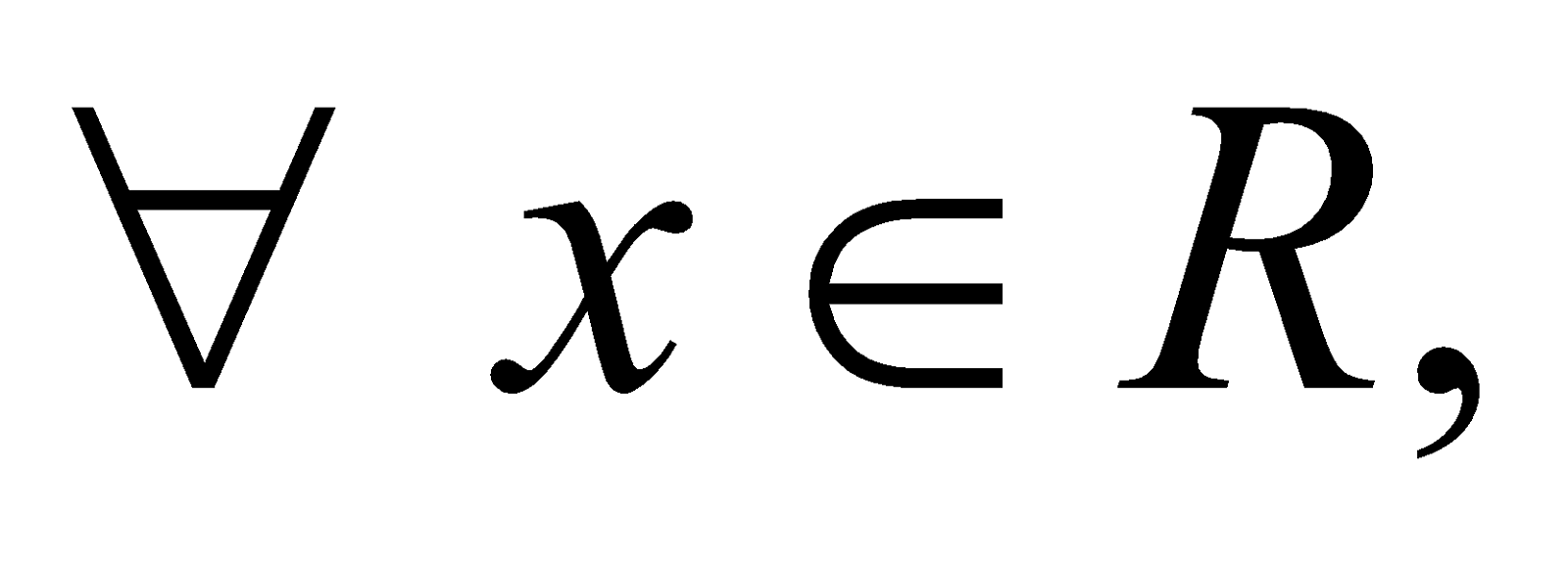
i.e  for any x
for any x
If D > 0, then find the roots of 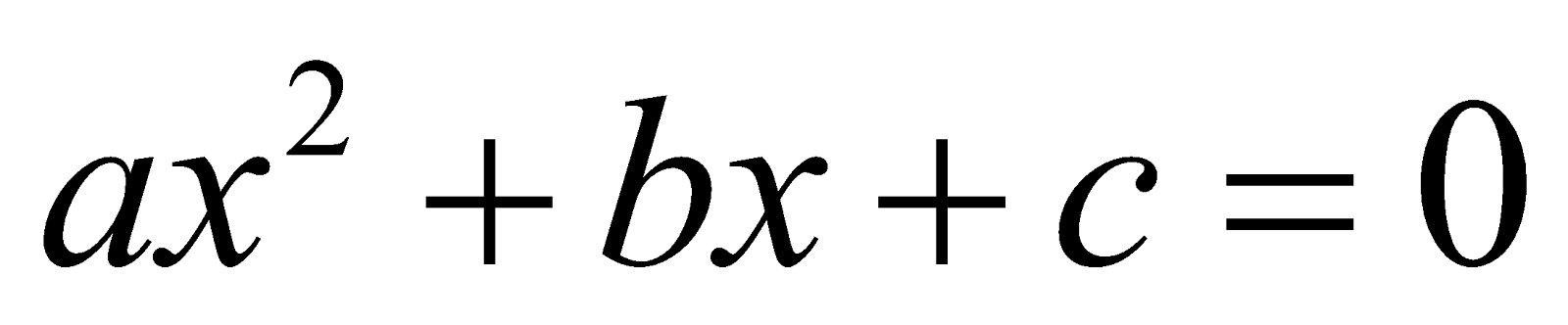 , say
, say  and
and . We draw an upward parabola showing the sign scheme as drawn in the figure.
. We draw an upward parabola showing the sign scheme as drawn in the figure.
No need to show y-axis. The sign-scheme illustrates that
and  if
if 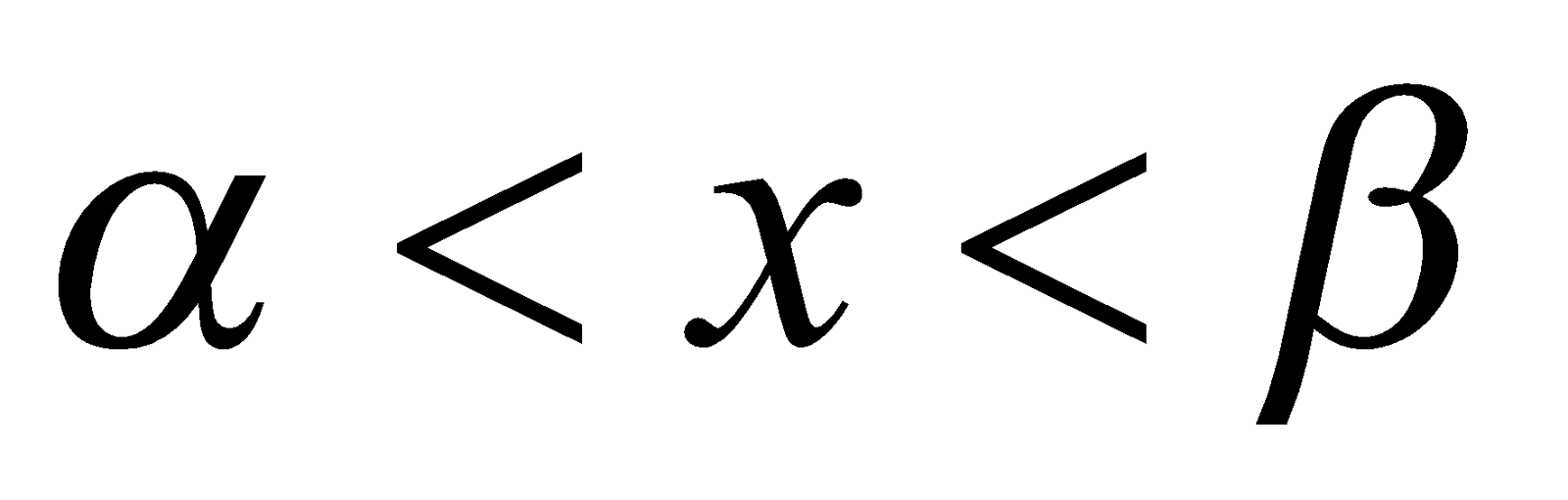
For example :
- We solve the inequality
.
Here D = 1 > 0
Now 

We draw the upward parabola with sign - scheme as shown in the figure.
Since, we have to solve  , we consider the interval, with negative sign, which represents,
, we consider the interval, with negative sign, which represents, 
Hence, the solution to the given inequality is 
- We solve the inequality
Here D = –23 < 0
Since, D < 0 

solution of  is
is  (i.e., no solution)
(i.e., no solution)
- We solve the inequality
, Here D = –11 < 0 Since, D< 0
. Hence solution set of the inequality
is
- We solve the inequality
. Here D = 5 > 0 we first convert the coefficient of x2 positive by multiplying it by –1.
Thus 
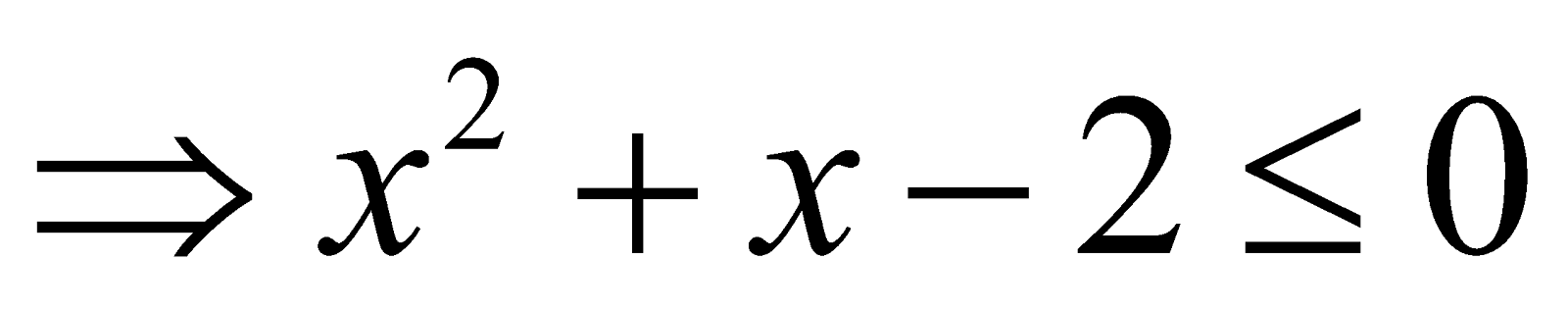

From the adjacent graph and sign-scheme.
- We solve the inequality
.
we have 
PROBLEM RELATED TO EXTREME VALUES OF QUADRATIC EXPRESSIONS
From the analysis of quadratic functions, we have
- If a > 0, then the minimum value of
is
and is attained when
So, 
- If a < 0, then the maximum value of f(x) = ax2 + bx + c is
and is attained when
So, 
For example :
- If
then we find the maximum value of (2 + 3x) (1 – x) the expression is f(x) = (2 + 3x)(1 – x) = 2 + x – 3x2. Here
. So the maximum value of
, which occurs at
- If
Then the minimum value of
is
(Here a > 0)
Now 
∴ Minimum value of  is 4 and it occurs at
is 4 and it occurs at 
PROBLEMS RELATED TO RANGE OF VALUES OF QUADRATIC RATIONALS
The range of values of quadratic rational  can be evaluated with the help of previous articles. It is illustrated in the following example :
can be evaluated with the help of previous articles. It is illustrated in the following example :
Example :
We find the range of values of  ,
, 
Let  . We express, it as a quadratic in x.
. We express, it as a quadratic in x.
Thus 
PROBLEMS RELATED TO LOCATING THE ROOTS OF QUADRATIC EQUATION UNDER GIVEN CONDITIONS
- Both the roots of equation
are greater than a given number m, if
,
and
- Both the roots of equation
are smaller than a given number M, if
,
and
- A given number k lies between the roots of
if
- Exactly one root of
lies between the given numbers p and q if
. But f(p) and f(q) are not simultaneously zero.
- Both the roots of
lie between two given numbers m and M, if
,
,
and
(assuming m < M)
For example :
Consider the quadratic equation  . We will find the values of parameter 'a' under various conditions :
. We will find the values of parameter 'a' under various conditions :
- If both the roots of given equation are greater than unity, then
,
and
The common values of a among above three solutions are 
Hence, both the roots of equation are greater than 1, if 
- If both the roots of given equation are smaller than unity, then
and
The common values of a are 
Hence, both the roots of given equation are smaller than 1, if 
- If one root of given equation is greater than unity and other is smaller than unity, then
Hence, 1 lies between the roots of the equation if 
- If exactly one root of given equation lies in the interval
(1, 3), then
Hence, exactly one root of the equation lies between
1 and 3, if
1 and 3, if
- If both the roots of given equation lie in the interval
then
and 

The common values of a among above four solutions are 
Hence, both the roots of equation lie between 1 and 3 if 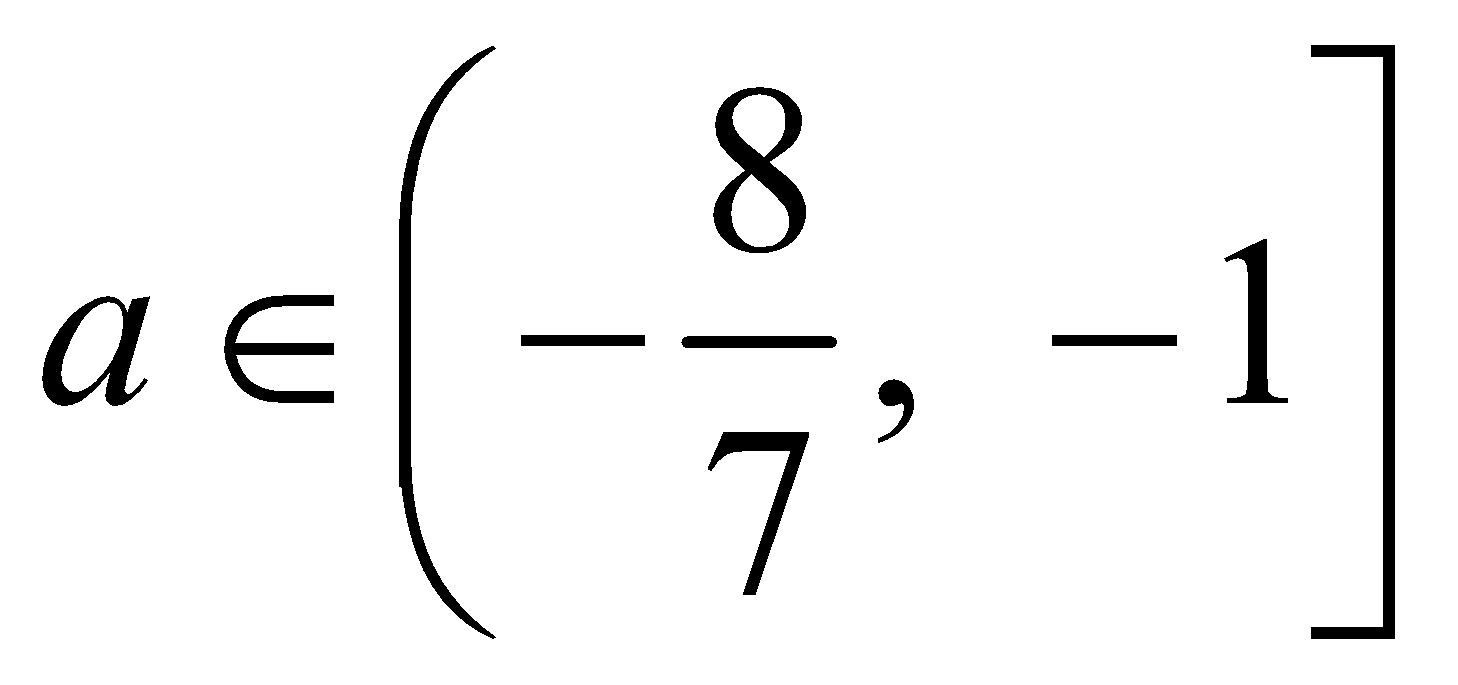
- If one root is greater than 3 and other root is smaller than 1, then
and
[
1 and 3 lie between the roots]
and 7a + 8 < 0
The common values of among above two solutions are 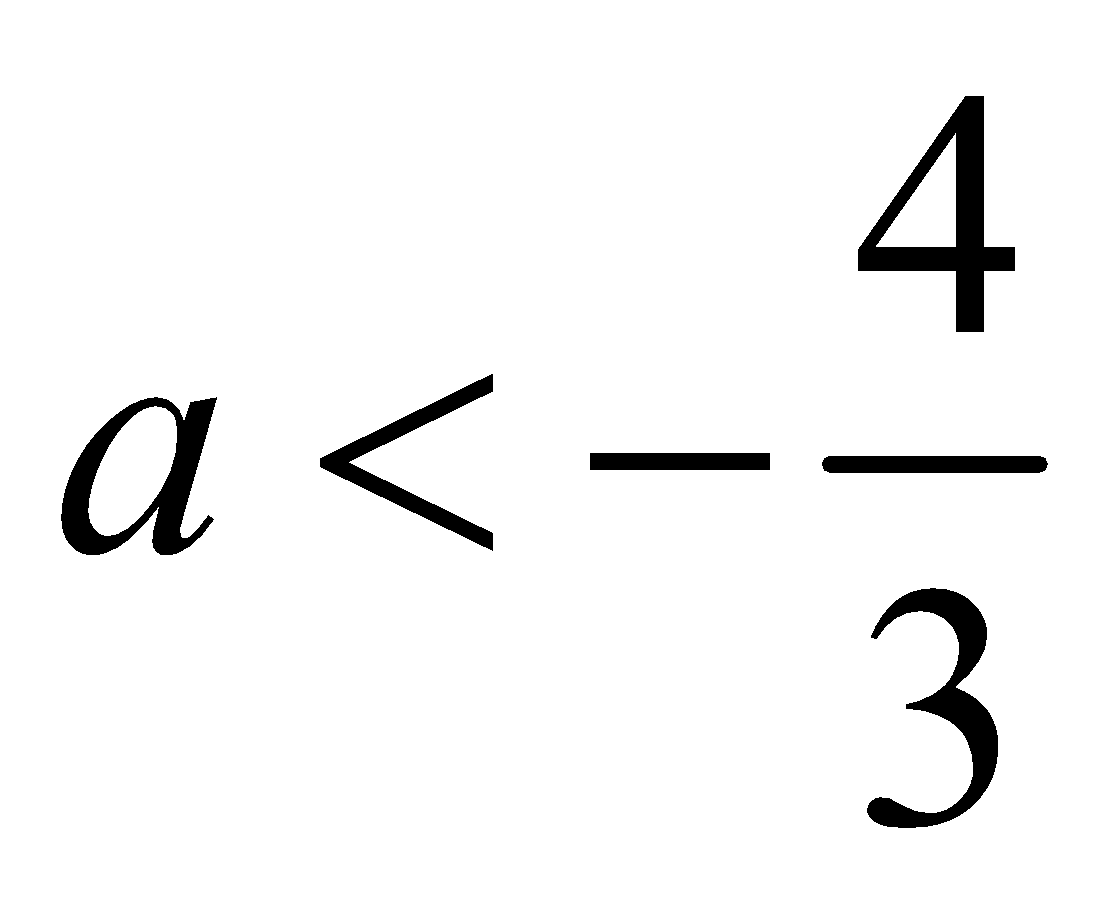
Hence, one root is greater than 3 and other root is smaller than 1 if 







