Sequences and Series | Mathematics Notes for IITJEE Main

SEQUENCES AND SERIES

DEFINITION

An arrangement of numbers < x1, x2,....., xn,.....> according to definite rule or a set of rules is called a SEQUENCE. The various numbers occurring in a sequence are called its terms. The nth term of the sequence is denoted by xn. The nth term is also called the GENERAL TERM of the sequence. For example,

1. The numbers  represent a sequence written according to the rule
2. The numbers represent a sequence written according to the rule
3. The numbers <1, 3, 5, 7, .......> represent a sequence written according to the rule
4. The numbers <1, 3, 7, 13, 21,....> represent a sequence written according to the rule
5. The numbers <1, 1, 2, 3, 5, 8,......> represent a sequence written according to the following set of rules

This sequence of numbers is called the Fibonacci sequence.

6. The numbers represent a sequence of successive approximations to the irrational number.
7. The numbers represent a sequence of successive approximations to the irrational number.
8. The numbers represent a sequence of prime numbers.

It is not always possible to write a specific formula in as in examples (6), (7) & (8).

SEQUENCE AS A FUNCTION ON THE SET OF NATURAL NUMBERS

We may define a sequence as a function whose domain is some subset of set of natural numbers N of the type {1, 2, 3,........n} = X (say) to other set  of number Y. f : X → Y

• The ordered set of images in Y given by {f(1), f(2), f(3)........f(n)} is the sequence.
• Sequence containing finite number of terms is called a FINITE SEQUENCE and it is INFINITE SEQUENCE if contains infinite number of terms.
• In the above function representation, the sequence {f(1), f(2), f(3),...} is called a REAL SEQUENCE if Y = R, i.e., f(1), f(2), f(3).......are real numbers and it is called a COMPLEX SEQUENCE if Y = C, i.e., f(1), f(2), f(3),.......are complex numbers. The terms of the sequence f(1), f(2), f(3)......are respectively called the first term , second term, third term and alternatively may be denoted by

etc.

METHODS OF DESCRIBING A SEQUENCE

• A sequence may be described by writing first few terms till the rule for writing down the other terms is evident.
• A sequence may be described by giving a formula for its general term (the nth term)
• A sequence may be described by specifying first few terms and a formula (or a set of formulae) giving a relation between successive terms. Such a formula is called RECURSIVE FORMULA (or RECURRENCE RELATION) see the example 5 previously.
• Some sequences may not be described by any rule

SERIES

If 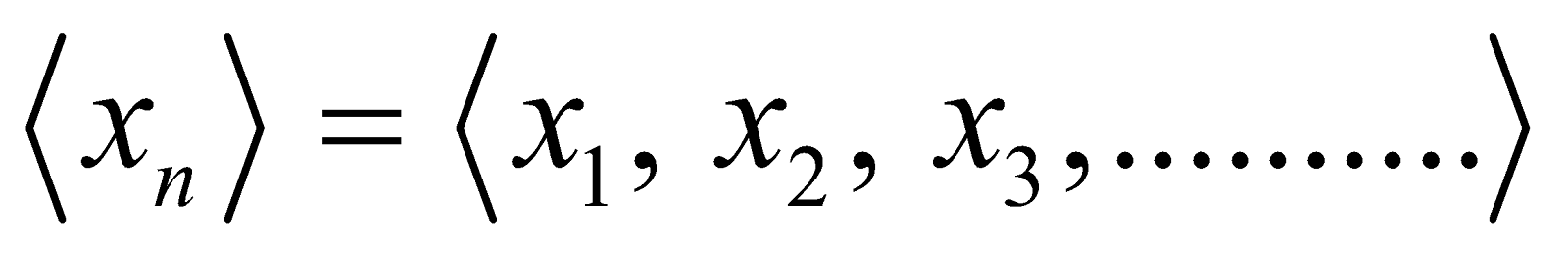is a sequence, then the expression x1 + x2 + x3 + ..... is called the SERIES associated with the given sequence.

Series is often represented in compact form, called sigma notation, using the Greek letter as means of indicating the summation involved.

Thus the series x1 + x2 + x3 + .............. + xn is abbreviated as

Note that series refers to the indicated sum and not to the sum itself. For example, 1 + 4 + 7 + 10 is a finite series of four terms. When it is asked to “find the sum of the series” then we need the number that results from adding the terms, so the sum of the series 1 + 4 + 7 + 10 is 22.

PROGRESSION

Sequences, following certain patterns are called progressions. In a progression, each term except the first progresses in a definite manner.

ARITHMETIC PROGRESSION (A.P.)

The sequence is called an arithmetic progression (A.P.) if

In general (The difference of successive term is constant).

Thus, A.P. is a sequence in which each term except the first is obtained by adding a fixed number (positive or negative) to the preceding term.

The constant difference d is called the common difference of the A.P. If the first term x1 of the A.P. be taken a. Then the standard form of A.P. is <a, a+d, a+2d,..........>

Formula for General Term of an A.P.

The nth term of the A,P., written in standard form is given by

Formula for Sum to n terms of an A.P.

The sum to first n terms of the Arithmetic series is given by

IMPORTANT CHARACTERISTIC OF A.P.

1. 
2. If nth term of any sequence is a linear in n, then the sequence is an A.P. If xn is of the form An + B, then the common difference is A.
3. If sum of n terms of any sequence is quadratic in n of the form An2 + Bn then the sequence is an A.P. and the common difference is 2A.
4. If <x1, x2, x3,.......,.......xn> is an A.P. Then
1. nth term xn is called the last term  of A.P. and denoted by l also,
2. 

That is the sum of terms equidistant from beginning and end is constant

3. is an A.P., where k is constant
4. is an A.P., where k is non zero constant
5. is an A.P., where k is non-zero constant.
6. is an A.P. for any p and q.
7. The k th term form end of an A.P. = (n+1–k)th term from beginning = a + (n – k) d.

Alternate, kth term from end of an A.P.

= l + (k – 1)  (–d), where l is the last term.

8. xm = , where
8. If be two different A.P.'s then

<x1 + y1, x2 + y2, x3 + y3,.........> is an A.P.

<x1 – y1, x2 – y2, x3 – y3,.........> is an A.P.

6. If three terms to be selected in A.P., choose them a – d, a, a + d
7. If four terms to be selected in A.P., choose them a - 3d, a - d, a + d, a + 3d
8. Three numbers a, b, c are in A.P. if and only if b – a = c – b, i.e., if and only if a + c = 2b

ARITHMETIC MEAN (A.M.) OF TWO TERMS A & B

If a, A, b are in A.P. then A is called ARITHMETIC MEAN of numbers a and b, we get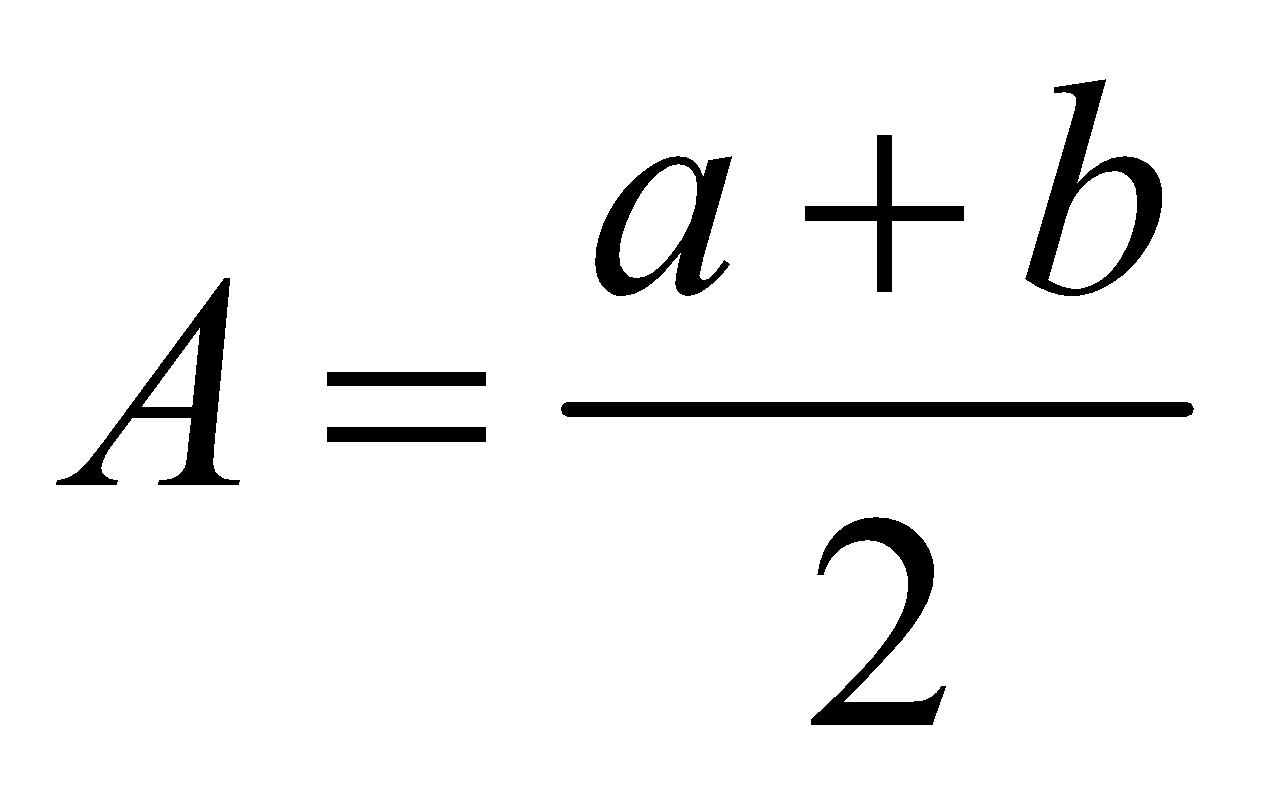

Inserting n Arithmetic Means between two terms a and b

Let be such that  a, A1, A2,......An, b is A.P.

Clearly

;    ;

..................... ,

..................... ;

We have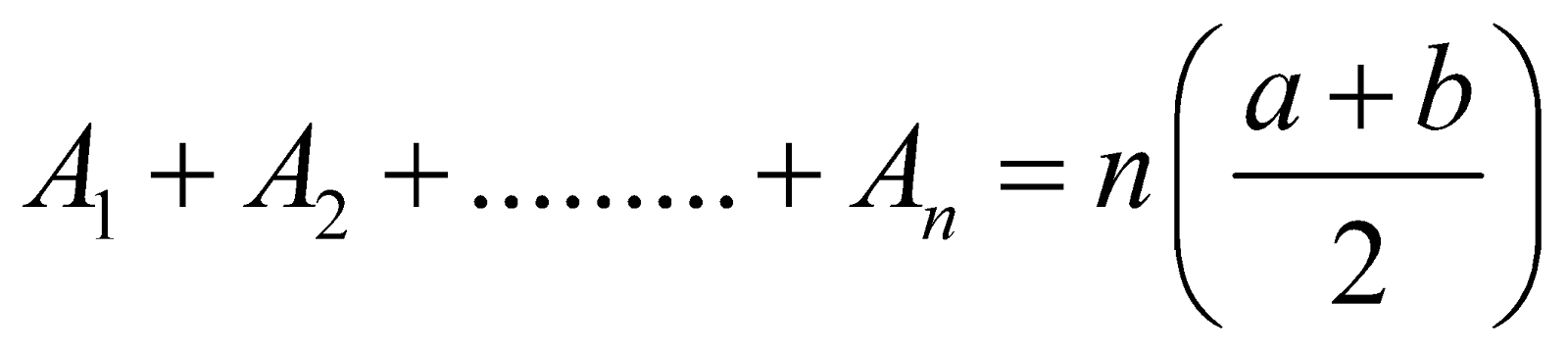

That is, Sum of n A.M. terms between a and b = n × A.M. of a and b.

GEOMETRIC PROGRESSION (G.P.)

The sequence is called a geometric progression (G.P.) if

, where none of x1, x2, ......, xn,...... is zero.

In general = constant (say, r),    

[The ratio of successive terms is constant]

This G.P. is a sequence in which each term except the first is obtained by multiplying the previous term by a non-zero constant.

The constant ratio r is called the common ratio of the G.P. If the first term x1 of the G.P. be taken as a, then the standard form of G.P. is <a, ar, ar2,........>

Formula for General Term of a G.P.

The nth term of the G.P. written in standard form is given by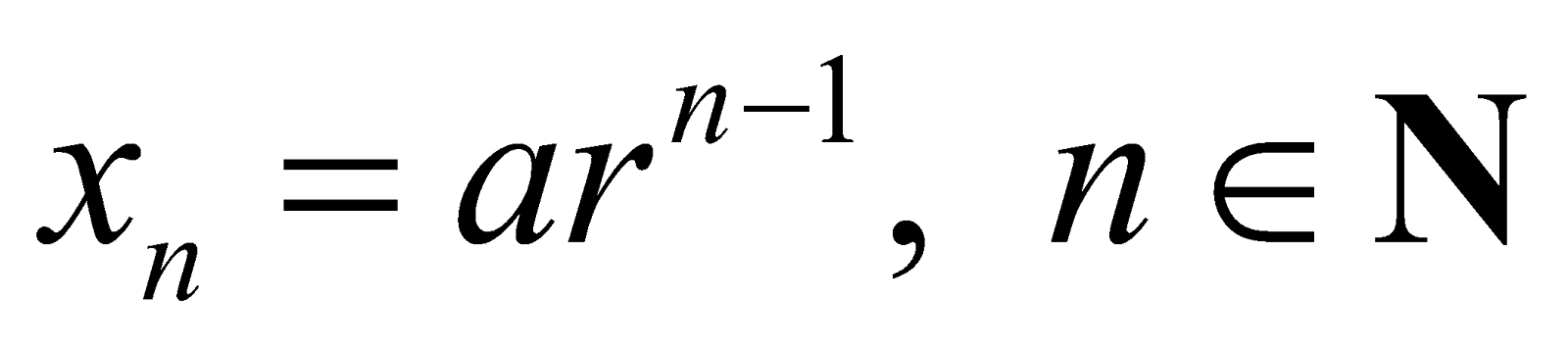

Formula for sum of n terms of a G.P.

The sum of first n terms of the geometric series a + ar + ar2 +.......... + arn – 1 is given by

and

Note :

• When r = 1, Sn = a + a + a + .... upto n terms = na.
• If l is the last term of the G.P., then

Formula for the Sum of infinite terms of a G.P.

If | r | <1, the sum of infinite terms (S) of the G.P. a + ar + ar2 + .............to infinity is

IMPORTANT CHARACTERISTICS OF G.P.

1. No term of a G.P. can be zero.
2. 
3. If is G.P. of n terms, then
1. 

That is the product of terms equidistant from beginning and end is constant

2. is a G.P.
3. is a G.P.,
4. <x1k, x2k, x3k,..........> is a G.P. (xi > 0)
5. is a GP.
6. is a GP. for any p and q
7. The kth term from end of a GP. = (n + 1 – k)th term from beginning = arn–k

Alternate, kth term from end of a G.P. , where l is the last term.

8. |xm| = , 0 < k < n – m
8. If be two different G.P.’s then and are G.P.’s
9. If is a G.P. of positive terms then is an A.P. and vice versa.
10. If is an A.P. then is a G.P. for some a > 0, a 1
11. If three terms to be selected in G.P. choose them.
12. If four terms to be selected in G.P. choose them
13. Three numbers a, b, c are in G.P. if and only if or if and only if b2 = a.c

GEOMETRIC MEAN (G.M.) OF TWO TERMS A AND B

If a, G, b are in G.P. (a and b are positive), then G is the GEOMETRIC MEAN of numbers a and b. We get  

Inserting n Geometric Mean between two terms a and b

Let a and b be positive numbers. Let G1, G2, ......, Gn be such that a, G1, G2, ......, Gn, b is a G.P.

Then

Thus the n geometric means between a and b are as follows :

; ;

We have,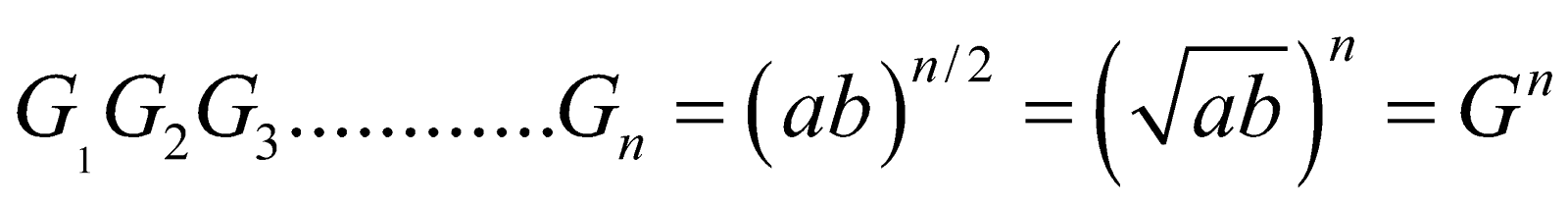

Product of n geometric mean terms between a and b = nth power of G.M. between a and b.

HARMONIC PROGRESSION (H.P.)

The sequence where each xi ≠ 0 is said to be a harmonic progression (H.P.), if the sequence formed by the reciprocals of its terms is an A.P. That is, the sequence is an A.P.

The standard form of H.P. is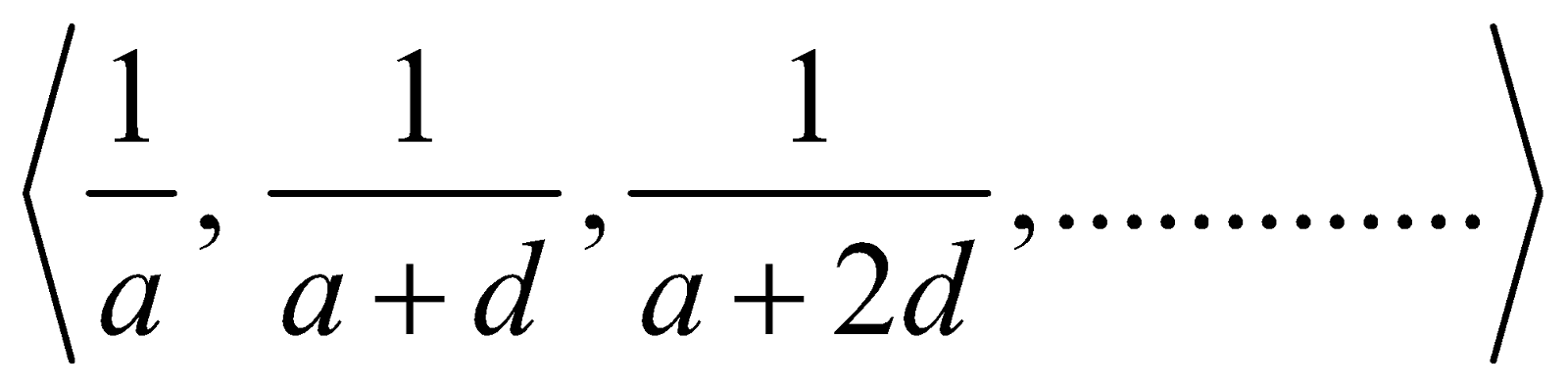

Note :

• Corresponding to every H.P. there is an A.P. and vice versa. Therefore, problems in H.P. can generally by solved with reference to the corresponding A.P.
• There is no formula for finding the sum of n terms of a H.P. The note 1 cannot be applied for summation of given terms of a H.P.
• Three numbers a, b, c are in H.P. if and only if are in A.P. i.e. =, i.e.
• No term of H.P. can be zero.

HARMONIC MEAN (H.M.) OF TWO NON-ZERO TERMS a AND b

If a, H, b are in H.P., then H is the HARMONIC MEAN of numbers a and b, we get

Inserting n Harmonic Means between two terms a and b

Let a and b be two non-zero numbers. Let be such that are in H.P.

Then is corresponding A.P.

Let d be the common difference of the A.P. Then

Thus, n harmonic means between a and b are as follows :

................................................

................................................

RELATIONS BETWEEN A.M. G.M. AND H.M.

If a and b are positive numbers, then

. We have

• A.M., G.M., H.M. are in G.P., i.e. G2 = AH
• A.M.  G.M. H.M., i.e., A G H.  Equality holds if and only if a = b
• If a1, a2, a3,.........., an be n positive numbers, then we define

A.M.   

G.M.   G = (a1 . a2. .......... an)1/n

H.M.  

We again have A > G > H. Equality holds if and only if a1 = a2= ........... = an.

ARITHMETICO-GEOMETRIC SEQUENCE

Consider an A.P.   

Consider a G.P.  

If a sequence is formed by multiplying the corresponding terms of above two sequences we get

This sequence is called an arithmetico-geometric sequence (A.G.S.)

The general term of this sequence is given by

Summation of n term of an A.G.S.

Let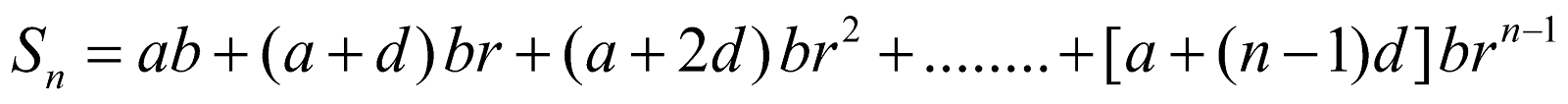

Subtract,

Summation of Infinite terms of an A.G.S.

If | r | < 1, then the sum S of infinite terms of the A.G.S given in standard form can be obtained as following

            

Sum to n terms of special Sequences

• Sum of first n natural numbers

• Sum of squares of the first n natural numbers

• Sum of Cubes of the first n natural numbers

• Sum of Sequences using Sigma Notation

If a sequence is characterized by <xn>

Then

If the general term xn is given by

, where a, b, c, d, k, are constants

Then

                

The last bracket being a G.P. whose sum can be found using standard formula.

• Difference Series

Consider 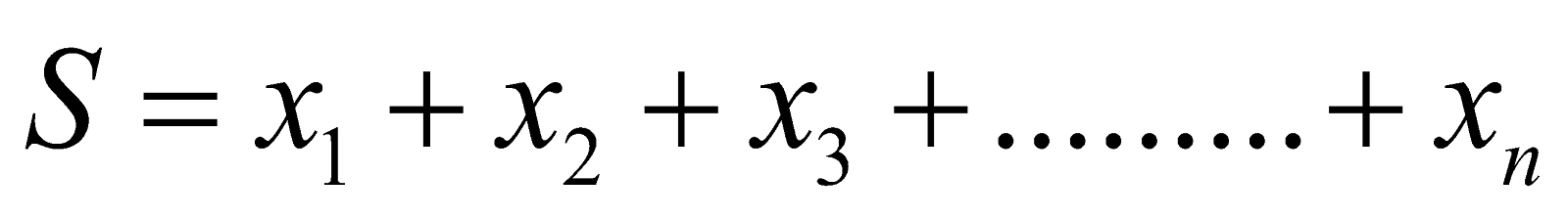 and let

If in an A.P. or G.P.

the series is termed as DIFFERENCE SERIES

To evaluate sum, we proceed as follows :

Where is the sum of series which is A.P. or G.P.

Hence xn may be evaluated and then the sum S may be calculated by

• Method of Difference

Consider the series

Suppose the general term xk can be expressed as

Then by putting k = 1, 2, 3, ….n we get

+.......+

or

       

Hence, the desired sum can be obtained by putting the values of f(n) and f(0) or f(1) and f(n + 1).

Mathematics Study Notes

• Sets, Relations and Functions
• Trigonometric Ratios and Identities
• Trigonometric Equations and Inequations
• Properties of Triangles, Height and Distances
• Principle of Mathematical Induction, Permutation and Combination
• Complex Numbers
• Quadratic Equations
• Linear Inequalities
• Sequences and Series
• Binomial Theorem
• Infinite Series
• Points & Straight Lines
• Pair of Straight Lines
• Circles
• Parabola
• Ellipse and Hyperbola
• Mathematical Reasoning
• Statistics
• Probability Basic
• Functions
• Inverse Trigonometric Functions
• Matrices
• Determinants
• Limits, Continuity and Differentiability
• Differentiation and Application of Derivatives
• Indefinite Integration
• Definite Integration and Applications
• Differential Equations
• Vector Algebra
• Three Dimensional Geometry
• Probability Advanced

Study Notes for JEE Main/JEE Advanced/BITSAT