SETS, RELATION AND FUNCTIONS
DEFINITION OF A SET
A well defined collection of distinct objects is called a SET.
The members of a set are called its ELEMENTS.
The sets are generally denoted by capital letters A, B, C...., X, Y, Z.
The elements of a set are generally denoted by small letters a, b, c,....., x, y, z.
The elements of a set are generally denoted by small letters a, b, c,....., x, y, z.
If x is an element of the set A, we write x∈A
If x is not an element of the set A, we write 
[The symbols  and
and  are read as “belongs to” and “ does not belong to” respectively]
are read as “belongs to” and “ does not belong to” respectively]
A well defined collection is such that given an object, it is possible to determine whether the object belongs to the particular collection or net, for example, the collection of all ministers in the cabinet of the Government of India, the collection of all subject taught to students of class XII, collection of all automobile companies which manufacture passengers’ car are sets. On the other hand, the collection of all intelligent students in a class, the collection of all tall girls in a senior secondary school, the collection of all difficult questions asked in Mathematics, Physics and Chemistry in IIT-JEE-2005 are not sets, since the words intelligent, tall, difficult are not well defined.
DESCRIPTION OF A SET
A set may be represented by either of the following two methods :
ROSTER METHOD OR TABULAR FORM
In this method a set is represented by listing all its elements separated by commas within braces {} For example,
- The set V of vowels in English alphabet is V = {a, e, i, o, u}
- The set E of even natural numbers is E = {2, 4, 6, 8,......}
- The set of letters forming the word SCHOOL is {S, C, H, O, L}
Note that every element of the set is listed only once and the order in which the elements are listed is immaterial.
PROPERTY METHOD OR SET BUILDER FORM
In this method, a, set is represented by stating a rule or a set of rules, which are satisfied by all the elements of the set and not by any other element outside the set. In general, we write S = { x : P (x)}
Which means that S is a set of elements, which satisfy the condition P(x).
[The symbol : or | is read as “such that”]
For example
V = { x : x is a vowel in the English alphabet}
E = {x : x is an even natural number}
A = { x : x is a letter of the word SCHOOL}
B = 
C = {x : x is a factor of 40, x ∈ N} = {1, 2, 4, 5, 8, 10, 20, 40}
D = 
TYPES OF SET
EMPTY SET OR NULL SET OR VOID SET
A set which does not contain any element is called the empty set.
A null set is denoted by φ or {}.
For example :
- C = {x : x is an even prime number greater than 2}
- D = {x : x is a married bachelor}
SINGLETON SET
A set containing only one element is called a singleton set.
For example :
- A = {4}
- B = {–7}
- C = {a}
- D = { x : x+4 = 0, x∈I}
- F = { x : x is the closest planet to the Earth}
- {0} is a singleton set
- φ is a void set but {φ} is a singleton set.
FINITE AND INFINITE SETS
A set which is empty or consists of a definite number of elements is called FINITE. If a set A consists of n distinct elements then we write n (A) = n or O (A) = n It is called the CARDINAL NUMBER, or CARDINALITY or ORDER of the set A. The cardinality of a void set is zero and the cardinality of a singleton set is 1. Other examples of finite set, are
- Set A of days of the week, n (A) = 7
- Set B of solutions of the equation x2– 4 = 0, n (B) = 2
- Set V of vowels in English alphabet, n(V) = 5
- Set M of all men is the world, n (M) may be a quite big number but it is a finite number although we do not know the exact number of elements in M.
A set whose elements cannot be counted is called an INFINITE SET.
For example,
N : the set of natural number = { 1,2,3.........}
Z or I : the set of integers = { ......., –3, –2, –1, 0, 1, 2, 3,....}
Q : the set of rational numbers 
R : the set of real numbers = { x : x is either a rational number or irrational number}
C : The set of complex numbers 
I+ : the set of positive integers
Q+ : the set of positive rational numbers
R+ : the set of positive real numbers
EQUAL AND EQUIVALENT SETS
Given two sets A and B. If every element of A is also an element of B and vice versa, the sets A and B are said to be equal and we write A = B. Clearly, A = B, if they have exactly the same elements.
(The symbol '⇒' stands for 'implies that']
For example :
- Let A ={1, 4, 5} and B = {4, 1, 5}, then A = B
- Let A = { x : 2 x 6, } and B = {2, 3, 4, 5, 6} then A = B
- Let A = { x : x is a prime number number less than 6} and B = {x : x is a prime factor of 30}, then A = B
- Let A = { x : x is a letter of the word ALLOY} and B = {x : x is a letter of the word LOYAL} then A = B
- Let A = {1, 2}, B = {1, 2, 2, 1} and C = { x : x2 – 3x + 2=0} then A = B = C.
Two finite sets A and B are said to be EQUIVALENT if they have the same number of elements, i.e. n(A) = n(B). We write A B
B
All equal sets are equivalent but all equivalent sets are not equal.
For example :
- A = {a, b, c} and B = {10, 20, 30} then A
B but A
B
then A
B but A
B
- { x : x2 –16 = 0, } and B = {x : x–16=0, } then A
B as well as A = B.
SUBSETS
If every element of a set A is also an element of a set B, then A is called a subset of B or A is contained in B and we write A B. [The symbol
B. [The symbol  is read as “a subset of” or “contained in”]
is read as “a subset of” or “contained in”]
Thus A B if x ∈ A ⇒ x ∈ B
B if x ∈ A ⇒ x ∈ B
If A B, then we also say that B is a SUPERSET of A and we write B
B, then we also say that B is a SUPERSET of A and we write B A (read as "B contains A").
A (read as "B contains A").
THEOREMS
, i.e. null set is subset of every set
, i.e. every set is subset of itself
For any set A, φ and A are called IMPROPER SUBSETS. All other subsets of A are called PROPER SUBSETS. If B is a proper subset of A, we write . [The symbol
. [The symbol  is read as “ is a proper subset of”]
is read as “ is a proper subset of”]
- For two sets A and B
[The symbol  is read as “if and only if” also written as iff or sometimes “implies and implied by”]
is read as “if and only if” also written as iff or sometimes “implies and implied by”]
- A finite set containing n elements has 2n subsets. However the number of proper subsets is 2n – 2.
Examples :
- If A = {2, 3, 4} and B = {1, 2, 3, 4], then
- If A = {a, b, c} then n (A) = 3. Hence A has 23 = 8 subsets, viz, φ; {a}; {b}; {c}; {a, b}; {b, c}; {c, a}; {a, b, c}. φ and {a,b, c} = A are improper subsets. All other are proper subsets.
- The set of irrational numbers, denoted by T, is composed of all other real numbers. Thus T = {x : x ∈ R and x ∉ Q}, i.e., all real numbers that are not rational. Members of T include
,
and π.
Some of the obvious relations among these subsets are:
N ⊂ Ζ ⊂ Q, Q ⊂ R, T ⊂ R, N ⊄ Τ.
INTERVALS AS SUBSETS OF R
Let a, b ∈ R and a < b. Then the set of real numbers {y : a < y < b} is called an open interval and is denoted by (a, b). All the points between a and b belong to the open interval (a, b) but a, b themselves do not belong to this interval.
The interval which contains the end points also is called closed interval and is denoted by [a, b]. Thus [a, b] = {x : a ≤ x ≤ b}.
We can also have intervals closed at one end and open at the other, i.e.,
[a, b) = {x : a ≤ x < b} is an open interval from a to b, including a but excluding b.
(a, b] = {x : a < x ≤ b} is an open interval from a to b including b but excluding a.
These notations provide an alternative way of designating the subsets of set of real numbers. For example, if A = (–3, 5) and B = [– 7, 9], then A ⊂ B. The set [0, ∞) defines the set of non-negative real numbers, while set (– ∞, 0) defines the set of negative real numbers. The set (-∞, ∞) describes the set of real numbers in relation to a line extending from -∞ to ∞.
On real number line, various types of intervals described above as subsets of R, are shown in the following figure :
Here, we note that an interval contains infinitely many points.
For example, the set {x : x ∈ R, – 5 < x ≤ 7}, written in set-builder form, can be written in the form of interval as (–5, 7] and the interval [– 3, 5) can be written in set-builder form as {x : – 3 ≤ x < 5}.
The number (b – a) is called the length of any of the intervals (a, b), [a, b], (a, b] or [a, b). The intervals (a, b] and [a, b) are also referred as semi-closed (or semi-open) intervals.
POWER SET
Let A is a given set. The collection of all the subsets of the set A is called the power set of A. It is denoted by P(A).
Hence, P(A) = {S : S A}
A}
For example : If A = {a, b, c} then
P(A) = {φ, {a}, {b}, {c}, {a,b} {b,c} {c,a} {a, b, c}}
Clearly if A is a finite set and n(A) = m, then n (P(A)) = 2m
UNIVERSAL SET
A set, which contains all sets under consideration as subsets is called the universal set. It is denoted by U. The choice of universal set is not unique. Different universal sets are used in different contexts.
COMPARABLE SETS
Two sets A and B are said to be comparable if  .
.
VENN DIAGRAM
Most of the relationship between sets can be represented by means of diagrams called Venn diagrams. In the Venn diagram the universal set U is represented by the interior of a rectangle. Other sets under consideration are represented by the interior of circles drawn inside the rectangle.
If a set A is a subset of a set B then the circle representing A is drawn inside the circle representing B.
OPERATIONS ON SETS
UNION OF SETS
Let A and B be two sets. The union of A and B is the set of all those elements which belong to A or B or A and B both. Symbolically we write A∪B which is read as “A union B” Thus
A∪B = {x : x A or x
A or x B} or x A∪B x A or x B
B} or x A∪B x A or x B
Also, 
In the Venn diagrams the shaded regions represent the union of sets A and B in different cases
The union of a number of sets A1, A2, A3, .........An, i.e. A1∪A2∪A3∪.......∪An is represented by
For example :
- If A = {1,2,3}; B={2,3,4,5}. Then A ∪ B = {1,2,3,4,5}
- If A = {a, e,i,o,u}; B= {e,o,u}. Then A ∪ B = {a, e,i,o,u}
- If A = {1,2}; B = {a,b,c} Then A ∪ B = {1,2,a,b,c}
- If A {x : x ∈ I+}; B{x : x ∈ I and x < 0} ;
Then A ∪ B { ..........4, 3, 2, 1, -1, -2, -3,....} = 
ALGEBRA OF UNION
Let A, B, C be any three sets defined in the universal set U, then
- Idempotent Law : A ∪ A = A
- Commutative Law : A ∪ B = B ∪ A
- Associative Law : (A ∪ B) ∪ C = A ∪ (B ∪ C)
- Identity Law : (i) A ∪ φ = A, (ii) A ∪ U = U
INTERSECTION OF SETS
Let A and B are two sets. The intersection of the sets A and B is the set of all those elements which belong to both A and B. Symbolically, we write A∩B, which is read as “A intersection B” Thus, A ∩ B = {x : x ∈ A and x ∈ B} or x ∈ A ∩ B ⇒x ∈ A and x ∈ B
Also,  .
.
In the following Venn diagrams, the shaded regions represent the intersection of sets A and B in different cases.
The intersection of a number of sets A1, A2, A3, ....., An i.e. A1∩ A2∩ A3∩..............∩ An is represented by  .
.
For example :
- If A = {2,4,7,10} and B = {1, 2, 3, 4}, Then A∩B = {2,4}
- If A = {x : x is a prime number} and B = {x : x ∈ N}
Then A∩B = {x : x is a prime number} = A. [Note that A ⊂ B]
- If A = {1,3,5,7,9,......}; B = {2,4.6,8,.....}, Then A ∩ B = φ.
ALGEBRA OF INTERSECTION
- Idempotent Law : A∩A = A
- Commutative Law : A∩B = B∩A
- Associative Law : (A∩B)∩C = A∩ (B∩C)
- Identity Law : (i) A∩φ = φ, (ii) A∩U = A
- Distributive law : (i) A∪(B∩C) = (A∪B) ∩ (A∪C) (ii) A∩(B∪C) = (A∩B) ∪ (A∩C)
DIFFERENCE OF SETS
Let A and B are two sets. The difference of the sets A and B, in this order, is the set of elements which belong to A but not to B. Symbolically, we write A – B and read as “ A difference B” Thus, A – B = { x : x ∈ A and x ∉ B}
Similarly, B – A = { x : x ∈ B and x ∉ A}
In the Venn diagram, A – B and B – A are shown by shaded regions.
For example :
If A = { 1, 2, 3, 4} and B = { 3, 4, 5, 6}
Then A – B = {1, 2} and B – A = {5, 6}
We note that A – B 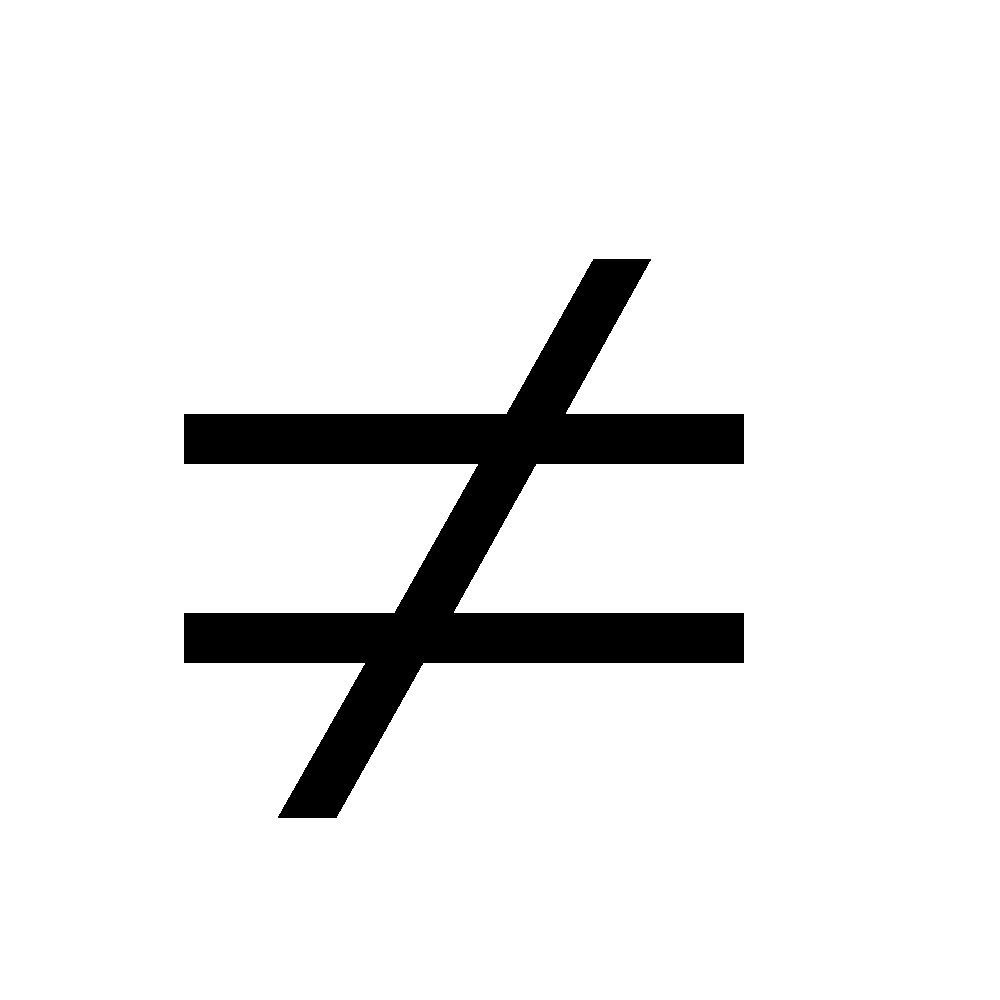 B – A
B – A
SOME IMPORTANT RESULTS
- A⊆A∪B
- B ⊆ A ∪ B
- A∩B⊆A
- A∩B⊆B
- If A⊆B, then (a) A∪B = B, (b) A∩B = A
- If A∩B = φ, then A and B are called DISJOINT SETS
- If A∩B ≠ φ, then A and B are called OVERLAPPING SETS.
- A – B⊆A, B – A ⊆ B
- A⊆BA – B = φ
- A – B ≠ B – A
- A – B = A – (A∩B)
- A – φ = A and A – A = φ
- A – (A – B) = A B
- A – B = B – A A = B
- A – B, B – A, A∩B are pairwise disjoint.
SYMMETRIC DIFFERENCE
If A and B are two sets, then the set, (A – B) ∪ (B – A) is called the symmetric difference of A and B and is denoted by A Δ B or A ⊕B
∴ A Δ B = {x : x ∈ A and x ∉B or x ∈ B and x∉A} = {x : x∉A∩B}
In the Venn diagram the shaded area represents A Δ B
For example :
Let A = {1, 2, 3} and B = {2, 3, 4, 5} then
A – B = {1} and B –A = {4,5}
∴ A Δ B = (A–B) ∪ (B–A) = {1, 4, 5}
COMPLEMENT OF A SET
Let U be the universal set and A is a subset of U. The complement of the set A, denoted be A’ or Ac is the set of all those elements of U which are not the elements of A.
Thus, A’ or Ac = { x : x ∈ U and x ∉A} = U – A
Thus, A’ or Ac = { x : x ∈ U and x ∉A} = U – A
∴ x ∈ A’ ⇔ x∉A
The complement of the set A is shown by shaded area in the following Venn diagram.
ALGEBRA OF COMPLEMENT
- A∩A’ = φ
- A ∪ A’ = U
- U’ = φ
- φ’ = U
- (A’)’ = A
- A ⊆ B ⇔ B’ ⊆ A’
- A – B = A∩B’
- B – A = B∩A’
- A – B = B’ – A’
- De morgan’s laws
- (A∪B)’ = A’∩B’
- (A∩B)’ = A’∪B’
- A – (B∪C) = (A– B) ∩ (A–C)
- A – (B∩C) = (A–B) ∪ (A–C)
SOME IMPORTANT RESULTS
- A Δ B = (A–B) ∪ (B–A) = (A∪B) – (A∩B)
- A – B = A ⇔ A ∩ B = φ
- (A–B) ∪ B = A∪B
- (A – B) ∩ B = φ
- A ∩ (B – C) = (A∩B) – (A∩C)
- A ∩ (BΔC) = (A ∩ B) Δ (A∩C)
(5) and (6) do not hold for union of sets.
, where P(A) is the power set of A
VERY IMPORTANT THEOREMS ON CARDINAL NUMBERS
Let A, B, C are finite sets in a finite universal set U. Then
- n (A ∪ B) = n (A) + n (B) – n (A ∩ B)
- n (A ∪ B) = n(A) + n (B)
A and B are disjoint non void sets.
- n (A∪B∪C) = n (A) + n (B) + n (C) – n (A∩B) – n (B∩C) – n (C∩A) + n ( A∩B∩C)
The results (1) and (3) can be extended to any number of sets.
- n (A–B) = n (A) – n (A ∩ B) = n (A ∩ B’)
- n (A Δ B) = n (A) + n (B) – 2 n (A∩B)
- n(A’) = n (U) – n (A)
- n (A’∪B’) = n (U) – n (A∩B)
- n (A’∩B’) = n (U) – n (A∪B)
- Let n (A) = p and n (B) = q
Then min {n(A∪B)} = max {p,q} and
max {n (A∪B)} = p + q
min { n (A∩B)} = 0 and max {n (A∩B)} = min {p, q}
- If A1, A2, ......, Am are disjoint sets, then
CARTESIAN PRODUCT OF SETS
Ordered Pair : A pair of objects, listed in a specific order, is called an ordered pair, for example (a, b) is an ordered pair of two elements a and b, a is called the FIRST ELEMENT and b, the SECOND ELEMENT.
Two ordered pairs (a, b) and (c, d) are equal if any only if a = c and b = d.
Cartesian product of Sets : Let A and B are two non-empty sets. The set of all ordered pairs (a, b) of elements a ∈ A and b ∈ B is called the Cartesian product of sets A and B and is denoted by A × B. Thus A × B = {(a, b) : a ∈A, b ∈ B}
For example :
If A = {1, 2, 3} and B = {a, b}, then
- A × B = {(1, a)}, (1, b), (2, a), (2, b), (3, a), (3, b)}
- B × A = {(a, 1)}, (a, 2), (a, 3), (b, 1), (b, 2), (b, 3)}
- A × A = {(1, 1)}, (1, 2), (1, 3), (2, 1), (2, 2), (2, 3),(3, 1), (3, 2), (3, 3)}
- B × B = { (a, a), (a, b), (b, a) (b, b)}
Note :
- If at least one of A or B is empty set then A×B = φ
- A × B ≠ φ iff A ≠ φ and B ≠ φ
- In general A × B ≠ B × A
- If A and B are finite sets, then n (A×B) = n (A). n (B)
- If A and B are non-empty sets and either A or B is an infinite set, then A×B is an infinite set
- If A = B, then A×B is expressed as A2. Thus A2 = A×A
- We can also define, in a similar way, ordered triplets. If A, B, and C are three sets, then (a, b, c), where a ∈A, b ∈ B and c ∈ C, is called an ordered triplet. The Cartesian product of sets A, B and C is defined as
A × B × C = {(a, b, c,) : a ∈ A, b ∈ B, c ∈ C}.
An ordered pair and ordered triplet are also called 2-tuple and 3-tuple, respectively. In general, if A1, A2,.....An are n sets, then (a1, a2,........an) is called an n-tuple where. ai∈Ai, i = 1, 2......., n and the set of all such n-tuples, is called the Cartesian product of A1, A2, .......An. It is denoted by A1×A2×........×An. Thus
A1×A2×.....×An = {(a1, a2,........an) : ai∈Ai,  }.
}.
SOME IMPORTANT THEOREMS
- A × (B∪C) = (A×B) ∪ (A×C)
- A×(B∩C) = (A×B) ∩ (A×C)
- A× (B–C) = (A×B) – (A×C)
- If A and B are two non-empty sets, then A×B = B×A ⇔ A=B
- If A ⊆ B, then A×A ⊆ (A×B) ∩ (B×A)
- A⊆ B ⇒A × C ⊆ B×C for any set C
- A ⊆ B and C⊆ D ⇒ A×C ⊆ B × D
- (A×B) ∪ (C×D) ⊆ (A∪ C)×(B∪D)
- (A×B) ∩ (C×D) = (A∩C) × (B∩D)
- (A×B) ∩ (B×A) = (A∩B) × (B∩A)
- Let A and B be two non-empty sets having n elements in common, then A×B and B×A have n2 elements in common.
RELATIONS
Let A and B be two non-empty sets. Then a relation (BINARY RELATION) R from A to B is a subset of A×B. That is, R is a relation from A to B ⇔ R⊆A × B
If R ⊆ A×A, the R is said to be a relation on A.
If (a, b) ∈R, then we write aRb and we say a is R related to b. Thus, (a, b) ∈R ⇔ aRb.
If  , then we say that a is not related to b.
, then we say that a is not related to b.
Example :
- If A = {3, 5} and B = {2, 4}, then A× B = {(3,2), (3,4), (5,2), (5,4)}
Let R be a relation “is greater than” from A to B,
That is aRb ⇔ a > b, a ∈ A, b ∈ B
Then, 3R2, 5R2, 5R4
∴ R = {(3,2), (5,2), (5,4)}. Clearly 
The visual representation of a relation is an arrow diagram as shown below:
- If A = {2, 3, 5, 6} and R be a relation “divides” on A that is aRb ⇔ a divides b then 2R2, 2R6, 3R3, 3R6, 5R5, 6R6
∴ R = {(2,2), (2,6), (3,3), (3,6) (5,5) (6,6} ⊆ A×A
The corresponding arrow diagram is as follows :
DOMAIN AND RANGE OF A RELATION
Let A and B are two sets and R is a relation from A to B, i.e. R ⊆ A × B
The set of all the first components of the ordered pairs of the relation R is called the DOMAIN of R. Thus Domain of R = {a ∈ A : (a, b) ∈ R for some b ∈ B}
The set of all the second components of the ordered pairs of the relation R is called the RANGE of R. Thus, Range of R = {b ∈ B : (a, b) ∈ R for some a ∈ A}
Clearly domain of R ⊆ A and range of R ⊆ B
The set B is called the CO-DOMAIN of R
Example :
- If A = {1,2,3} and B = {a, b, c} let R = {(1,a) (1,c), (2, b)
Then domain of R = {1, 2} range of R = {a, b, c}
- Let R be a relation on the set N of natural numbers defined by a + 3b = 12.
Then R = {(9, 1), (6, 2), (3, 3)}
[The values of a can be obtained by giving the values
b = 1, 2, 3. Clearly b 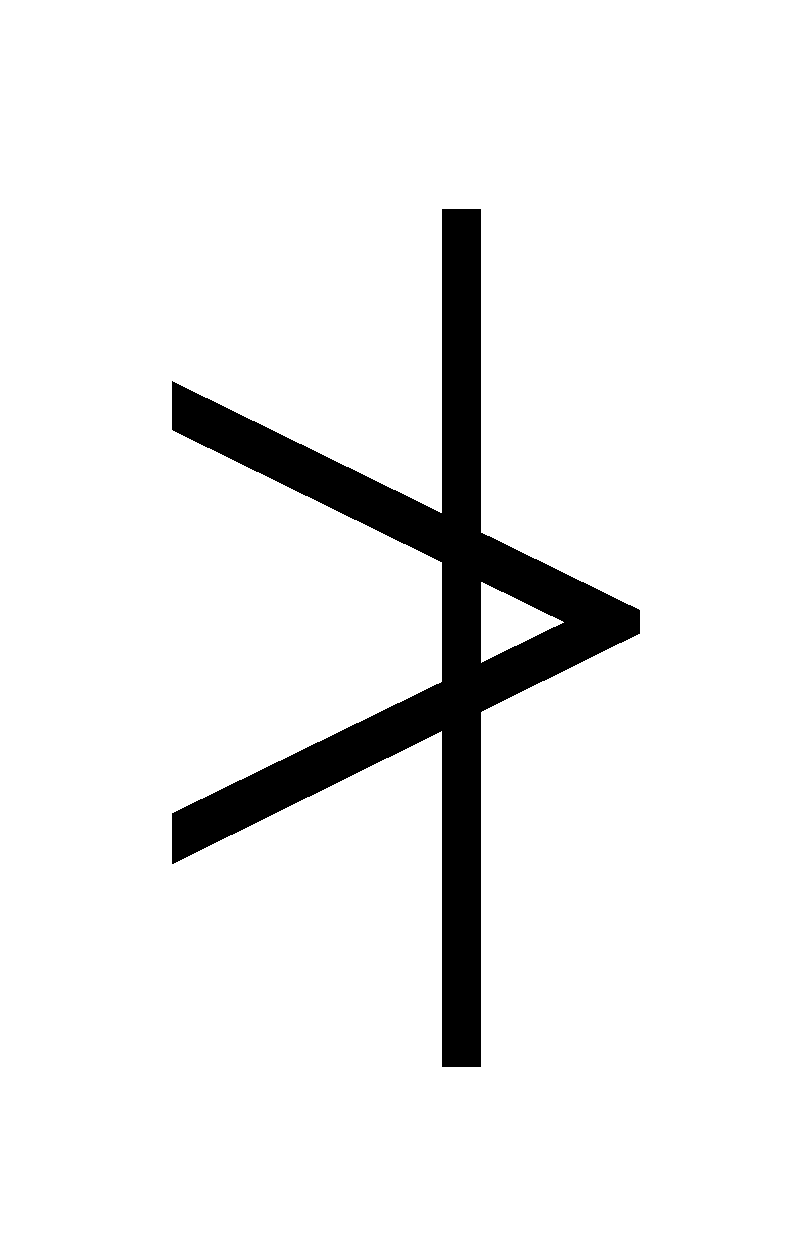 3, otherwise a becomes zero or negative]
3, otherwise a becomes zero or negative]
∴ domain of R = {9, 6, 3} and range of R = {1, 2, 3}
NUMBER OF RELATIONS
Let A contains m elements and B contains n element. Then A×B contains mn elements. Hence, A×B has 2mn subsets. That is the total number of relations from A to B are 2mn. The relations φ (called a VOID RELATION) and A × B (called an UNIVERSAL RELATION) are said to be TRIVIAL RELATIONS from A to B.
INVERSE RELATION
The inverse relation of a relation R is the set obtained by reversing each of the ordered pairs of R and is denoted by R–1. Clearly, if R ⊆ A×B then R–1⊆ B × A. We write
R–1 ={(y, x) : (x, y) ∈ R}
∴ (x, y) ∈ R ⇔ (y, x) ∈R–1. It is clear that domain of
R–1 = range of R and range of R–1 = domain of R also. (R–1)–1 = R
R–1 = range of R and range of R–1 = domain of R also. (R–1)–1 = R
Example :
- Let A = {1, 2, 3} and B = {a, b, c}
If R = {(1, a), (2, a), (3, b), (3, c)} ⊆ A × B
Then R–1 = {(a, 1), (a, 2), (b, 3), (c, 3)} ⊆ B×A
- Let A be set of first ten natural numbers.
Define a relation R on the set A by (a, b) ∈ R ⇔ a + 2b = 10
We have b = (10-a)/ 2. Clearly a must be even.
Also A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
∴ 2R4, 4R3, 6R2, 8R1
Thus, R = {(2, 4), (4, 3), (6, 2), (8, 1)} and R–1 = {(4, 2), (3, 4), (2,6) (1,8)}
TYPES OF RELATIONS ON THE SET A
Let A be a set and R is a relation on A, i.e. R ⊆ A × A. Then we define
VOID RELATION
If R = φ , then R is called a void relation on A.
UNIVERSAL RELATION
If R = A×A, then R is called an universal relation on A.
IDENTITY RELATION
A relation R is defined as an identity relation if R = {(a, a) : a ∈ A}. Thus in an identity relation on A, every element of A is related to itself only. Identity relation on A is also denoted by IA. Thus IA = {(a, a) : a ∈ A}
Example : If A = {1, 2, 3}, then IA = {(1, 1), (2, 2), (3,3)}
REFLEXIVE RELATION
A relation R is said to be a reflexive relation on A if every element of A is related to itself.
Thus R is reflexive ⇔ (a,a) ∈R, i.e. aRa a∈A
a∈A
[The symbol is read as “for every element”]
is read as “for every element”]
IMPORTANT POINTS
- Identity relation on a non-void set A is always reflexive on A. However, the converse need not be true.
- Universal relation on a non-void set A is reflexive
- In null set φ , every relation is reflexive.
- The relation R on N defined by (a, b)∈R ⇔ a = b is reflexive.
- The relation R on the set of real numbers R defined by (a, b) ∈R ⇔ a ≥ b
a, b ∈R, is reflexive for a ≥ a
a ∈R, hence aRa. [The relation > is not reflexive]
- Let X be a non-void set, then a relation R on P(X), the power set of X such that (A, B) ∈R ⇔ A ⊆ B is reflexive for A ⊆ A
A [every set is subset by itself]
- Define a relation R on the set L of all straight lines in a plane such that
(l1, l2) ∈R ⇔ l1is parallel to l2; l1 and l2 are two straight lines, is reflexive, for lRl for every straight line l [every straight line is parallel to itself]
The relation “perpendicular to” is not reflexive.
SYMMETRIC RELATION
A relation R on a set A is defined as a symmetric relation if (a,b) ∈R ⇒ (b, a) ∈R That is,
aRb ⇒ bRa, where a, b∈A.
aRb ⇒ bRa, where a, b∈A.
IMPORTANT POINTS
- Identity relation and universal relation on a non-void set are symmetric.
- In the null set every relation is symmetric.
- The relation R on N, defined by aRb ⇔ a = b is symmetric.
- The relation R on R defined by aRb ⇔ a ≥ b is not symmetric [for if a ≥ b ⇒ b
a]
- The relation R on P(X) for a non-empty set X, defined by ARB ⇔ A ⊆ B is not symmetric.
- The relation R on the set L defined by l1Rl2 ⇔ l1 is parallel to l2 is symmetric.
- The relation R on the set L defined by l1Rl2 ⇔ l1 is perpendicular to l2 is symmetric.
- A reflexive relation on the set A is not necessarily symmetric.
- A relation R on a set A is symmetric iff R = R–1.
TRANSITIVE RELATION
A relation R on a set A is defined as a transitive relation if (a,b) ∈R and (b,c) ∈R ⇒ (a,c) ∈R
That is, aRb and bRc ⇒ aRc, where a, b, c, ∈A.
IMPORTANT POINTS
- Identity and Universal relations on a non-empty set are transitive.
- Every relation defined on the null set φ is transitive
- The “perpendicularity” relation of the set L is not transitive.
ANTISYMMETRIC RELATION
A relation R on a set A is antisymmetric if (a,b) ∈R and (b,a) ∈R ⇒ a = b
If (a, b) ∈ R and (b, a) ∉R, then still R is an antisymmetric relation.
IMPORTANT POINTS
- Identity relation on a non-empty set is antisymmetric
- Universal relation on a set A containing at least two distinct elements cannot be anti-symmetric.
- The relation R on R defined by aRb ⇔ a ≥ b is antisymmetric [For a ≥ b and b ≥ a ⇒ a =b]
- The relation R on P(X) for a non-void set X defined by ARB ⇔ A⊆B is antisymmetric.
- The relation R on N defined by aRb ⇔ a divides b is antisymmetric. However, the relation is not antisymmetric on I.
EQUIVALENCE RELATION
A relation R on a set A is an equivalence relation if and only if
- R is reflexive, i.e, aRa
a∈A
- R is symmetric, i.e., aRb ⇒ bRa
- R is transitive, i.e., aRb and bRc ⇒ aRc
PARTIAL ORDER RELATION
A relation R on a set A is a partial order relation if and only if.
- R is reflexive, i.e. aRa
a∈A
- R is antisymmetric i.e., aRb and bRa ⇒ a = b
- R is transitive, i.e., aRb and bRc ⇒ aRc.
RELATION OF CONGRUENCE MODULO (m)
Let m be a fixed positive integer. Two integers a and b are said to be “congruent modulo m” if a – b is divisible by m. We write a ≡ b (mod m)
Thus. a ≡ b (mod m) [Read as “ a is congruent to b modulo m”]
iff a – b is divisible by m; a, b ∈ Ι.
iff a – b is divisible by m; a, b ∈ Ι.
For example :
(i) 25 ≡ 5 (mod 4) because 25–5 = 20 is divisible by 4.
(ii) 23 ≡ 2 (mod 3) because 23 –2 = 21 is divisible by 3
(iii) 203 (mod 5) because 20 – 3 = 17 is not divisible by 5
The relation “congruence modulo m” is an equivalence relation on I.
SOME THEOREMS ON EQUIVALENCE RELATION
- If R and S are two equivalence relations on a set A, then R∩S is also an equivalence relation on A.
- If R and S are two equivalence relations on a set A, then R∪S is not necessarily an equivalence relation
- If R is an equivalence relation on a set A, then R–1 is also an equivalence relation on A.
COMPOSITION OF RELATIONS
Let R be a relation from set A to the set B and S be another relation from set B to the set C. Then we define a relation SoR (Read as “R composite S”) from A to C such that (a, c) ∈ SoR ⇔∃ b ∈ B such that (a, b) ∈ R and (b,c) ∈ S
[The symbol ∃ is read as “there exists”]
Clearly, aRb and bSc ⇒ a SoRc
Example :
Let A = {1, 2, 3} B = {x, y}, C = {a, b, c}
Let R = {(1, x), (1,y), (3, y)} ∈A×B
S = {(x,a), (x,b), (y,b), (y,c)} ⊆ B×C
Then SoR = {(1,a), (1,b), (1,c), (3,b), (3,c)} ⊆ A × C
Because (1,x) ∈ R and (x,a) ∈ S ⇒ (1,a) ∈ SoR, etc.
PARTITION OF A SET
Let S be a non-empty set and A1, A2,......be non-empty subsets of S. Then the set P given by P = {A1, A2, ......} is called a partition of the set S, provided
- A1∪A2∪........= S, i.e.
Ai = S
- For any two subsets Ai and Aj of S, Ai
Aj = φ
i.e. Ai  Aj = φ, i
Aj = φ, i j, Ai, Aj ∈ P
j, Ai, Aj ∈ P
Example :
- Let S = {1, 2, 3, 4, 5, 6, 7}. Suppose A1 = {1, 5}, A2 = {2, 4,7}, A3 = {3, 6}
Clearly 
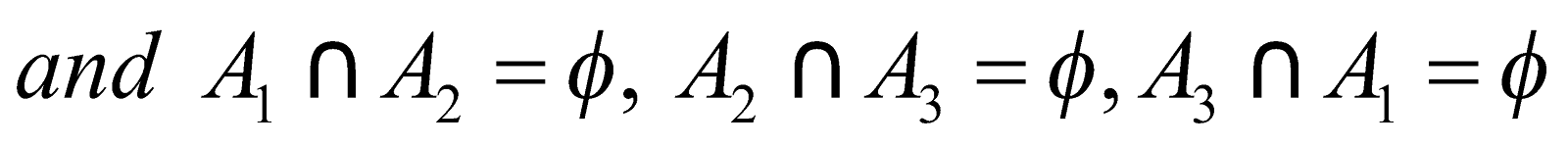
- All partitions of the set {a, b, c,} are
ONE-ONE CORRESPONDENCE
If A and B are two sets such that each element of A corresponds to one and only one element of B, and conversely, each element of B corresponds to one and only one element of A, then we say that there is one-one correspondence between the elements of A and the elements of B.
For example :
- Let
then there is one-one correspondence between the elements of A and their reciprocals in B and vice versa.
- There is one-one correspondence between the set of real numbers R and the points on a straight line.
FUNCTION OR MAPPING
If A and B are two non-empty sets, then a function or mapping or map from A to B is a subset f of A × B such that for every x ∈ A there is a unique y ∈ B, and the ordered pairs (x, y) ∈ f.
In other words, a function f is a relation from a non-empty set A into a non-empty set B such that domain of f is A and no two ordered pairs in f have the same first component. Clearly, every function is a relation but every relation is not a function.
If f is a function from A into B, then we write (x,y) ∈ f as f (x) = y, where x ∈ A and y ∈ B. y is called the IMAGE of x under f and x is called the PRE-IMAGE of y under f. The function f from A into B is denoted by f :  .
.
For example :
Let 
let us define following relations from A to B
In R1 every element of A occurs once and only once as the first element in the ordered pairs of R1, hence R1 is a function. We say that a is the image of 1; b is the image of 3 and c is the image of 2 and we may write
f (1) = a, f (2) = c and f (3) = b
1, 2 and 3 are pre-images of a, c and b respectively.
R2 is a function
In this case ‘a’ is the image of each of 1, 2 and 3, thus
f (1) = a, f (2) = a and f (3) = a
R3 is not a function as 1 occurs twice as the first elements in ordered pairs of R3.
R4 is not a function as 3 does not occur as the first element in any of the ordered pairs of R4.
KINDS OF FUNCTIONS
- One-to-one Function (or injective function)
A function f :  is called one-one mapping if every distinct element of A has a distinct image in B.
is called one-one mapping if every distinct element of A has a distinct image in B.
Thus, a function f : is one-one if
is one-one if 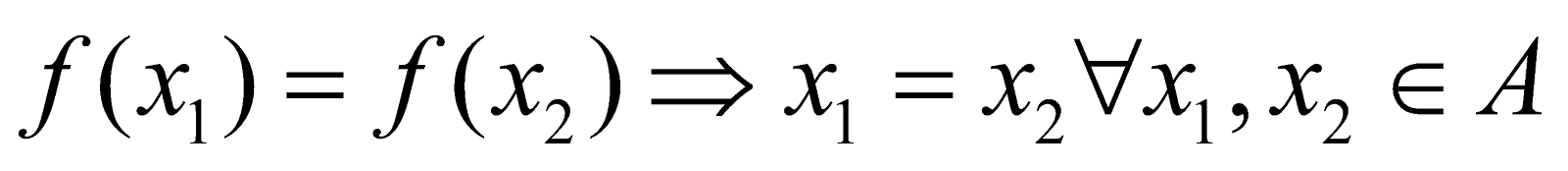
Alternatively, 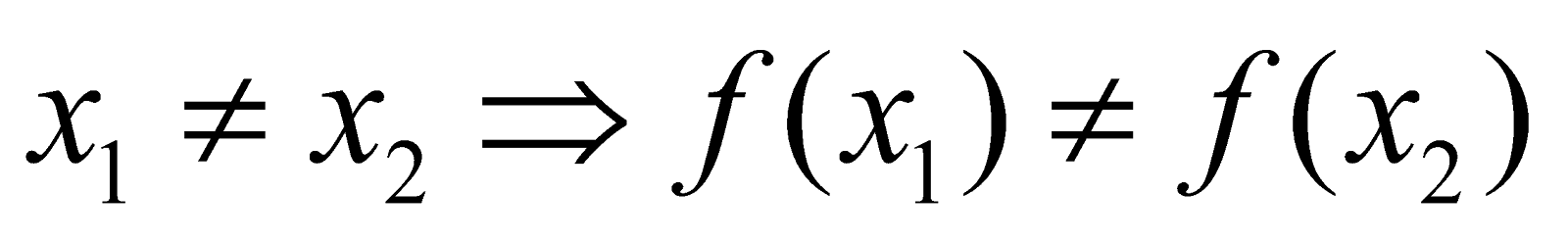
- Many-one Function : A function f :
is many-one if two or more different elements of A have the same image in B.
Thus, f : is many-one if
is many-one if
or  for some
for some 
- Onto or Surjective Function : The function f :
is said to be an onto function if every element of B is image of at least one element of A. That is, if for each
, there exists at least one
such that f(x) = y, then f is an onto function.
Thus, for a surjective function f, Range of f = codomain (B)
- Into Function : If the function f :
is such that there is at least one element of B which is not the image of any element of A, then f is called an into function.
For an into function f, Range of f  codomain (B)
codomain (B)
Example : Various combinations are shown in the following Venn diagrams.
- Bijective function : A function f :
is a bijective function if f is one-one as well as onto, i.e. f is injective and surjective both.
Composition of functions
Let A, B, C be three sets and f :  , g :
, g :  be two functions.
be two functions.
Define a function go f :  such that go f (x) = g ( f(x)) for all x ∈A.
such that go f (x) = g ( f(x)) for all x ∈A.
Since f (x) ∈B ∴ g ( f (x)) ∈ C.
The function go f is called the composition of f and g
[see also the composition of relations]
NOTE : You will study functions in great details in the chapter of functions in calculus.
IMPORTANT RESULTS
If A and B are two finite sets having m and n elements respectively, then
- Total number of functions from the set A to the set B = nm
- The number of one-one (injective) functions from A to B
= - If n = m, then every one-one function is a bijective function, thus, the number of bijective functions from A to B, provided n = m is n! = m!
- The number of onto (surjective) functions from A to B
=







