TRIGONOMETRIC RATIOS AND IDENTITIES
ANGLES
An angle is formed by the rotation of a ray in a plane, around the end point called the VERTEX. The original position of the ray is called the INITIAL SIDE
The final position of the ray after rotation is called the TERMINAL SIDE of the angle
The revolving ray is called the GENERATING LINE of the angle.
By convention, an angle is considered positive if it is generated by counter-clockwise motion of the revolving ray and the angle is regarded as negative if the motion is in clockwise direction.
The angle between two perpendicular lines is called a RIGHT ANGLE.
MEASUREMENT OF ANGLES
There are three principal system for measuring angles.
SEXAGESIMAL OR DEGREE SYSTEM (ENGLISH SYSTEM)
A right angle is divided into 90 equal parts. Each part is said to be one degree (1°). A degree is divided into 60 equal parts and each part is called a minute (1’). A minute is again divided into 60 equal parts and each part is called a second (1”). Thus 1 right angle = 90 degrees (90°)
1° = 60 minutes (60’)
1’ = 60 seconds (60”)
CENTESIMAL SYSTEM OR GRADE SYSTEM (FRENCH SYSTEM)
A right angle is divided into 100 equal parts Each part is said to be 1 grade (1g). Each grade is divided into 100 equal parts called a minute 1'. Each minute is divided into 100 equal parts called a second 1"
Note that minutes and seconds of sexagesimal system are not the same as the centesimal minutes and seconds.
CIRCULAR SYSTEM OR RADIAN SYSTEM
We know that for any circle, other than a point circle, the ratio of the circumference to its diameter is always constant. This constant is an irrational number denoted by π, whose value is 3.1415926536 [approximately  , correct upto 2 decimal places] Hence,
, correct upto 2 decimal places] Hence,
We define a RADIAN (1c) as the measure of an angle at the centre of a circle subtended by an arc equal in length to the radius of the circle.
For a general angle,
Thus, if in a circle of radius r, an arc of length l subtends an angle θ radians at the centre, then  .
.
Clearly, one complete revolution of initial side traverses an angle of  radians.
radians.
In general the angle θ radian is symbolically denoted by θc But the system is so frequently used that we omit the symbol (c) and the angle θ is always understood to be θ radian.
RELATION BETWEEN THREE SYSTEMS
Let D be the number of degrees, G the number of grades and C the number of radians of an angle AOB. For one complete rotation the angle subtended is 360° and 2π radian.
Also, 1 radian = = 57° 17’ 45’’ (approx)
= 57° 17’ 45’’ (approx)
We therefore get  ....(i)
....(i)
Similarly, 100 grades = 1 rt. angle = 90°
From (i) and (ii),  .
.
IMPORTANT NOTE
- The sum of interior angles of a polygon of n-sides = (n – 2) × 180º = (n – 2) π
- Each interior angle of a REGULAR polygon of n-sides =
- The sum of exterior angles of a polygon of any number of sides = 360º = 2π
TRIGONOMETRIC FUNCTIONS OR TRIGONOMETRIC RATIOS (T-RATIOS)
Suppose that in a right angled triangle ABC, ∠BAC = θ.
We define the following trigonometric ratios for the angle θ.
We define the following trigonometric ratios for the angle θ.
DOMAIN AND RANGE OF TRIGONOMETRIC FUNCTIONS
The sin θ function is defined for all real values of θ. Hence the domain of sin θ is set of real numbers R.
Further for any value of θ, sin θ can take value between –1 and 1 only, including –1 and 1, i.e., –1 ≤ sin θ ≤ 1. Hence, the range of values of sin θ is [–1, 1].
Following table provides the range and domain for all trigonometric functions.
BASIC FORMULAE OF TRIGONOMETRIC FUNCTIONS
- sin θ . cosec θ = 1 or
- cosθ . sec θ = 1
or 
- tan θ . cot θ = 1 or
SIGN OF TRIGONOMETRIC FUNCTIONS
Two perpendicular lines intersecting at a point O divide a plane in 4 right angles, each is called a quadrant. If θ be the angle that a line OA subtends with the initial line OX, anticlockwise then.
In I Quadrant, 0° < θ < 90°
In II Quadrant, 90° < θ < 180°
In III Quadrant, 180° < θ < 270°
In IV Quadrant, 270° < θ < 360°
The following table illustrates the sign of various trigonometric functions in all the four quadrants
I II III IV
sin θ + + – –
cos θ + – – +
tan θ + – + –
cot θ + – + –
sec θ + – – +
cosec θ + + – –
More precisely, we can discuss the way of increase and decrease of trigonometric functions as described in the following tables :
PERIODIC FUNCTIONS
A function f is said to be periodic if there exists a real number
T > 0 such that f (x + T) = f (x) for all x. T is called the period of the function.
T > 0 such that f (x + T) = f (x) for all x. T is called the period of the function.
All trigonometric functions are periodic functions with following periods.
For sin θ, cos θ, sec θ, and cosec θ, the period = 2π. For
tan θ and cot θ the period = π
tan θ and cot θ the period = π
THEOREM : If f(x) is a periodic function with period T, then f (ax + b) is a periodic function with period 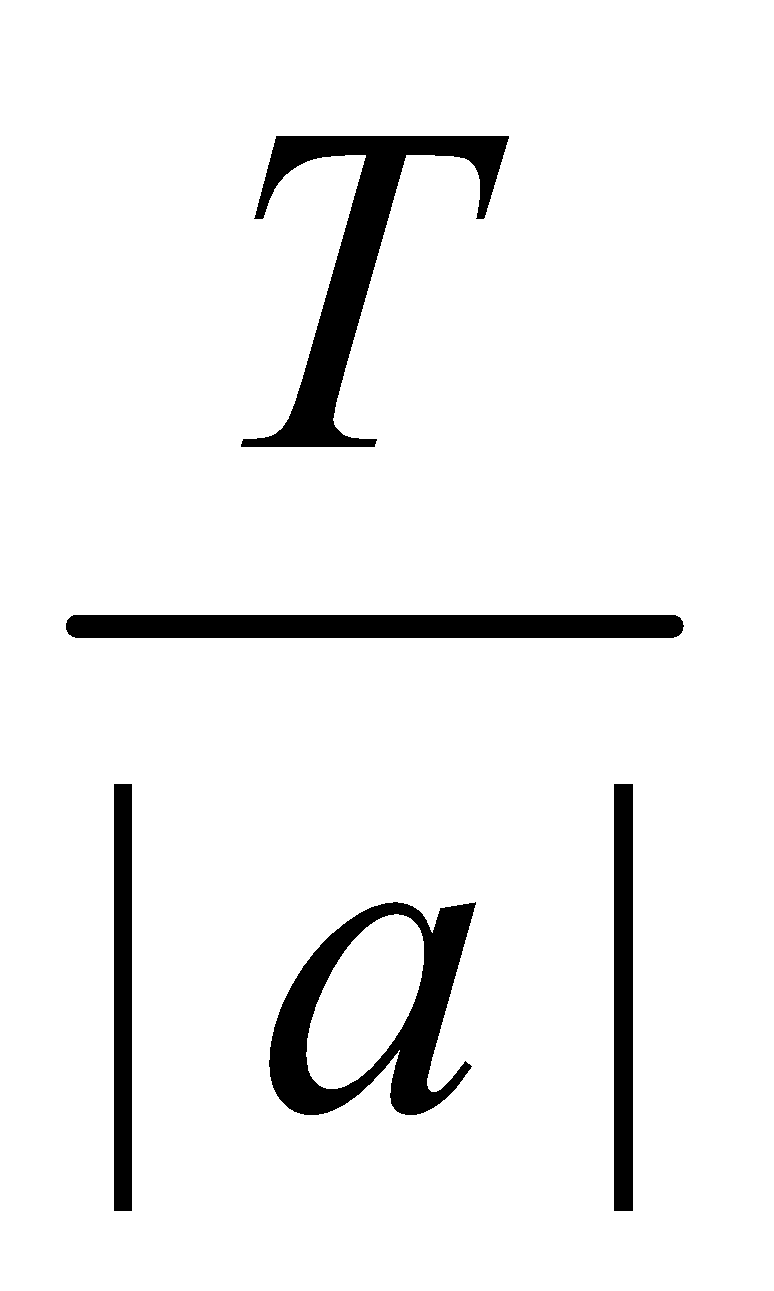
For example :
Period of sin θ is 2π
Period of sin 2θ is
Period of sin 2θ is
Period of 
Period of 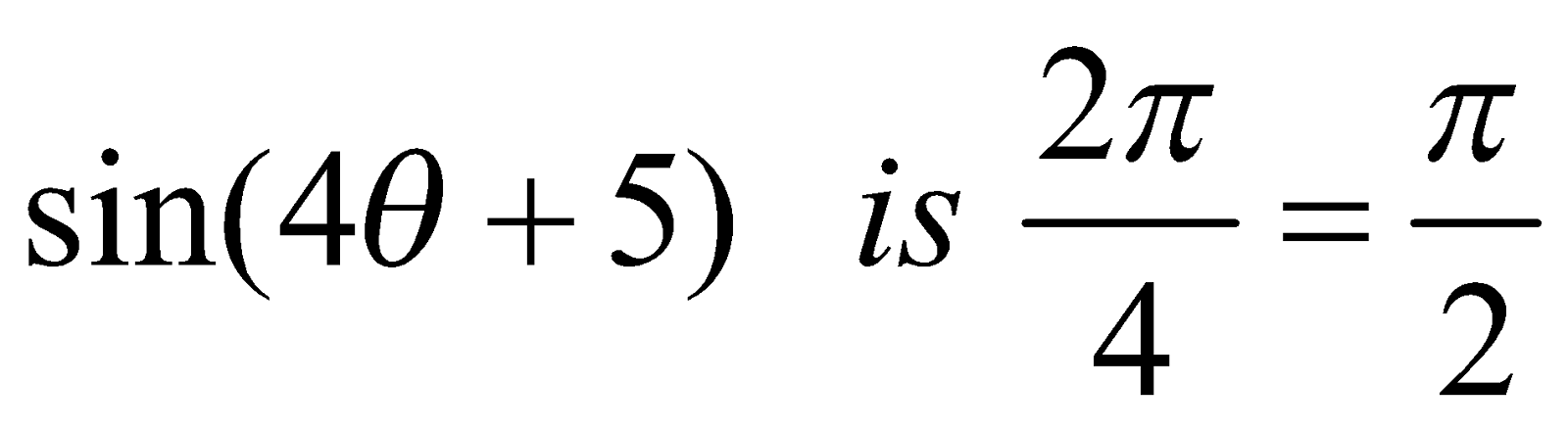 ....... etc.
....... etc.
PERIOD OF SOME IMPORTANT TRIGONOMETRIC FUNCTIONS
- Periods of sinnθ, cosnθ, secnθ, and cosecn θ = 2π if n is odd and π if n is even
- Periods of tannθ,cotnθ, = π, n even or odd.
- Periods of |sinθ|, |cosθ|, |tanθ|, |cot θ|, |secθ|, |cosec θ|= π
- Periods of |sin θ| + |cos θ|, |tan θ| + |cot θ|, |sec θ| + |cosec θ| are
TRIGONOMETRIC RATIOS OF COMPOUND ANGLES
- Conversion Table for T-Ratios of –θ in terms of T-Ratios of θ.
sin (– θ) = – sin θ, cos (– θ) = cos θ,
tan (– θ) = – tan θ cot (– θ) = – cot θ,
sec (– θ) = sec θ, cosec (– θ) = – cosec θ
- Conversion Table for T-Ratios of
in terms of T-Ratios of θ
- Conversion Table for T-Ratios π ± θ in terms of T-Ratios of θ
sin (π − θ) = sin θ sin (π + θ) = − sin θ
cos (π − θ) = – cos θ cos (π + θ) = − cos θ
tan (π − θ) = – tan θ tan (π + θ) = tan θ
cot (π − θ) = – cot θ cot (π + θ) = cot θ
sec (π − θ) = – sec θ sec (π + θ) = − sec θ
cosec (π − θ) = cosec θ cosec (π + θ) = − cosec θ
- Conversion Table for T-Ratios of
in terms of T-Ratios of θ.
- Conversion Table for T-Ratios of 2π ± θ in terms of T-Ratios of θ.
We can write the results of allied angles in case of sin, cos and tan in a generalised form as following :
- sin nπ = 0
- cos nπ = (–1)n
- tan nπ = 0
- sin (nπ + θ) = (–1)n sin θ
- cos (nπ + θ) = (–1)n cos θ
- tan (nπ + θ) = tan θ
- sin
=
cos θ, where n is odd
- cos
=
sin θ, where n is odd
- tan
= –cot θ, where n is odd
To find ratios for nπ – θ and  , replace θ by –θ in all of the above.
, replace θ by –θ in all of the above.
TRIGONOMETRIC RATIOS OF SUM AND DIFFERENCE OF ANGLES
,
,
Generalisation :
- sin (A1 + A2 + ...... + An) = cos A1 cos A2 ...... cos An (S1 – S3 + S5 – ....)
- cos (A1 + A2 + ...... + An) = cos A1 cos A2 ...... cos An (1 – S2 + S4 – S6 + ....)
- tan (A1 + A2 + ...... + An) =
where S1 = Σ tan A , S2 = Σ tan A1 tan A2,
S3 = Σ tan A1 tan A2 tan A3 and so on.
FORMULAS TO TRANSFORM PRODUCTS INTO SUM AND DIFFERENCE
- 2 sin A cos B = sin(A+B) + sin (A – B)
- 2 cos A sin B = sin (A+B) – sin (A – B)
- 2 cos A cos B = cos (A+B) + cos (A – B)
- 2 sin A sin B = cos (A – B) – cos (A + B)
FORMULAS TO TRANSFORM SUM OR DIFFERENCE INTO PRODUCT
TRIGONOMETRIC FUNCTIONS OF MULTIPLE AND SUB-MULTIPLE ANGLES
;
;
;
;
;
FORMULAS FOR LOWERING THE DEGREE OF TRIGONOMETRIC FUNCTIONS
CONDITIONAL TRIGONOMETRIC IDENTITIES
If A + B + C = 180° (or π), or A, B, C are angles of a triangle. Then
- sin (A + B) = sin (π – C) = sin C, etc .
GRAPHS OF TRIGONOMETRIC FUNCTIONS
- Graph of y = sin x
- Graph of y = cos x
- Graph of y = tan x
- Graph of y = cot x
- Graph of y = sec x and y = cosec x
- Graph of y = 3 cos 2x
In a similar way graph of other similar trigonometric functions can be obtained
Since the period of cos x is 2π. Therefore the period of cos 2x is . Also –3 ≤ 3 cos 2x ≤ 3. The graph of y = 3 cos 2x is drawn for a period, i.e. for 0 ≤ x ≤ π. The complete graph is simply the repetition of this portion.
TABLE FOR THE VALUES OF TRIGONOMETRIC RATIOS OF SOME IMPORTANT ANGLES
TABLE -1
TABLE - 2
EXPRESSIONS OF SIN AND COS
AND COS IN TERMS OF Sin A
IN TERMS OF Sin A
We have 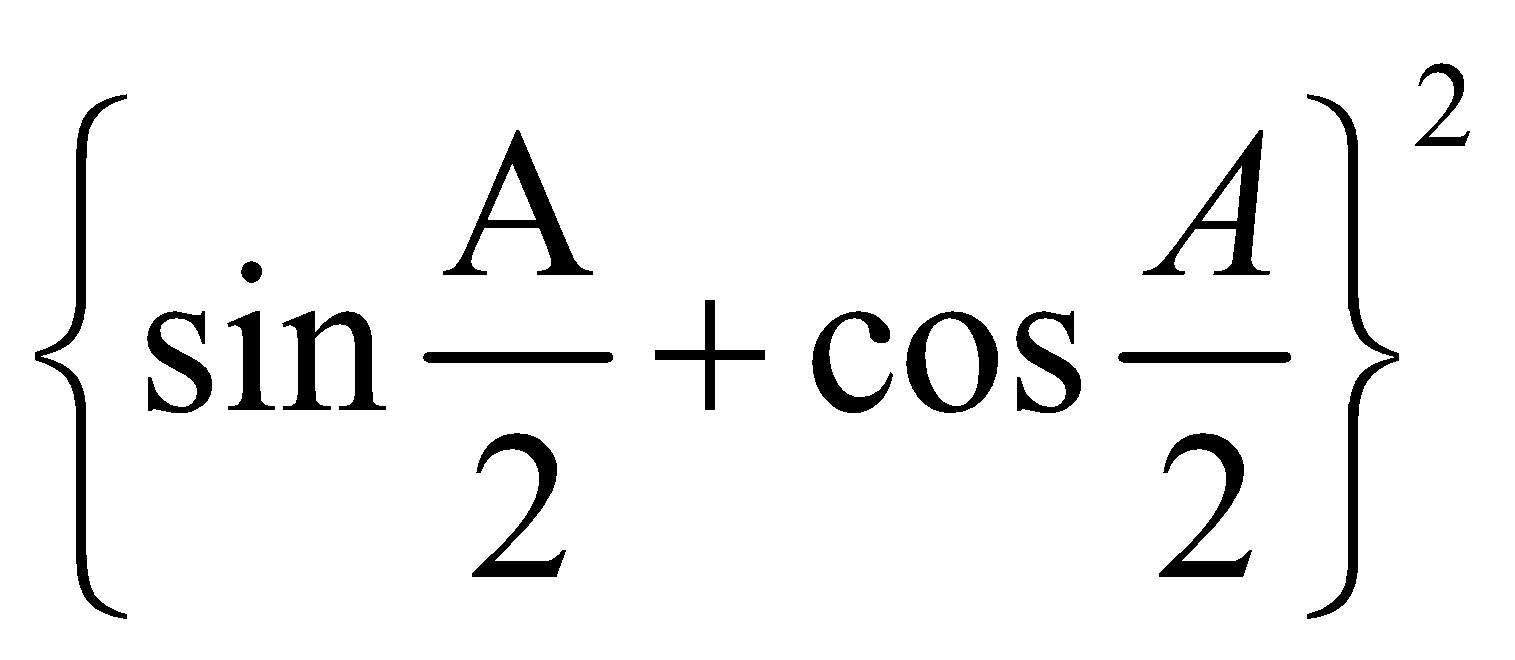 = 1 + sinA and
= 1 + sinA and  = 1 – sinA
= 1 – sinA
So that  =
=  and
and 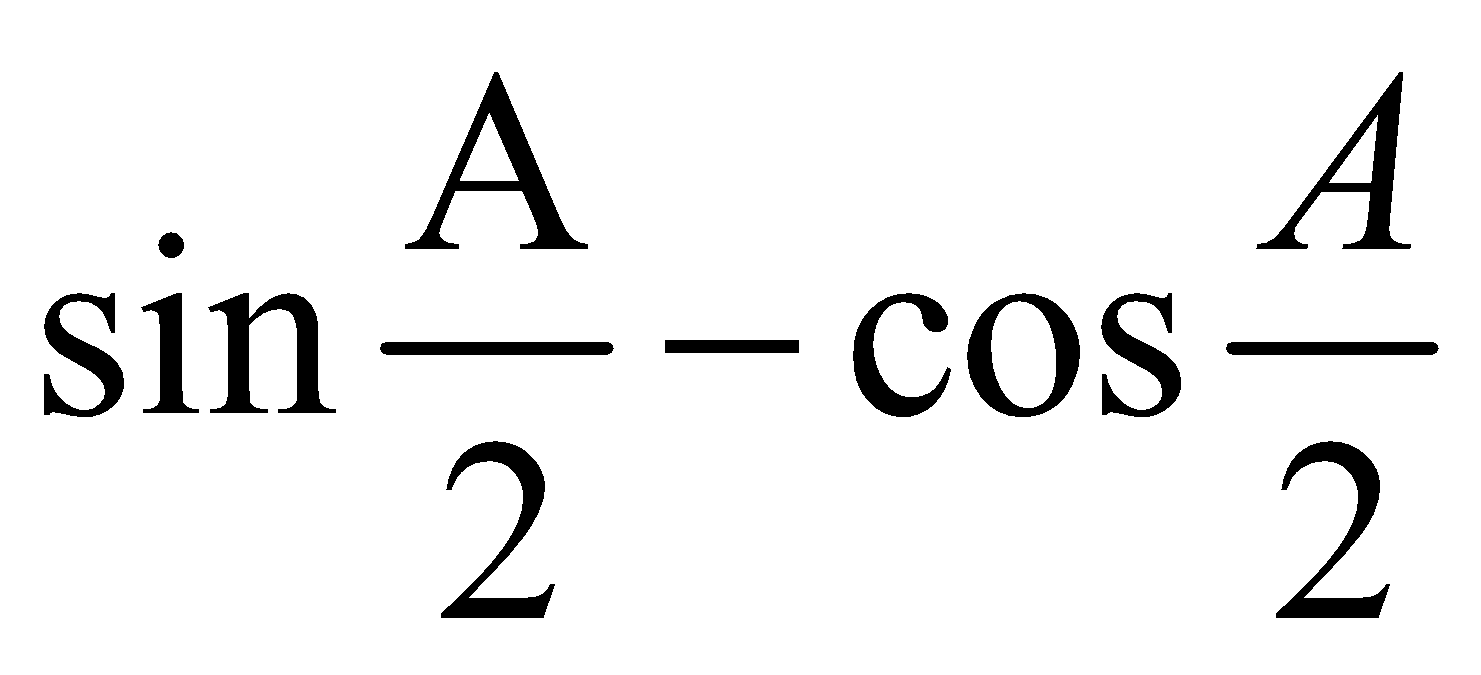 =
= 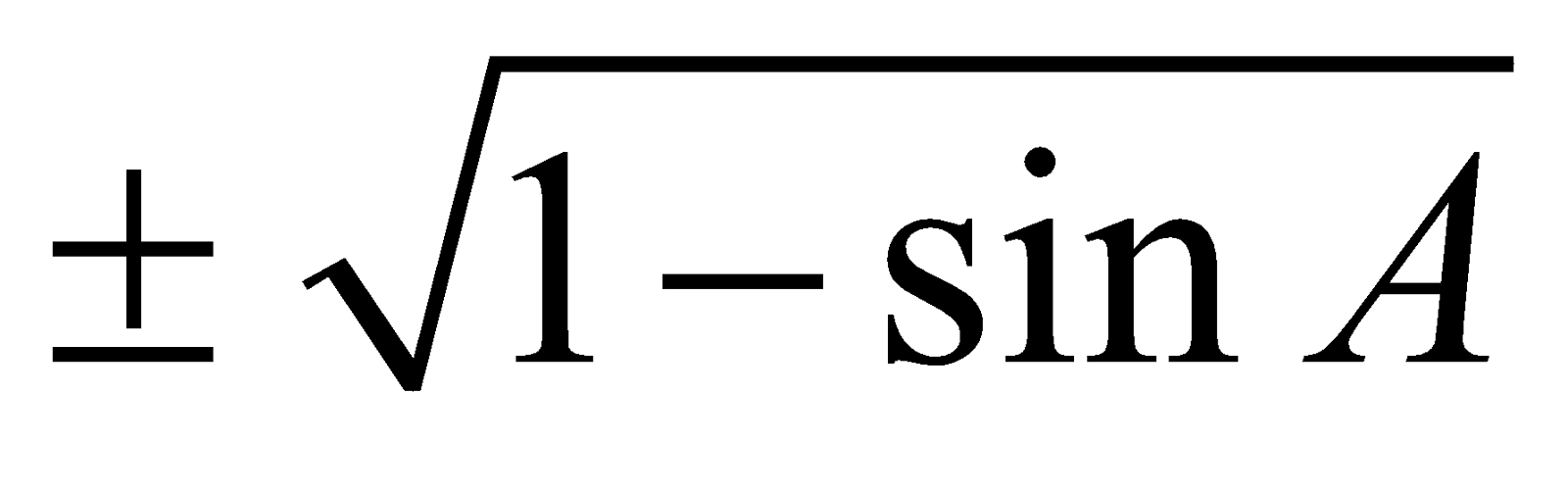
By adding and subtracting, we have
2 sin =
=  ...(i)
...(i)
and 2 cos  =
= 
 ...(ii)
...(ii)
In each of the formulae (i) and (ii) there are two ambiguous signs.
To find these ambiguities we proceed as follows :
We have, sin  + cos
+ cos  =
= 
The RHS of this equation is positive if
i.e. if, 
Hence 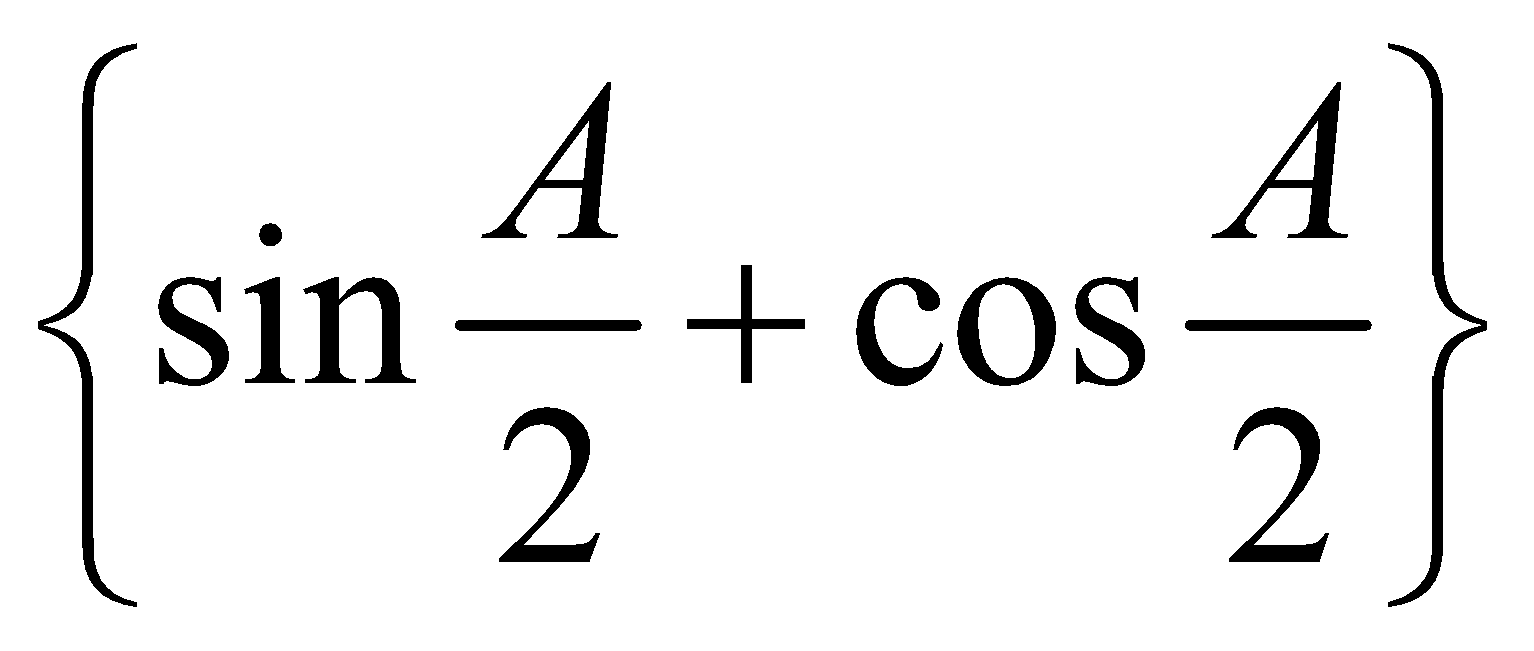 is positive if
is positive if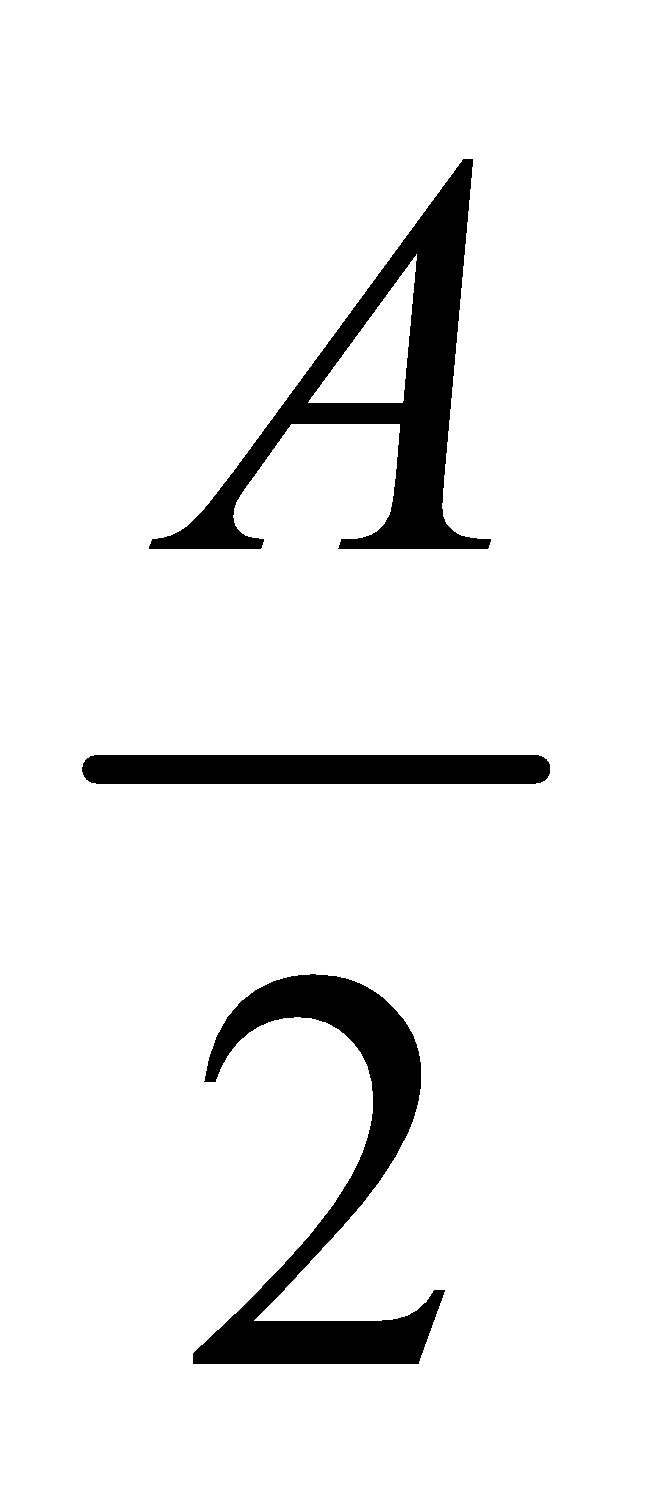 lies between
lies between  and
and  and it is negative otherwise.
and it is negative otherwise.
Similarly, 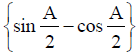 is positive if lies between and and otherwise it is negative.
is positive if lies between and and otherwise it is negative.
These results can be shown graphically as given in the following figure :
PERIODIC FORM OF a sinθ + b cosθ AND MINIMUM AND MAXIMUM VALUES
Let y = a sin θ + b cos θ. Put a = r cos α and b = r sinα then
y = r (sinθ cosα + cosθ sinα) = r sin (θ + α), where
Alternatively, if we put a = r sin β. b = r cos β, then
Now, consider 
We know that ;
; 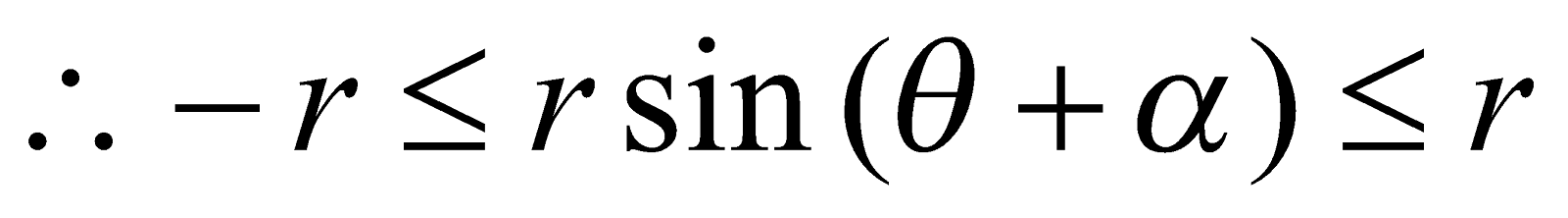
∴ Maximum value of  and Minimum value of
and Minimum value of 
Also, 
TO FIND THE SUM OF THE SINES OF A SERIES OF ANGLES, THE ANGLES BEING IN ARITHMETIC PROGRESSION
Let the angles be 
Let 
We have
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
and 

By adding together these n lines, we have
The other terms on the right -hand sides canceling one another.
Hence, we have
i.e., S 
TO FIND THE SUM OF THE COSINES OF A SERIES OF ANGLES, THE ANGLES BEING IN ARITHMETIC PROGRESSION
Let the angles be 

Let S ≡ cos α + cos (α + β) + cos (α + 2β) + ...... +
cos {α + (n – 1) β}
cos {α + (n – 1) β}
We have
. . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
and 
By adding together these n lines, we have
The other terms on the right-hand sides cancelling one another. Hence, we have
2S × sin = 2 cos
= 2 cos
i.e. S =







