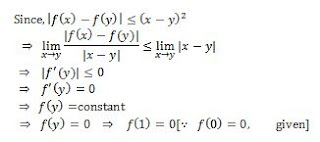Quiz-14 CONTINUITY AND DIFFERENTIABILITY

CONTINUITY AND DIFFERENTIABILITY-14

Dear Readers,

As per analysis for previous years, it has been observed that students preparing for JEE MAINS find Mathematics out of all the sections to be complex to handle and the majority of them are not able to comprehend the reason behind it. This problem arises especially because these aspirants appearing for the examination are more inclined to have a keen interest in Mathematics due to their ENGINEERING background. Furthermore, sections such as Mathematics are dominantly based on theories, laws, numerical in comparison to a section of Engineering which is more of fact-based, Physics, and includes substantial explanations. By using the table given below, you easily and directly access to the topics and respective links of MCQs. Moreover, to make learning smooth and efficient, all the questions come with their supportive solutions to make utilization of time even more productive. Students will be covered for all their studies as the topics are available from basics to even the most advanced. .

Q1. Let f is a real-valued differentiable function satisfying |f(x)-f(y) |≤(x-y)²,x,y ∈R and f(0)=0, then f(1) equals

•  1
•  2
•  0
•  -1

Solution

Q2. The function f(x)=x-|x-x²|,-1≤x≤1 is continuous on the interval

•  [-1,1]
•  (-1,1)
•  [-1,0)∪(0,1]
•  (-1,0)∪(0,1)

Solution

Q3. The function f(x)=x-|x-x²| is

•   Continuous at x=1
•  Discontinuous at x=1
•  Not defined at x=1
•  None of the above

Solution

Q4. The set of points where the function f(x)=|x-1| e^x is differentiable, is

•  R
•  R-{1}
•  R-{-1}
•  R-{0}

Solution
Since, |x-1| is not differentiable at x=1 

So, f(x)=|x-1| e^x is not differentiable at x=1 

Hence, the required set is R-{1}

Q5. If f(x) is continuous function and g(x) be discontinuous, then

•  f(x)+g(x) must be continuous
•  f(x)+g(x) must be discontinuous
•  f(x)+g(x) for all x
•  None of these

Solution
If possible, let f(x)+g(x) be continuous. Then, {f(x)+g(x)}-f(x) must be continuous ⇒g(x) must be continuous 

This is a contradiction to the given fact that g(x) is discontinuous 

Hence, f(x)+g(x) must be discontinuous

Q6. The value of k for which the function

is continuous at a=0, is

•  k=0
•  k=1
•  k=-1
•  None of these

Solution

Q7. The following functions are differentiable on (-1,2)

•  
  
  
  
•  
  
  
  
•  
  
  
  
•  None of these

Solution
Since the functions (log⁡t)² and sin⁡t/t are not defined on (-1,2). Therefore, the functions in options (a) and (b) are not defined on (-1,2) 

The function g(t)=(1-t+t²)/(1+t+t² ) is continuous on (-1,2) and 

f(x)=∫₀^x(1-t+t²)/(1+t+t²) dt is the integral function of g(t) 

Therefore, f(x) is differentiable on (-1,2) such that f' (x)=g(x)

Q8. Let f(x) be defined for all x>0 and be continuous. Let f(x) satisfy f(x/y)=f(x)-f(y) for all x,y and f(e)=1. Then,

•  f(x) is bounded
•  f(1/x)→0 as x→0
•  xf(x)→1 as x→0
•  f(x)=ln⁡x

Solution
We have, 

log⁡(x/y)=log⁡x-log⁡y and log⁡(e)=1 

∴f(x)=log⁡x 

Clearly, f(x) is unbounded because f(x)→-∞ as x→0 and f(x)→+∞ as x→∞ 

We have, f(1/x)=log⁡(1/x)=-log⁡x 

As x→0,f(1/x)→∞ Also, 

Q9.

•  f(x) is continuous at x=2
•  f(x) is continuous but not differentiable at x=2
•  f(x) is everywhere differentiable
•  The right derivative of f(x) at x=2 does not exist

Solution

Q10. Define f on R into itself by 

•  f is continuous at 0 but not differentiable at 0
•  f is both continuous and differentiable at 0
•  f is differentiable but not continuous at 0
•  None of the above

Solution