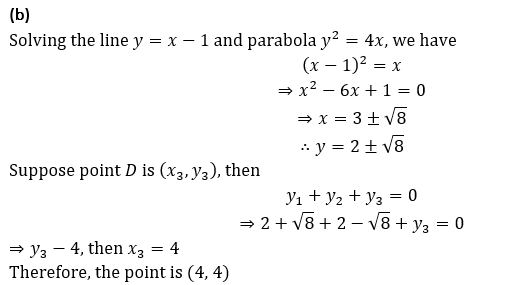Conic Section Quiz-18

Conic Section Quiz-18

Dear Readers,

In JEE exams, Conic section is one of the most important topic of Mathematics that comes under Coordinate Geometry, it has total of 15 percent weightage out of which 6% questions are asked in JEE mains and 9% in Advance.

Q1. An equilateral triangle SAB is inscribed in the parabola y²=4ax having its focus at ‘S'. If chord AB lies towards the left of S, then side length of this triangel is

•  2a(2-√3)
•  4a(2-√3)
•   a(2-√3)
•  8a(2-√3)

Solution

Q2. If α-β= constant, then the locus of the point of intersection of tangents at P(a cos⁡α,bsin⁡α ) and Q(a cos⁡β,b sin⁡β ) to the ellipse x²/a² +y²/b² =1 is

•  A circle
•  A straight line
•  An ellipse
•  A parabola

Solution

Q3. A straight line I_1 with equation x-2y+10=0 meets the circle with equation x²+y²=100 at B in the first quadrant. A line through B, perpendicular to l1 cuts y-axis at P(0,t). The value of ‘t’ is

•  12
•  15
•  20
•  25

Solution

Q4.   If the equation of any two diagonals of a regular pentagon belongs to family of lines (1+2λ)y-(2+λ)x+1-λ=0 and their lengths are sin⁡36°, then locus of centre of circle circumscribing the given pentagon (the triangles formed by these diagonals with sides of pentagon have no side common) is

•  x²+y²-2x-2y+1+sin²72°=0
•  x²+y²-2x-2y+cos²⁡72°=0
•  x²+y²-2x-2y+1+cos²72°=0
•  x²+y²-2x-2y+sin²72°=0

Solution

Q5. If the line x-1=0 is the directrix of the parabola y²-kx+8=0, then one of the values of k is

•  1/8
•  8
•  4
•  1/4

Solution

Q6. The length of the major axis of the ellipse (5x-10)²+(5y+15)²=(3x-4y+7)²/4 is

•  10
•  20/3
•  20/7
•  4

Solution

Q7. If the circumference of the circle x²+y²+8x+8y-b=0 is bisected by the circle x²+y²-2x+4y+a=0, then a+b equals to

•  50
•  56
•  -56
•  -34

Solution

Q8. The line x-y=1 intersects the parabola y²=4x at A and B. Normals at A and B intersect at C. If D is the point at which line CD is normal to the parabola, then coordinates of D are

•  (4,-4)
•  (4, 4)
•  (-4,-4)
•  None of these

Solution

Q9.The locus of a point which moves such that the sum of the squares of its distance from three vertices of a triangle is constant is a/an

•  Circle
•  Straight line
•  Ellipse
•  None of these

Solution

Q10.A circle with centre (a,b) passes through the origin. The equation of the tangent to the circle at the origin is

•  ax-by=0
•  ax+by=0
•  bx-ay=0
•  bx+ay=0