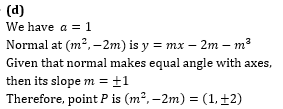Conic Section Quiz-32

Conic Section Quiz-32

Dear Readers,

In JEE exams, Conic section is one of the most important topic of Mathematics that comes under Coordinate Geometry, it has total of 15 percent weightage out of which 6% questions are asked in JEE mains and 9% in Advance.

Q1.  The point of intersection of the tangents of the parabola y^2=4x, drawn at end points of the chord x+y=2 lies on

•   x-2y=0
•   x+2y=0
•   y-x=0
•   x+y=0

Solution

Q2.  If the eccentricity of the hyperbola x^2-y^2 sec^2 α=5 is √3 times the eccentricity of the ellipse x^2 sec^2 α+y^2=25, then a value of α is

•  π/6
•  π/4
•  π/3
•  π/2

Q3.  Tangents are drawn to the circle x^2+y^2=1 at the points where it is met by the circles, x^2+y^2=(λ+6)x+(8-2λ)y-3=0,λ being the variable. The locus of the point of intersection of these tangents is

•   2x-y+10=0
•   x+2y-10=0
•   x-2y+10=0
•   2x+y-10=0

Solution

Q4.    At what point on the parabola y^2=4x the normal makes equal angle with axes?

•   (4, 4)
•   (9, 6)
•   (4,-4)
•   (1,±2)

Solution

Q5.  The angle between the tangents to the parabola y^2=4ax at the points where it intersects with the line x-y-a=0 is

•  π/3
•  π/4
•  π/6
•  π/2

Solution

Q6.  Let ABCD be a quadrilateral with are 18, with side AB parallel to the side CD and AB=2CD. Let AD be perpendicular to AB and CD. If a circle is drawn inside the quadrilateral ABCD touching all the side, then its radius is

•   3
•   2
•   3/2
•   1
Solution

Q7.  min [(x_1-x_2 )^2+(5+√(1-x_1^2 )-√(4x_2 ))^2 ]∀ x_1,x_2∈R is

•   √5+1
•   4√5-1
•  √5+1
•   √5-1

2x^2-2y^2+5xy+5=0

Q8.  The locus of the vertex of the family of parabolas y=(a^3 x^2)/3+(a^2 x)/2-2a is

•  xy=105/64
•  xy=3/4
•  xy=35/16
•  xy=64/105

Solution

Q9. The two circles which passes through (0,a) and (0,-a) and touch the line y=mx+c will intersect each other at right angle, if

•   a^2=c^2 (2m+1)
•   a^2=c^2 (2+m^2 )
•   c^2=a^2 (2+m^2 )
•   c^2=a^2 (2m+1)

Solution

Q10. If the normals to the parabola y^2=4ax at the ends of the latus rectum meet the parabola at Q,Q', then QQ' is

•  10a
•  4a
•  20a
•  12a

Solution