Permutations and Combinations-Quiz-2

Permutations and Combinations Quiz-2

Dear Readers,

Permutations and Combinations is one of the most important chapters of Algebra in the JEE syllabus and other engineering exams. For JEE Mains, it has 4% weightage and for JEE Advanced, it has 5% weightage..

Q1. The number of ways in which we can get a score of 11 by throwing three dice is

•  5!
•  2(5!)
•  10!
•  1/2 x 10!

Solution
Two positions for A₁ and A₁₀ can be selected in ¹⁰C₂ ways. Rest 8 students can be ranked in 8! ways. Hence total number of ways is ¹⁰C₂ X 8! = (1/2)(10!)

Q2.Among 10 persons, A,B,C are to speak at a function. The number of ways in which it can be done if A wants to speak before B and B wants to speak before C is

•  10!/24
•  9!/6
•  10!/6
•  None of these

Solution
Places for A,B,C can be chosen in ¹⁰C₃ ways. Remaining 7 persons can speak in 7! ways. Hence, the number of ways in which they can speak is ¹⁰C₃ X 7! = 10!/6

Q3.  A team of four students is to be selected from a total of 12 students. The total number of ways in which the team can be selected such that two particular students refuse to be together and other two particular students which to be together only is equal to

•  220
•  182
•  226
•  None of these

Solution
Let S₁ and S₂ refuse to be together and S₃ and S₄ want to be together only. The total number of ways when S₃ and S₄ are selected is (⁸C₂ + ⁸C₁) = 44. The total ways when S₃ and S₄ are not selected is (⁸C₄ + ²C₁ X ⁸C₃). Thus, the total number of ways is 44 + 182 = 226

Q4. The number of nine-non-zero digits such that all the digits in the first four places are less than the digit in the middle and all the digits in the last four places are greater than that in the middle is

•  2(4!)
•  3(7!)/2
•  2(7!)
•  ⁴P₄ X ⁴P₄

Solution

Q5.Messages are conveyed by arranging four white, one blue and three red flags on a pole. Flags of the same colour are alike. If a message is transmitted by the order in which the colours are arranged, the total number of messages that can be transmitted if exactly six flags are used is

•  45
•  65
•  125
•  185

Solution

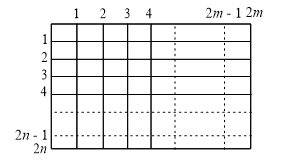
Q6. A rectangle with sides and is divided into squares of unit length by drawing parallel lines as shown in the diagram, then the number of rectangles possible with odd side lengths is

•  (m + n - 1)²
•  4^m+n-1
• m²n²
•  m(m + 1)n(n + 1)

Solution

Q7.The number of triangles that can be formed with 10 points as vertices, n of them being collinear, is 110. Then n is

•  3
•  4
•  5
•  6

Solution

Q8.If all the permutations of the letters in the word ‘OBJECT’ are arranged (and numbered serially) in alphabetical order as in a dictionary, then the 717^th word is

•  TOJECB
•  TOEJBC
•  TOCJEB
•  TOJCBE

Solution
The order of letters of the words ‘OBJECT’ is B C E J O T
Words starting with B can be formed in 5! Ways.
Words starting with C can be formed in 5! Ways.
Words starting with E can be formed in 5! Ways.
Words starting with J can be formed in 5! Ways.
Words starting with O can be formed in 5! Ways.
Words starting with TB can be formed in 4! Ways.
Words starting with TC can be formed in 4! Ways.
Words starting with TE can be formed in 4! Ways.
Words starting with TJ can be formed in 4! Ways.
Words starting with TOB can be formed in 3! Ways.
Words starting with TOC can be formed in 3! Ways.
Words starting with TOE can be formed in 3! Ways.
Words starting with TOJB can be formed in 2! Ways.
Words starting with TOJC can be formed in 2! Ways.
Therefore, the total number of words is 718 words. Hence 717th word is TOJCBE

Q9.The maximum number of points of intersection of five lines and four circles iss

•  60
•  72
•  62
•  None of the above

Solution

Q10. The number of different seven digit numbers that can be written using only the three digits 1,2 and 3 with the condition that the digit 2 occurs twice in each number is

•  ⁷P₂2⁵
•  ⁷C₂2⁵
•  ⁷P₂5²
• None of these

Solution
Other than 2, remaining five places can be filled by 1 and 3 for each place. The number of ways for five places is 2 x 2 x 2 x 2 x 2 = 2⁵. For 2, selecting 2 places out of 7 is ⁷C₂. Hence, the required number of ways is ⁷C₂ X 2⁵