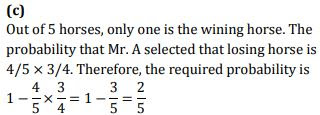Probability-Quiz-9

Probability Quiz-9

Dear Readers,

Probability is an important topic in JEE advanced examination. In this exam, probability carries weightage of 7% of questions. With focused practice good marks can be fetched from this topic .

Q1. A cricket club has 15 members, of whom only 2 can bowl. If the names of 15 members are put into a box and 11 are drawn at random, then the probability of getting an eleven containing at least 3 bowlers is:

•  7/13
•  6/13
•  11/15
•  12/13

Solution

Q2.One ticket is selected at random from 100 tickets numbered 00, 01,02, …, 98, 99. If x_1 and x_2 denotes the sum and product of the digits on the tickets, then P(x₁=9/x₂=0) is equal to:

•  2/19
•   19/100
•  1/50
•  None of these

Solution

Q3.  The numbers (a,b,c) are selected by throwing a dice thrice, then the probability that (a,b,c) are in A.P.is:

•  1/12
•  1/6
•  1/4
•  None of these

Solution

Q4. A letter is known to have come either from LONDON or CLIFTON; on the postmark only the two consecutive letters ON are legible. The probability that if came from LONDON is:

•  1/17
•  12/17
•  17/30
•  3/5

Solution

Q5. A dice is thrown six times, it being known that each time a different digit is shown. The probability that a sum of 12 will be obtained in the first three throws is:

•  5/24
•  25/216
•  3/20
•  1/12

Solution

Q6. If the papers of 4 students can be checked by any one of the 7 teachers, then the probability that all the 4 papers are checked by exactly 2 teachers is:

•  2/7
•  12/49
• 32/343
•  None of these

Solution

Q7. On a Saturday night, 20% of all drivers in U.S.A. are under the influence of alcohol. The probability that a driver under the influence of alcohol will have an accident is 0.001. The probability that a sober driver will have an accident is 0.0001.If a car on a Saturday night smashed into a tree, the probability that the driver was under the influence of alcohol is:

•  3/7
•  4/7
•  5/7
•  6/7

Solution

Q8. Five horses are in a race. Mr. A selects two of the horses at random and bets on them. The probability that Mr. A selected the winning horse is:

•  3/5
•  1/5
•  2/5
•  4/5

Solution

Q9.Let p,q be chosen one by one from the set {1,√2,√3,2,e,π} with replacement. Now a circle is drawn taking (p,q) as its centre. Then the probability that at the most two rational points exist on the circle is (rational points are those points whose both the coordinates are rational):

•  2/3
•  7/8
•  8/9
•  None of these

Solution

Q10. There are 3 bags. Bag 1 contains 2 red and a^2-4a+8 black balls, bag 2 contains 1 red and a²-4a+9 black balls and bag 3 contains 3 red and a²2-4a+7 black balls. A ball is drawn at random from at random chosen bag. Then the maximum value of probability that is a red ball is:

•  1/3
•  1/2
•  2/9
• 4/9

Solution