STATES OF MATTER Quiz-17

STATES OF MATTER QUIZ-17

Dear Readers,

IIT JEE exam which consists of JEE Main and JEE Advanced is one of the most important entrance exams for engineering aspirants. The exam is held for candidates who are aspiring to pursue a career in the field of engineering and technical studies. Chemistry is important because everything you do is chemistry! Even your body is made of chemicals. Chemical reactions occur when you breathe, eat, or just sit there reading. All matter is made of chemicals, so the importance of chemistry is that it's the study of everything.

Q1. Two flasks A and B have equal volume. A is maintained at 300 K and B at 600 K. WhileA contains H₂ gas, B has an equal mass of CH₄ gas. Assuming ideal behaviours for both the gases, answer the following:

  Flask containing greater number of molecules

•  A
•  B
•  Both A and B
•  None

Solution:

Q2. The van der Waals constant for gases A,B, and C are as follows:
Gas a(dm⁶ kPa mol^-2) b(dm³ mol^-1) A 405.3 0.027 B 1215.9 0.030 C 607.95 0.032 Answer the following:

Which gas has the highest critical temperature?

•  A
•  B
•  C
•  None

Solution:

Q3.  For the given ideal gas equation PV=nRT, answer the following questions:

   In the above equation, the value of universal gas constant depends only upon

•  The nature of the gas
•  The pressure of the gas
•  The temperature of the gas
•  The units of measurement

Solution:

Q4.  Using van der Waals equation (P+a/V²)(V-b)=RT, answer the following equations:

   The van der Waals equation explains the behaviour of

•  Ideal gases
•  Real gases
•  Vapours
•  Non-real gases

Solution:

Q5. Compressibility factor Z=PV/RT. Considering ideal gas, real gas, and gases at critical state, answer the following questions:

   The compressibility factor of an ideal gas is

•  0
•  1
•  2
•  3

Solution:

Q6. Two gaseous molecules A and B are traveling towards each other. Let the mean free path of the molecule be σ and Z be the collision number with other molecules at pressure 1 atm. Answer the following questions

  The free path of a gas molecule is the distance

•  Between the two opposite walls of the container
•  That molecules travel in the second
• Through which a molecule moves between two successive collisions
•  None of these

Solution:

Q7. The constant motion and high velocities of gas particles lead to some important practical consequences. One such consequence is that gases mix rapidly when they come in contact. Take the stopper off a bottle of perfume, for instance, and the odour will spread rapidly through the room as perfume molecules mix with the molecules in the air. This mixing of different gases by random molecular motion and with frequent collision is called diffusion. A similar process in which gas molecules escape without collision through a tiny hole into a vaccum is called effusion. Both the processes follow Graham’s law which is mathematically put as r ∝ √1/d. The average distance travelled by molecules between successive collisions is called mean free path.

Answer the following questions on the basis of the above information:

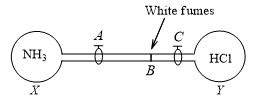
The stopcocks of the bulbs X (containing NH₃) and Y (containing HCl), both under identical conditions, are opened simultaneously. White fumes of NH₄Cl, are formed at point B. If AB =36.5 cm, then BC is approximately

•  18.0 cm
•  25.0 cm
•  20.0 cm
•  36.5 cm

Solution:

Q8. The behaviour of ideal gas is governed by various gas laws which are described by mathematical statements as given below:

1. PV=k (constant) at constant n and T
2. V⁄T = k₂ (constant) at constant n and P
3. V⁄n = k₃ (constant) at constant T and P
4. PV = nRT
5. P⁄T = k₄(constant) at constant n and V Answer the following
The value of k₂ is

•  Independent of nature and amount of gas
•  Depends on temperature and pressure conditions
•  Depends on pressure and amount of gas
•  Depends only on nature of gas

Solution:

Q9.Consider the adjacent diagram. Initially, flask A contained oxygen gas at 27℃ and 950 mm of Hg, and flask B contained neon gas at 27℃ and 900 mm. Finally, two flask were joined by means of a narrow tube of negligible volume equipped with a stopcock and gases were allowed to mixup freely. The final pressure in the combined system was found to be 910 mm of Hg

Which of the following statements concerning oxygen and neon gas is true in the beginning, when the stopcock was just opened?

•  O₂ moved at faster rate toward flask B
•  Ne moved at faster rate towards flask A
•  Both O₂ and Ne gases moves at equal rate
•  Insufficient information to compare the rate of effusion

Solution:

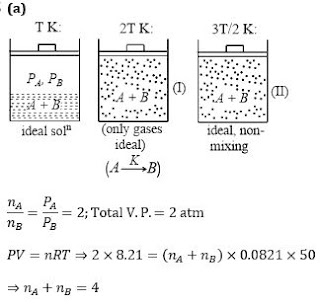
Q10.  The system shown in the figure is in equilibrium, where A and B are isomeric liquids and form an ideal solution at T K. Standard vapour pressures of A and B are P⁰_A and P⁰_B , respectively, at T K. We collect the vapour of A and B in two containers of volume V, first container is maintained at 2 T K and second container is maintained at 3T⁄2. At the temperature greater than T K, both A and B exist in only gaseous form,
We assume than collected gases behave ideally at 2 T K and there may take place an isomerization reaction in which A gets converted into Bby first-order kinetics reaction given as:

where k is a rate constant.
In container (II) at the given temperature 3T/2, A and B are ideal in nature and non reacting in nature. A small pin hole is made into container. We can determine the initial rate of effusion of both gases in vacuum by the expression

 r=K∙P/√M₀ Where, P=pressure difference between system and surrounding K=positive constant M₀=molecular weight of the gas

 If partial vapour pressure of A is twice that of partial vapour pressure of B and total pressure 2 atm at T K, where T=50 K and V=8.21 L, then the number of moles of A and B in vapour phase is:

•  8/3 , 4/3
•  4/3 , 1/3
•  2/3 , 1/4
•  10/3 , 4/3

Solution: