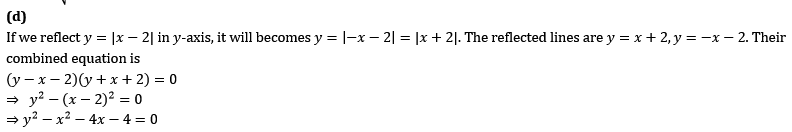Straight Lines-Quiz-11

Straight Lines Quiz-11

Dear Readers,

The unit Straight Line holds sheer significance in the JEE Advanced and other engineering exams. It has a weightage of 6% pairing with Circles. With focused practice good marks can be fetched from this section. These questions are important in achieving your success in JEE and Other Engineering Exams..

Q1. Given A≡(1,1) and AB is any line through it cutting the x-axis in B. If AC is perpendicular to AB and meets the y-axis in C, then the equation of locus of midpoint P of BC is

•  x+y=1
•  x+y=2
•  x+y=2xy
•  2x+2y=1

Solution

Q2. In a trinagle ABC,A≡(α,β),B≡(2,3) and C≡(1,3) and point A lies on line y=2x+3 where α∈I. Area of ∆ABC,∆, is such that [∆]=5. Possible coordinates of A are (where [.] represents greatest integer function)

•  (2, 3)
•  (5, 13)
•  (-5,-7)
•  (-3,-5)

Solution

Q3. Two vertices of a triangle are (4,-3) and (-2,5). If the orthocentre of the triangle is at (1, 2), then the third vertex is

•  (-33,-26)
•  (33, 26)
•  (26, 33)
•  None of these

Solution

Q4. The line x/3+y/4=1 meets the y-axis and x-axis at A and B, respectively. A square ABCD is constructed on the line segment AB away from the origin. The coordinates of the vertex of the square farthest from the origin are

•  (7, 3)
•  (4, 7)
•  (6, 4)
•  (3, 8)

Solution

Q5. The distance between the two parallel lines is 1 unit. A point 'A' is chosen to lie between the lines at a distance 'd' from one of them. Triangle ABC is equilateral with B on one line and C on the other parallel line. The length of the side of the equilateral triangle is

•  
•  
•  
•  

Solution

Q6. The combined equation of straight lines that can be obtained by reflecting the lines y=|x-2| in the y-axis is

•  y²+x²+4x+4=0
•  y²+x²-4x+4=0
•  y²-x²+4x-4=0
•  y²-x²-4x-4=0

Solution

Q7. In ∆ABC the coordinates of the vertex A are (4,-1) and lines x-y-1=0 and 2x-y=3 are internal bisectors of angles B and C. Then, radius of incircle of triangle ABC is

•  4/√5
•  3/√5
•  6/√5
•  7/√5

Solution

Q8. θ₁ and θ₂ are the inclination of lines L₁ and L₂ with x-axis. if L₁ and L₂ pass through p(x₁,y₁ ), then equation of one of the angle bisector of these lines is

•  
•  
•  
•  

Solution

Q9. OPQR is a square and M,N are the midpoints of the sides PQ and QR, respectively. If the ratio of the areas of the square and the triangle OMN is λ:6, then λ/4 is equal to

•  2
•  4
•  2
•  16

Solution

Q10. Consider 3 lines as fallows
L₁:5x-y+4=0
L₂:3x-y+5=0
L₃:x+y+8=0
If these lines enclose a triangle ABC and sum of the squares of the tangent to the interior angles can be expressed in the form p/q where p and q are relatively prime numbers, then the value of p+q is

•  500
•  450
•  230
•  465

Solution