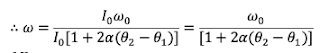Thermal Properties of Matter-Quiz-10

 

THERMAL PROPERTIES OF MATTER QUIZ-10

Dear Readers,

JEE Advanced Physics Syllabus can be referred by the IIT aspirants to get a detailed list of all topics that are important in cracking the entrance examination. JEE Advanced syllabus for Physics has been designed in such a way that it offers very practical and application-based learning to further make it easier for students to understand every concept or topic by correlating it with day-to-day experiences. In comparison to the other two subjects, the syllabus of JEE Advanced for physics is developed in such a way so as to test the deep understanding and application of concepts.

Q91. A glass cylinder container m_0=100 g of mercury at a temperature of t_0=0°C. When temperature becomes t_1=20°C the cylinder contains m_1=99.7 g of mercury. The coefficient of volume expansion of mercury y_He=18×10^(-5)/°C. Assume that the temperature of the mercury is equal to that of the cylinder. The coefficient of linear expansion of glass a is

•  10^(-5)/°C
•  2×10^(-5)/°C
•  3×10^(-5)/°C
•  6×10^(-5)/°C

Solution

92. A glass vessel is filled up to 3/5th of its volume by mercury. If the volume expansivities of glass and mercury be 9×10^(-6)/°C and 18×10^(-5)/°C, respectively, then the coefficient of apparent expansion of mercury is

•  17.1×10^(-5)/°C
•  9.9×10^(-5)/°C
•  17.46×10^(-5)/°C
•  16.5×10^(-5)/°C

Solution

Q93. An iron ball (coefficient of linear expansion =1.2×10^(-5)/°C) has a diametA steel ball of mass m_1=1 kg moving with velocity 50 m/s collides with another ball of mass m_2=200 g lying on the ground. During the collision their internal energies change equally and T_1and T_2 are the rise in temperature of masses m_1and m_2, respectively. If specific heat of steel is 0.105 and J=4.18 J/cal, then

•   T_1=7.1°C and T_2=1.47°C
•  T_1=1.47°C and T_2=7.1°C
•  T_1=3.4 K and T_2=17.0 K
•  T_1=7.1 K and T_2=1.4 K

Solution

Q94. A wire is made by attaching two segments together end to end. One segment is made of aluminium and the other is steel. The effective coefficient of linear expansion of the two segment wire is 19×10^(-6)/(°C). The fraction length of aluminium is (linear coefficients of thermal expansion of aluminium and steel are 23×10^(-6) (°C) and 12×10^(-6)/(°C), respectively

•  5/11
•  6/11
•  7/11
•  8/11

Solution

Q95. A cooking vessel on a slow burner contains 5 kg of water and an unknown mass of ice in equilibrium at 0°C at time t=0. The temperature of the mixture is measured at various times and the result is plotted as shown in Figure. During the first 50 min the mixture remains at 0°C. From 50 min to 60 min, the temperature increases to 2°C. Neglecting the heat capacity of the vessel, the initial mass of the ice is

•  10/7 kg
•  5/7 kg
•  5/4 kg
•  5/8 kg

Solution
 

Q96. Ice at 0°C is added to 200 g of water initially at 70°C in a vacuum flask. When 50 g of ice has been added and has all melted, the temperature of flask and contents is 40°C. When a further 80 g of ice is added and has all melted, the temperature of whole becomes 10°C. Neglecting heat lost to surrounding the latent heat of fusion of ice is

•  80 cal/g
•  90 cal/g
• 70 cal/g
•  540 cal/g

Solution

Q97. A body cools from 50°C to 49°C in 5 s. How long will it take to cool from 40°C to 39.5°C? assume the temperature of surroundings to be 30°C and Newton’s law of cooling to be valid

•  2.5 s
•  10 s
•  20 s
•  5 s

Solution
97 (b) According to Newton’s law of cooling, the ratio of cooling is directly proportional to the temperature difference. When the average temperature difference is halved, the rate of cooling is also halved. So, the time taken is 10 s

Q98. A uniform brass disc of radius a and mass m is set into spinning with angular speed ω_0 about an axis passing through centre of disc and perpendicular to the plane of disc. If its temperature increases from θ_1°C to θ_2°C without disturbing the disc, what will be its new angular speed? (The coefficient of linear expansion of brass is α

•  ω_0 [1+2a(θ_2-θ_1)]
•  ω_0 [1+a(θ_2-θ_1)]
•  ω_0/([1+2α(θ_2-θ_1)])
•  None of these

Solution

Q99. Two elastic rods are joined between fixed supports as shown in Figure. Condition for no change in the lengths of individual rods with the increase of temperature (α_1,α_2=linear expansion coefficient, A_1,A_2= area of rods, y_1,y_2=Young’s modulus) is

•  A_1/A_2 =(α_1 y_1)/(α_2 y_2 )
•  A_1/A_2 =(L_1 α_1 y_1)/(L_2 α_2 y_2 )
•  A_1/A_2 =(L_2 α_2 y_2)/(L_1 α_1 y_1 )
•  >A_1/A_2 =(α_2 y_2)/(α_1 y_1 )

Solution

Q100. A bucket full of hot water cools from 75°C to 70°C in time T_1, from 70°C to 65°C in time T_2 and from 65°C to 60°C in time T_3, then

•  IT_1=T_2=T_3
•  T_1>T_2>T_3
•  T_1
• T_1>T_2

Solution
100 (c) According to Newton’s law of cooling the rate of cooling depends upon the difference of temperature between the body and the surrounding. It means that when the difference of temperature between the body and the surrounding is small, time required for same fall in temperature is more in comparison with the same fall at higher temperature difference between the body and surrounding. So according to problem T_1