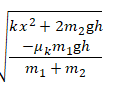Work power energy is the most important chapter when it comes to mechanics, for JEE (Advanced). The chapter is quite tricky and takes a lot of time and devotion on your part to understand and master. But this chapter is a complete gold medal for almost all the questions of the mechanics can be solved by the work power energy approach if you master this topic..
Q1.In a conservative force field, we can find the radial component of force F from the potential energy function (U) using the relation F=dU/dr. Positive value of F mean repulsive forces and vice-versa. We can find the equilibrium position, where force is zero. We can also calculate ionisation energy, which is the work done to move the particle from a certain position to infinity.
Let us consider a particle bound to a certain point at a distance r from the centre of the force. The potential energy function of the particle is given by U (r)=A/r^2 -B/r, where A and B are positive constants
The nature of equilibrium is
Q2.Two unequal masses are tied together with a cord with a compressed spring in between
When the cord is burnt with a match releasing the spring, the two masses fly apart with equal
Q3. A body of mass 2 kg starts from rest and moves with uniform acceleration. It acquires a velocity 20 ms^(-1) in 4 s
The power exerted on the body at 2 s is
Solution
v=u+at ⇒20=0+a×4 ⇒a=5 ms^(-2)
F=ma=2×5=10 N
Velocity at 2 s:v_1=at=5×2=10 ms^(-1)
Power =Fv_1=10×10=100 W
v=u+at ⇒20=0+a×4 ⇒a=5 ms^(-2)
F=ma=2×5=10 N
Velocity at 2 s:v_1=at=5×2=10 ms^(-1)
Power =Fv_1=10×10=100 W
Q4.
Sand particles drop vertically at the rate of 2 kgs^(-1) on a conveyor belt moving horizontally with a velocity of 0.2 ms^(-1)
The extra force required to keep the belt moving is
Q5.A ladder of length l carrying a man of mass m at its end is attached to the basket of a balloon of massM. The entire system is in equilibrium in the air. As the man climbs up the ladder into the balloon, the balloon descends by a height h
The potential energy of the man
The potential energy of the man
Solution
When the man climbs the ladder of length l, the balloon descends by height h. So net height gained by the man is l-h. Hence, gain in potential energy of the man is mg(l-h) Work done by man :W_1=mgl Inclination in potential energy of balloon= work done by man – increase in potential energy of man, i.e., mgl-mg(l-h)=mgh
When the man climbs the ladder of length l, the balloon descends by height h. So net height gained by the man is l-h. Hence, gain in potential energy of the man is mg(l-h) Work done by man :W_1=mgl Inclination in potential energy of balloon= work done by man – increase in potential energy of man, i.e., mgl-mg(l-h)=mgh
Q6.
A single conservation force F(x) acts on a 1.0 kg particle that moves along the x-axis. The potential energy U(x) is given by U(x)=20+(x-2)^2 where x is in meters. At x=5.0 m, the particle has a kinetic energy of 20 J
What is the mechanical energy of the system?
Solution
At x=5 m, U=20+(5-2)^2=29 J, K=20 J
Mechanical energy=E=U+K=29+20=49 J
Q7.A 1.5 kg block is initially at rest on a horizontal frictionless surface when a horizontal force in the positive direction of x-axis is applied to the block. The force is given by F ⃗=(4-x^2)i ̂ N, when x is in meter and the initial position of the block is x=0
The maximum kinetic energy of the block between x=0 and x=2.0 m is
Solution
Loss in PE of spring + loss in PE of m_2= gain in KE of (m_1+m_2 )+work done against friction
⇒
1/2 kx^2+m_2 gh=1/2 (m_1+m_2 ) v^2+μ_k m_1 gh
⇒
v=√((kx^2+2m_2 gh-2μ_k m_1 gh)/(m_1+m_2 ))